Posts
Showing posts from May, 2023
Posted by
Physics Vidyapith
Distinction between Spontaneous and Stimulated Emission of Radiation
- Get link
- Other Apps
Posted by
Physics Vidyapith
Absorption of all the energy of a incident photon by a free electron
- Get link
- Other Apps
Posted by
Physics Vidyapith
Minimum Energy Or Zero Point Energy of a Particle in an one dimensional potential box or Infinite Well
- Get link
- Other Apps

Posted by
Physics Vidyapith
Bohr's Theory of Hydrogen-Like Atoms
- Get link
- Other Apps
Posted by
Physics Vidyapith
Bohr's Model of Atom
- Get link
- Other Apps

Posted by
Physics Vidyapith
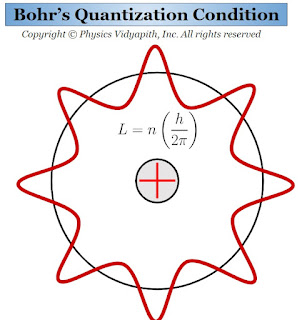
Bohr's Quantization Condition
- Get link
- Other Apps
Posted by
Physics Vidyapith
Drawbacks of Old Quantum Theory
- Get link
- Other Apps
Posted by
Physics Vidyapith
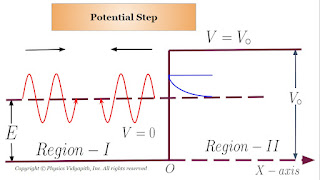
One dimensional Step Potential Barrier for a Particle
- Get link
- Other Apps
Posted by
Physics Vidyapith
Wave function of a particle in free state
- Get link
- Other Apps