Skip to main content

Search This Blog

Physics Vidyapith ✍️

(The Advance Learning Institute of Physics and Technology)

Home
Study Material
Test Series
Numericals & Solutions
Membership Form
About Us
Message Us
Disclaimer
Privacy Policies
Terms and Conditions

Posts

Showing posts from May, 2022

Posted by Physics Vidyapith

Displacement Current

Get link
Facebook
Twitter
Pinterest
Email
Other Apps

Posted by Physics Vidyapith

Mechanism of Flow of Charge in Metals: Free Electron Gas Theory

Get link
Facebook
Twitter
Pinterest
Email
Other Apps

Posted by Physics Vidyapith

Derivation of Ohm's Law

Get link
Facebook
Twitter
Pinterest
Email
Other Apps

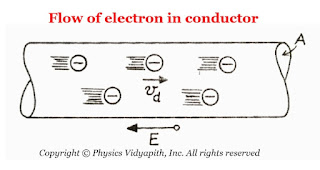
Posted by Physics Vidyapith

Relation between electric current and drift velocity

Get link
Facebook
Twitter
Pinterest
Email
Other Apps

Newer Posts Older Posts Home

Powered by Blogger

Theme images by Gintare Marcel

Study-Material

Electric Charge and its properties

Coulomb′s law and Application

Vector form of Coulomb′s Law

Force between multiple charges (Superposition principle of electrostatic forces)

Electric Line of Force and its Properties

Electric field Intensity (Definition) and Electric field Intensity due to point charge

Electric Dipole and Derivation of Electric field intensity at different points of an electric dipole

Derivation of torque on an electric dipole in an uniform and a non-uniform electric field

Electric potential and derivation of electric potential at a point due to point charged particle

Work done by a rotating electric dipole in uniform electric field

The electric potential at different points of the electric dipole

The electric potential energy of an electric dipole in the uniform electric field

The electric potential energy of a system of Charges

Gauss's Law for Electric Flux and Derivation

Electric field intensity due to point charge by Gauss's Law

Electric field Intensity due to a uniformly charged Spherical Shell

Electric field intensity due to the uniformly charged solid sphere(Conducting and Non-conducting)

Electric field intensity due to thick hollow non-conducting sphere

Electric field intensity due to uniformly charged plane sheet and parallel sheet

Electric field intensity due to uniformly charged wire of infinite length

Capacitance of an Isolated Spherical Conductor

Potential Energy of a Charged Conductor

Parallel Plate Air Capacitor and Its Capacitance

Capacitance of a Parallel Plate Capacitor Partly Filled with Dielectric Slab between Plates

Force between the plates of a Charged Parallel Plate Capacitor

Energy Stored in a Charged Capacitor

Description dielectric materials and their types

Relation between electric current and drift velocity

Derivation of Ohm's Law

Kirchhoff's laws for an electric circuits

Wheatstone's Bridge

Metre Bridge OR Slide Wire Bridge

Principle construction and working of potentiometer

Biot- Savart's Law

Motion of Charged Particles in Uniform Magnetic Field

Magnetic Field due to a Straight Current-Carrying Conductor of Finite Length

Ampere's circuital Law and its modification

Magnetic Field at the axis of a current-carrying circular loop

Magnetic Field at the center of a current-carrying circular loop

Principle, Construction and Working of Current Carrying Solenoid

Derivation of force on current carrying conductor in uniform magnetic field

Derivation of Force between two long and parallel current-carrying conductors

Magnetic Dipole Moment of Current carrying loop

Magnetic potential energy of current-loop in a magnetic field

Magnetic dipole moment of a revolving electron

Conversion of Galvanometer into an Ammeter

Diamagnetic substances and its properties

Paramagnetic substance and its properties

Mean Value and Root Mean Square Value of Alternating Current

Alternating Current Circuit containing Resistance only (R-Circuit)

Alternating Current Circuit containing Inductance only (L-Circuit)

Alternating Current Circuit containing Capacitance only (C-Circuit)

Circuit containing Inductor and Resistor in Series (L-R Series Circuit )

Circuit containing Capacitor and Resistor in Series (C-R Series Circuit )

Circuit containing Inductor and Capacitor in Series (L-C Series Circuit )

Circuit containing Inductor, Capacitor, and Resistor in Series (L-C-R Series Circuit )

Power in Alternating Current Circuit

Merits and Demerits of Alternating Current in Comparison to Direct Current

Faraday's Laws of Electromagnetic Induction

Self Induction and its Coefficient

Mutual Induction and its Coefficient

Classical world and Quantum world

Inadequacy of classical mechanics

Drawbacks of Old Quantum Theory

Bohr's Quantization Condition

Energy distribution spectrum of black body radiation

Energy distribution laws of black body radiation

The Compton Effect | Experiment Setup | Theory | Theoretical Expression | Limitation | Recoil Electron

Davisson and Germer's Experiment and Verification of the de-Broglie Relation

Significance of Compton's Effect

Assumptions of Planck’s Radiation Law

Derivation of Planck's Radiation Law

de-Broglie Concept of Matter wave

Definition and derivation of the phase velocity and group velocity of wave

Relation between group velocity and phase velocity ($V_{g}=V_{p}-\lambda \frac{dV_{p}}{d\lambda }$)

Group velocity is equal to particle velocity($V_{g}=v$)

Product of phase velocity and group velocity is equal to square of speed of light ($V_{p}.V_{g}=c^{2}$)

Heisenberg uncertainty principle

Generation of wave function for a free particle

Physical interpretation of the wave function

Derivation of time dependent Schrodinger wave equation

Derivation of time independent Schrodinger wave equation

Eigen Function, Eigen Values and Eigen Vectors

Postulate of wave mechanics or Quantum Mechanics

Quantum Mechanical Operators

Normalized and Orthogonal wave function

Particle in one dimensional box (Infinite Potential Well)

Minimum Energy Or Zero Point Energy of a Particle in an one dimensional potential box or Infinite Well

Normalization of the wave function of a particle in one dimension box or infinite potential well

Orthogonality of the wave functions of a particle in one dimension box or infinite potential well

Eigen value of the momentum of a particle in one dimension box or infinite potential well

Schrodinger's equation for the complex conjugate waves function

Probability Current Density for a free particle in Quantum Mechanics

Ehrenfest's Theorem and Derivation

Momentum wave function for a free particle

Wave function of a particle in free state

One dimensional Step Potential Barrier for a Particle

Inertial-frame and Non-inertial frame

Galilean Transformation Equations and Failure of Galilean Relativity

Derivation of Lorentz Transformation's Equations

Consequences of Lorentz's Transformation Equations

Concept of Simultaneity in Special Relativity

Derivation of Addition of Velocity in Special Relativity

Variation of Mass with Velocity in Relativity

Einstein’s Mass Energy Relation Derivation

Construction and Working of Nuclear Reactor or Atomic Pile

Nuclear Force and Its Properties

Work Energy Theorem Statement and Derivation

Conservative force and Non Conservative force

Conservation Law of linear momentum and its Derivation

Relation between angular velocity and linear velocity

Relation between angular acceleration and linear acceleration

Definition and Derivation of Centripetal Acceleration

Definition and Practical Applications of Centripetal Force

Motion of body in a vertical circle and its Practical Applications

Principle and Proof of Law of Conservation of Energy

Definition of work done and its essential condition

Force of Friction | Expression for the acceleration and the work done on inclined rough surface| Advantage and Disadvantage

Kepler's Laws of Planetary Motion

Newton's law for Gravitational Force

Deduction of Newton's Law of gravitation from Kepler's Law

Relation between gravitational acceleration and gravitational force

Gravitational field, Intensity of Gravitational field and its expression

Derivation of Gravitational Potential due to Point mass and on the Earth

Derivation of Gravitational Potential Energy due to Point mass and on the Earth

Expression for Orbital velocity of Satellite and Time Period

Variation of Acceleration Due to Gravity

Characteristics of Electromagnetic Wave

Displacement Current

Derivation of Maxwell first equation

Derivation of Maxwell's second equation

Derivation of Maxwell's third equation

Derivation of Maxwell's forth equation

Equation of continuity of electromagnetic wave

Equation of continuity for current density

Electromagnetic wave equation in free space

Solution of electromagnetic wave equations in free space

Transverse nature of electromagnetic waves

Electric and magnetic field vector are mutually perpendicular to each other in electromagnetic wave

Electromagnetic wave equation in non conducting media (i.e. Perfect dielectric or Lossless media)

Solution of electromagnetic wave equations in non conducting media

Electromagnetic Wave Equation in Conducting Media (i.e. Lossy dielectric or Partially Conducting)

Solution of electromagnetic wave equations in conducting media

Characteristic impedance of electromagnetic wave

Poynting Vector and Poynting Theorem

Energy flow in the electromagnetic wave in free space

Energy density in electromagnetic waves in free space

Momentum of electromagnetic wave

Radiation pressure of electromagnetic wave

Laser and properties of a Laser beam

Derivation of Einstein Coefficient Relation

Two Level Pumping in Laser

Three level pumping in Laser

Four level pumping in Laser

Application of Lasers

Brief Description of Liquid Lasers

Principle, Construction and Working of the Ruby Laser

Characteristics, Advantages, Disadvantages and Applications of Ruby Laser

Distinction between Spontaneous and Stimulated Emission of Radiation

Refraction of light and its Properties

Refraction of light through concave spherical surface

Refraction of light through convex spherical surface

Refraction of light through a thin lens Or Lens maker's formula

Combined focal length and power of two thin lenses in contact

Analytical expression of intensity for constructive and destructive interference due to Young's double slit

Interference of light due to thin film

Interference of light due to a wedge shaped thin film

Fringe width of wedge shaped thin film for normal incidence

Newton's rings in reflected monochromatic light

Difference between Fraunhofer and Fresnel diffraction

Fraunhofer diffraction due to a single slit

Fraunhofer diffraction due to a double slit

Missing Order in double slit diffraction pattern

Diffraction due to a plane diffraction grating or N- Parallel slits

Dispersive power of plane diffraction grating and its expression

Difference between interference and diffraction

Difference Between Prism Spectra and Grating Spectra

Numerical Aperture and Acceptance Angle of the Optical Fibre

Comparison of Single Mode and Multimode Index Fibres

Comparison of Step Index and Graded Index Fibres

Attenuation of optical signal in optical fibre

Principle of optical fibre communication

Principle of continuity in fluid

Bernoulli's Theorem and Derivation of Bernoulli's Equation

Principle, Construction and Working of Venturimeter

Viscosity, Viscous force and Coefficient of Viscosity

Difference between sound waves and light waves

Intensity of a wave

Bohr's Model of Atom

Bohr's Theory of Hydrogen-Like Atoms

Limitations of Bohr's Model

Laws of Photoelectric Emission

Failure of wave theory in explaining photoelectric emission effect

Einstein Photoelectric Emission

Basics and types of nanomaterials

Synthesis of Nanomaterials

Preparation of Nanostructured Particles By Sol-Gel Method

Nanoparticles and Its Properties

Comparison of Isothermal and Adiabatic Processes for an Ideal Gas

Concept of Perfect Gas

Kinetic theory of ideal gases

Superconductor and its properties

Blog Archive

August 20243
July 20242
May 20246
April 20242
March 20242
February 20247
January 20247
December 20238
November 202311
October 20234

August 20231
July 20232
June 20235
May 20239
April 20235
March 20234
February 202318
January 20239
December 202210
November 202216
October 202215
September 20221
August 20225
July 20224
June 20224
May 20224
April 202216
March 20227
February 202213
January 202230
December 20211
October 20211
August 20213

Show more Show less

Category

Alternating Current Circuits10
Atomic and Molecular Physics3
Biomedical1
Capacitors6
Classical Mechanics11
Current carrying loop in magnetic field4
Current Electricity10
Dielectric Materials1
Electromagnetic Induction3
Electromagnetic Wave Theory23

Electrostatic20
Gravitation11
Heat and Thermodynamics3
Kinematics Theory Of Gases2
Laser System & Application12
Magnetic Effect of Current9
Magnetic Substances2
Mechanical Properties of Fluids4
Nanoscience & Nanotechnology5
Nuclear Physics2
Numerical Problems and Solutions2
Optical Fibre5
Optics25
Photoelectric Effect3
Quantum Mechanics37
Relativity9
Superconductors1
Topic wise MCQ9
Waves2

Show more Show less

Follow Us

Facebook
Youtube
Instagram
Telegram
Whatsapp
Facebook page