Viscosity, Viscous force and Coefficient of Viscosity

Definition of Viscosity:

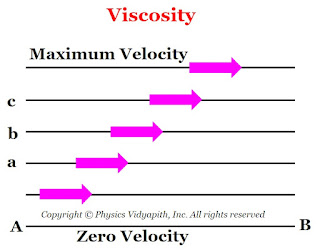
It is the property of a fluid that opposes the relative motion between its adjacent layers. This property of the fluid is known as viscosity. It is also called the resistance of fluid to flow or deformation or fluid thickness.

Effect of temperature on Viscosity:

The viscosity of the fluid decreases sharply with the temperature rise and becomes zero at boiling temperature. On the other hand, the viscosity of the gases increases with the temperature rise.

Definition of Viscous Force (Internal Frictional Force):

When a layer of fluid slide over another layer of the same fluid then an internal tangential frictional force act between them which opposes the relative motion between the layers. This tangential force is called viscous force or internal frictional force.

In the absence of external force, the viscous force would soon bring the fluid to rest.

Factor affecting the viscous force:

There are the following factors that affect the viscous force-

1.) The viscous force is directly proportional to the contact area of the layers. i.e.

$F \propto A \qquad(1)$

Where $A \rightarrow$ The contact area of the layers

2.) The viscous force is directly proportional to the velocity gradient between the layers. i.e.

$F \propto \frac{\Delta v_{x}}{\Delta z} \qquad(2)$

Where $\frac{\Delta v_{x}}{\Delta z} \rightarrow$ The velocity gradient that is shown in the figure below

From equation $(1)$ and equation $(2)$

$F \propto A \: \frac{\Delta v_{x}}{\Delta z}$

$F = \pm \: \eta \: A \: \frac{\Delta v_{x}}{\Delta z} \qquad(3)$

Where

$\eta \rightarrow$ It is a constant and also known as the "coefficient of viscosity" of the fluid.

$ \pm \rightarrow$ It indicates that the viscous force $F$ between two layers of fluid is a mutually interacting force. As shown above in figure (B), A layer that is just above layer $A$ exerts a force in the forward direction while a layer that is just below layer $A$ exerts an equal and opposite force i.e. in the backward direction.

Definition of Coefficient of Viscosity:

If $A=1$ and $\frac{\Delta v_{x}}{\Delta z} = 1$, then from equation $(3)$

$\eta = 1$

So from the above equation,  If the contact area and velocity gradient are units then the viscous force between the fluid is known as the coefficient of velocity.

Dimension of coefficient of viscosity:

$\left[ M L^{-1} T^{-1} \right]$

Unit of coefficient of viscosity:

$Kg-m^{-1}s^{-1}$

Here

$1 \: Kg-m^{-1}s^{-1} = 10\: poise = 1 \: decapoise$

Read More

Principle of continuity in fluid

Statement of Principle of Continuity:

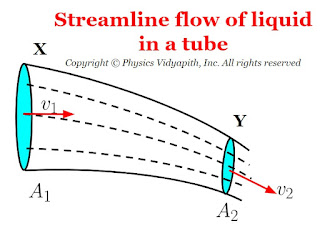
When an ideal liquid (i.e. incompressible and non-viscous liquid ) flows in streamlined motion through a tube of non-uniform cross-section, then the product of the velocity of flow and area of cross-section is always constant at every point in the tube.

Mathematical Analysis (Proof)

Let us consider, an ideal liquid (i.e. incompressible and non-viscous liquid ) flow in streamline motion through a tube $XY$ of the non-uniform cross-section.

Now Consider:

The Area of cross-section $X = A_{1}$

The Area of cross-section $Y = A_{2}$

The velocity per second (i.e. equal to distance) of fluid at cross-section $X = v_{1}$

The velocity per second (i.e. equal to distance) of fluid at cross-section $Y = v_{2}$

The volume of liquid entering at the cross-section $X$ in $1$ second is = $A_{1}v_{1}$

The mass of liquid entering at the cross-section $X$ in $1$ second is = $ \rho A_{1}v_{1}$

Similarly, the mass of the liquid coming out from the cross-section $Y$ in $1$ second is = $ \rho A_{2}v_{2}$

But the liquid which enters at cross-section $X$ must leave cross-section $Y$. Hence the masses are equal at both cross-section area, that is,

$\rho A_{1}v_{1} = \rho A_{2}v_{2} $

$ A_{1}v_{1} = A_{2}v_{2} $

$A v = constant$

Thus, the above equation shows that at every place in the tube, the product of the area of the cross-section of the tube and the velocity of the flow of the liquid is always the same. Therefore, the velocity of the liquid is smaller in the wider parts of the tube and larger in the narrow parts.

Read More

Principle, Construction and Working of Venturimeter

Principle of Venturimeter:

It is a device that is used for measuring the rate of flow of liquid through pipes. Its principle and working are based on Bernoulli's theorem and equation.

Construction:

It consists of two identical coaxial tubes $X$ and $Z$ connected by a narrow co-axial tube $Y$. Two vertical tubes $P$ and $Q$ are mounted on tubes $X$ and $Y$ to measure the pressure of the liquid that flows through pipes.. As shown in the figure below.

Working and Theory:

Connect this venturimeter horizontally to the pipe through which the liquid is flowing and note down the difference of liquid columns in tubes $P$ and $E$. Let the difference is $h$.

Let us consider that an incompressible and non-viscous liquid flows in streamlined motion through a tube $X$,$Y$, and $Z$ of the non-uniform cross-section.

Now Consider:

The Area of cross-section of tube $X$ = $A_{1}$
The Area of cross-section of tube $Y$ = $A_{2}$

The velocity per second (i.e. equal to distance) of fluid at the cross-section of tube $X$ = $v_{1}$
The velocity per second (i.e. equal to distance) of fluid at the cross-section of tube $Y$ = $v_{2}$

The Pressure of fluid at cross-section of tube $X$ = $P_{1}$
The Pressure of fluid at cross-section of tube $Y$ = $P_{2}$

Now the change in pressure on tube $P$ and $Q$:

$P_{1}-P_{2}=\rho g h \qquad(1)$

Where $\rho$ is the density of liquid.

According to the principle of continuity:

$A_{1} v_{1} = A_{2} v_{2} = \frac{m}{\rho}= V \qquad(2)$

Where $V$ is the volume of the liquid flowing per second through the pipe. Then from equation $(2)$

$\left.\begin{matrix} v_{1}=\frac{V}{A_{1}} \\ v_{2}=\frac{V}{A_{2}} \end{matrix}\right\} \qquad(3)$

Now apply Bernoulli's Theorem for horizontal flow (i.e $h_{1}=h_{2}$) in verturimeter.

$P_{1} + \frac{1}{2} \rho v_{1}^{2} = P_{2} + \frac{1}{2}\rho v_{2}^{2} $

$P_{1} - P_{2} = \frac{1}{2}\rho v_{2}^{2} - \frac{1}{2} \rho v_{1}^{2} $

$P_{1} - P_{2} = \frac{1}{2}\rho \left( v_{2}^{2} - v_{1}^{2} \right) \qquad(4) $

Now from equation $(1)$ and equation $(4)$, we get

$\rho g h = \frac{1}{2}\rho \left( v_{2}^{2} - v_{1}^{2} \right)$

$g h = \frac{1}{2} \left( v_{2}^{2} - v_{1}^{2} \right)$

Now substitute the value of $v_{1}$ and $v_{2}$ from equation $(3)$ in above equation

$g h = \frac{1}{2} \left( \frac{V^{2}}{A^{2}_{2}} - \frac{V^{2}}{A^{2}_{1}} \right)$

$g h = \frac{V^{2}}{2} \left( \frac{1}{A^{2}_{2}} - \frac{1}{A^{2}_{1}} \right)$

$g h = \frac{V^{2}}{2} \left( \frac{ A^{2}_{1} - A^{2}_{2} }{A^{2}_{1} A^{2}_{2}} \right)$

$V^{2} = \frac{2 g h A^{2}_{1} A^{2}_{2}}{A^{2}_{1} - A^{2}_{2}}$

$V = A_{1} A_{2} \sqrt{\frac{2 g h }{A^{2}_{1} - A^{2}_{2}}}$

Hence flow rate of liquid can be calculated by measuring $h$, since $A_{1}$ and $A_{2}$ are known for the given venturimeter.

Read More

Bernoulli's Theorem and Derivation of Bernoulli's Equation

Statement of Bernoulli's Theorem:

When an ideal fluid (i.e incompressible and non-viscous Liquid or Gas) flows in streamlined motion from one place to another, then the total energy per unit volume (i.e Pressure energy + Kinetic Energy + Potential Energy) at each and every of its path is constant.

$P+\frac{1}{2}\rho v^{2} + \rho gh= constant$

Derivation of Bernoulli's Theorem Equation:

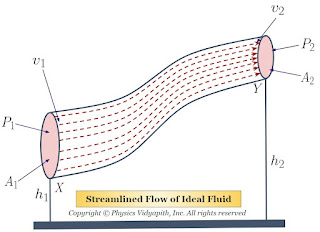
Let us consider that an incompressible and non-viscous liquid is flowing in streamlined motion through a tube $XY$ of the non-uniform cross-section.

Now Consider:

The Area of cross-section $X$ = $A_{1}$
The Area of cross-section $Y$ = $A_{2}$

The velocity per second (i.e. equal to distance) of fluid at cross-section $X$ = $v_{1}$
The velocity per second (i.e. equal to distance) of fluid at cross-section $Y$ = $v_{2}$

The Pressure of fluid at cross-section $X$ = $P_{1}$
The Pressure of fluid at cross-section $Y$ = $P_{2}$

The height of cross-section $X$ from surface = $h_{1}$
The height of cross-section $Y$ from surface = $h_{2}$

The work done per second by force on the liquid Entering the tube at $X$:

$W_{1}$ = Force $ \times $ Distance covered in one second

$W_{1}= P_{1} \times A_{1} \times v_{1} \quad \left( Force =Pressure \times Area \right)$

Similarly
The work done per second by force on the liquid leaving the tube at $Y$:

$W_{2}= P_{2} \times A_{2} \times v_{2}$

The net work done on the liquid:

$\Delta W=W_{1}-W_{2}$
$\Delta W= P_{1} \times A_{1} \times v_{1} - P_{2} \times A_{2} \times v_{2} \qquad(1)$

Now according to the principle of continuity:

$A_{1} v_{1} = A_{2} v_{2} = \frac{m}{\rho} \qquad(2)$

Now from equation $(1)$ and equation $(2)$

$\Delta W=\left( P_{1} -P_{2} \right) \frac {m}{\rho} \qquad(3)$

The kinetic energy of the fluid entering at $X$ in 1 second

$K_{1}=\frac{1}{2}mv_{1}^{2}$

The kinetic energy of the fluid leaving at $Y$ in 1 second

$K_{2}=\frac{1}{2}mv_{2}^{2}$

Therefore, The increase in kinetic energy

$\Delta K = K_{2}-K_{1}$

Now substitute the value of $K_{1}$ and $K_{2}$ in above equation then

$\Delta K = \frac{1}{2}mv_{2}^{2} - \frac{1}{2}mv_{1}^{2}$
$\Delta K = \frac{1}{2}m \left( v_{2}^{2} - v_{1}^{2} \right) \qquad(4)$

The potential energy of fluid at $X$

$U_{1}= mgh_{1}$

The potential energy of fluid at $Y$

$U_{2}= mgh_{2}$

Therefore, The decrease in potential energy

$\Delta U = U_{1}-U_{2}$

Now substitute the value of $U_{1}$ and $U_{2}$ in above equation then

$\Delta U = mgh_{1} - mgh_{2}$
$\Delta U = mg \left( h_{1} - h_{2} \right) \qquad(5)$

This increase in energy is due to the net work done on the fluid, i.e.

Net Work done = Net increase in energy

Net Work done $(\Delta W)$ = Net increase in Kinetic Energy $(\Delta K)$ - Net decrease in Potential Energy $(\Delta U)$

$\left( P_{1} -P_{2} \right) \frac {m}{\rho} = \frac{1}{2}m \left( v_{2}^{2} - v_{1}^{2} \right) - mg \left( h_{1} - h_{2} \right) $

$\left( P_{1} -P_{2} \right) = \frac{1}{2}\rho \left( v_{2}^{2} - v_{1}^{2} \right) -\rho g \left( h_{1} - h_{2} \right) $

$P_{1} + \frac{1}{2} \rho v_{1}^{2} + \rho g h_{1} = P_{2} + \frac{1}{2}\rho v_{2}^{2} + \rho g h_{2} $

$P + \frac{1}{2} \rho v^{2} + \rho g h = Constant $

This is Bernoulli's theorem equation.

Pressure Head, Velocity Head, and Gravitational Head of a Flowing Fluid:

According to Bernoulli's Theorem equation

$P + \frac{1}{2} \rho v^{2} + \rho g h = Constant $

Now dividing the above equation by $\rho g$, then we get

$\frac{P}{\rho g}+\frac{v^{2}}{2g}+ h = Constant$

Where

$\frac{P}{\rho g}$ = Pressure Head

$\frac{v^{2}}{2g}$ = Velocity Head

$h$ = Gravitational Head

The dimension of each of these three is the dimension of height. The sum of these heads is called the 'Total Head'

Therefore, Bernoulli's theorem may also state as follows:

In streamlined motion of an ideal fluid, the sum of pressure head, velocity head and gravitational head at any point is always constant.

When the fluid flows in a horizontal plane $(h_{1}=h_{2})$, then Bernoulli's equation

$P_{1} + \frac{1}{2} \rho v_{1}^{2} = P_{2} + \frac{1}{2}\rho v_{2}^{2} $

$\frac{P}{\rho g}+\frac{v^{2}}{2g} = Constant$

Read More