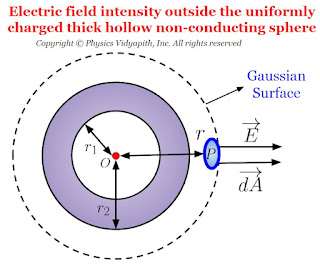
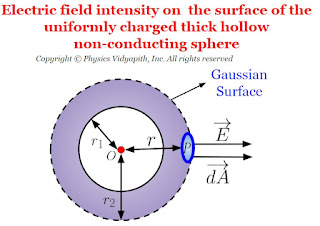
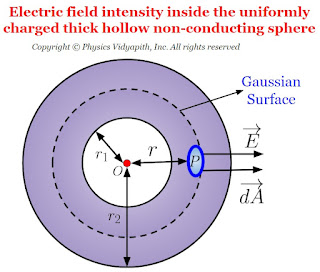
Electric field intensity due to thick hollow non-conducting sphere

Electric field intensity at different points in the field due to uniformly charged thick hollow non-conducting sphere: Let us consider, A hollow non-conducting sphere of inner radius $r_{1}$ and outer radius $r_{2}$ in which $+q$ charge is evenly distributed evenly in the entire volume of the sphere. If $\rho$ is the volume charge density then electric field intensity at different points on the electric field of the thick hollow non-conducting sphere:

1. Electric field intensity outside the thick hollow non-conducting sphere
2. Electric field intensity on the surface of the thick hollow non-conducting sphere
3. Electric field intensity at an internal point of the non-thick hollow conducting sphere

1. Electric field intensity outside the thick hollow non-conducting sphere:

Let us consider, A point $P$ is outside the sphere which is at a $r$ distance from the center point $O$ of the sphere. The direction of electric flux is radially outward in the sphere. So the direction of the electric field vector and the small area vector will be in the same direction i.e. ($\theta =0^{\circ}$). Here $\overrightarrow {dA}$ is a small area element so the small amount of electric flux will pass through this area i.e. →

$ d\phi_{E}= \overrightarrow {E}\cdot \overrightarrow{dA}$

$ d\phi_{E}= E\:dA\: cos\: 0^{\circ} \quad \left \{\because \theta=0^{\circ} \right \}$

$ d\phi_{E}= E\:dA \qquad (1) \quad \left \{\because cos\:0^{\circ}=1 \right \}$

The electric flux passes through the entire Gaussian surface, So integrate the equation $(1)$

$ \oint d\phi_{E}= \oint E\:dA $

$ \phi_{E}=\oint E\:dA\qquad (2)$

According to Gauss's law:

$ \phi_{E}=\frac{q}{\epsilon_{0}}\qquad (3)$

From equation $(2)$ and equation $(3)$, we can write as

$ \frac{q}{\epsilon_{0}}=\oint E\:dA$

$ \frac{q}{\epsilon_{0}}= E\oint dA$

For entire Gaussian spherical surface is

$\oint {dA}=4\pi r^{2}$.

So from the above equations

$ \frac{q}{\epsilon_{0}}= E(4\pi r^{2})$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}} \qquad(4)$

From the above equation, we can conclude that the behavior of the electric field at the external point due to the uniformly charged thick hollow non-conducting sphere is the same as the point charge i.e. like the entire charge is placed at the center.

Since the sphere is a non-conductor so the charge is distributed in the entire volume of the sphere. So charge on the thick hollow sphere-

$q=\frac{4}{3} \pi \left(r_{2}^{3}-r_{1}^{3} \right) \rho $

Substitute this value of charge $q$ in the above equation $(4)$, Therefore,

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{4\pi \left(r_{2}^{3}-r_{1}^{3} \right)\: \rho}{3r^{2}}$

$ E=\frac{\rho}{3 \epsilon_{0}}\frac{\left(r_{2}^{3}-r_{1}^{3} \right)}{r^{2}}$

This equation describes the electric field intensity at the external point of the thick hollow non-conducting sphere.

2. Electric field intensity on the surface of the thick hollow non-conducting sphere:

If point $P$ is placed on the surface of the thick hollow non-conducting sphere i.e. ($r=r_{2}$). so electric field intensity on the surface of the thick hollow non-conducting sphere:

$ E=\frac{\rho}{3\epsilon_{0}}\frac{\left(r^{3}-r_{1}^{3} \right)}{r^{2}}$

3. Electric field intensity at an internal point of the thick hollow non-conducting sphere:

If point $P$ is placed inside the sphere at the distance $r$ from the origin $O$, the electric flux which is passing through the Gaussian surface

$ \phi_{E}= E.4\pi r^{2}$

Where $\phi_{E}=\frac{q'}{\epsilon_{0}}$

$ \frac{q'}{\epsilon_{0}}=E.4\pi r^{2}$

Where $q'$ is part of charge $q$ which is enclosed with Gaussian Surface

$ E=\frac{1}{4 \pi \epsilon_{0}} \frac{q'}{r^{2}} \qquad \qquad (5)$

The charge is distributed uniformly in the entire volume of the sphere so volume charge density $\rho$ will be the same as the entire sphere i.e.

$ \rho=\frac{q}{\frac{4}{3}\pi \left(r_{2}^{3}-r_{1}^{3} \right)}=\frac{q'}{\frac{4}{3}\pi \left(r^{3}-r_{1}^{3} \right)}$

$ \frac{q}{\left(r_{2}^{3}-r_{1}^{3} \right)}=\frac{q'}{\left(r^{3}-r_{1}^{3} \right)}$

$ q'=q\frac{\left(r^{3}-r_{1}^{3} \right) }{\left(r_{2}^{3}-r_{1}^{3} \right)}$

Put the value of $q'$ in equation $(5)$, so

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q} {r^{2}} \frac{\left(r^{3}-r_{1}^{3} \right) }{\left(r_{2}^{3}-r_{1}^{3} \right)}$

Where $q=\frac{4}{3} \pi \left(r_{2}^{3}-r_{1}^{3} \right) \rho $. So above equation can be written as:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{\frac{4}{3} \pi \left(r_{2}^{3}-r_{1}^{3} \right) \rho } {r^{2}} \frac{\left(r^{3}-r_{1}^{3} \right) }{\left(r_{2}^{3}-r_{1}^{3} \right)}$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{\frac{4}{3} \pi \left(r_{2}^{3}-r_{1}^{3} \right) \rho } {r^{2}} \frac{\left(r^{3}-r_{1}^{3} \right) }{\left(r_{2}^{3}-r_{1}^{3} \right)}$

$E=\frac{ \rho }{3 \epsilon_{0}} \frac{\left(r^{3}-r_{1}^{3} \right)}{r^{2}}$

Read More

Electric field intensity due to uniformly charged solid sphere (Conducting and Non-conducting)

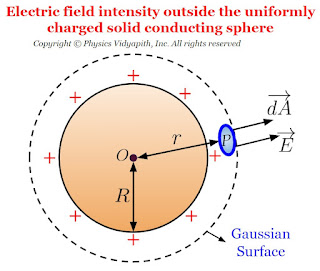
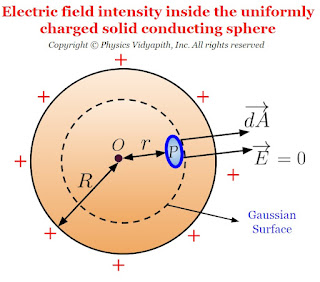
A.) Electric field intensity at different points in the field due to the uniformly charged solid conducting sphere:

Let us consider, A solid conducting sphere that has a radius $R$ and charge $+q$ is distributed on the surface of the sphere in a uniform manner. Now find the electric field intensity at different points due to the solid-charged conducting sphere. These different points are:

1. Electric field intensity outside the solid conducting sphere
2. Electric field intensity on the surface of the solid conducting sphere
3. Electric field intensity inside the solid conducting sphere

1.) Electric field intensity outside the solid conducting sphere:

If $O$ is the center of solid conducting spherical then the electric field intensity outside of the sphere can be determined by the following steps →

1. First, take the point $P$ outside the sphere
2. Draw a spherical surface of radius r which passes through point $P$. This hypothetical surface is known as the Gaussian surface.
3. Now take a small area $\overrightarrow {dA} $ around point $P$ on the Gaussian surface to find the electric flux passing through it.
4. Now find the direction between the electric field vector and a small area vector.

Due to uniform charge distribution, the electric field intensity will be the same at every point on the Gaussian surface. So from the figure,

The direction of electric field intensity on the Gaussian surface is radially outward which is in the direction of the area vector of the Gaussian surface. i.e. ($\theta=0^{\circ}$). Here $\overrightarrow {dA}$ is a small area around point $P$ so the small electric flux $d\phi_{E}$ will pass through this small area $\overrightarrow {dA}$. so this flux can be found by applying Gauss's law in question given below:

$ d\phi_{E}= \overrightarrow {E}\cdot \overrightarrow{dA}$

$ d\phi_{E}= E\:dA\: cos\: 0^{\circ} \quad \left \{\because \theta=0^{\circ} \right \}$

$ d\phi_{E}= E\:dA \quad (1) \quad \left \{\because cos\:0^{\circ}=1 \right \}$

The electric flux passes through the entire Gaussian surface, So integrate the equation $(1)$ →

$ \oint d\phi_{E}= \oint E\:dA $

$\phi_{E}=\oint E\:dA\qquad (2)$

According to Gauss's law:

$ \phi_{E}=\frac{q}{\epsilon_{0}}\qquad (3)$

From equation $(2)$ and equation $(3)$, we can write as

$ \frac{q}{\epsilon_{0}}=\oint E\:dA$

$ \frac{q}{\epsilon_{0}}= E\oint dA$

Now substitute the area of the entire Gaussian spherical is $\oint {dA}=4\pi r^{2}$ in the above equation. So the above equation can be written as:

$ \frac{q}{\epsilon_{0}}= E(4\pi r^{2})$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}}$

From the above equation, we can conclude that the behavior of the electric field at the external point due to the uniformly charged solid conducting sphere is the same as the entire charge is placed at the center, point charge

If the surface charge density is $\sigma$, Then the total charge $q$ on the surface of a solid conducting sphere is→

$ q=4\pi R^{2}\: \sigma$

Substitute this value of charge $q$ in the above equation, so we can write the equation as:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{4\pi R^{2}\: \sigma}{r^{2}}$

$ E=\frac{\sigma}{\epsilon_{0}}\frac{R^{2}}{r^{2}}$

This equation describes the electric field intensity at the external point of the solid conducting sphere.

2.) Electric field intensity on the surface of the solid conducting sphere:

If point $P$ is placed on the surface of the solid conducting sphere i.e. ($r=R$). so electric field intensity on the surface of the solid conducting sphere can be found by putting $r=R$ in the formula of electric field intensity at the external point of the solid conducting sphere:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{R^{2}}$

$ E=\frac{\sigma}{\epsilon_{0}}$

3.) Electric field intensity inside the solid conducting sphere:

If point $P$ is placed inside the solid conducting sphere then electric field intensity will be zero because the charge is distributed uniformly on the surface of the solid sphere and there will not be any charge on the Gaussian surface. So the electric flux will be zero inside the solid sphere. i.e.

$ \phi_{E}=\oint E\:dA$

$ 0=E\oint dA \qquad\quad \left \{ \because \phi_{E}=0 \right \}$

$ E=0$

Electric field intensity distribution with distance for Conducting Solid Sphere:

Electric field intensity distribution with distance shows that the electric field is maximum on the surface of the sphere and zero inside the sphere. Electric field intensity distribution outside the sphere reduces with the distance according to $E=\frac{1}{r^{2}}$.

B.) Electric field intensity at different points in the field due to the uniformly charged solid non-conducting sphere:

Let us consider, A solid non-conducting sphere of radius R in which $+q$ charge is distributed uniformly in the entire volume of the sphere. So electric field intensity at a different point due to the solid charged non-conducting sphere:

1. Electric field intensity outside the solid non-conducting sphere
2. Electric field intensity on the surface of the solid non-conducting sphere
3. Electric field intensity inside the non-solid conducting sphere

1.) Electric field intensity outside the solid non-conducting sphere:

Let us consider, An external point $P$ which is at a distance $r$ from the center point $O$ of the sphere. The electric flux is radially outward in the sphere. So the direction of the electric field vector and the small area vector will be in the same direction i.e. ($\theta =0^{\circ}$). Here $\overrightarrow {dA}$ is a small area, the small amount of electric flux will pass through this area i.e. →

$ d\phi_{E}= \overrightarrow {E}\cdot \overrightarrow{dA}$

$ d\phi_{E}= E\:dA\: cos\: 0^{\circ} \quad \left \{\because \theta=0^{\circ} \right \}$

$ d\phi_{E}= E\:dA \qquad (1) \quad \left \{\because cos\:0^{\circ}=1 \right \}$

The electric flux passes through the entire Gaussian surface, So integrate the equation $(1)$ →

$ \phi_{E}=\oint E\:dA\qquad (2)$

According to Gauss's law:

$ \phi_{E}=\frac{q}{\epsilon_{0}}\qquad (3)$

From equation (1) and equation (2), we can write as

$ \frac{q}{\epsilon_{0}}=\oint E\:dA$

$ \frac{q}{\epsilon_{0}}= E\oint dA$

Now substitute the area of the entire Gaussian spherical surface is $\oint {dA}=4\pi r^{2}$ in the above equation. So the above equation can be written as:

$ \frac{q}{\epsilon_{0}}= E(4\pi r^{2})$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}}$

From the above equation, we can conclude that the behavior of the electric field at the external point due to the uniformly charged solid non-conducting sphere is the same as the point charge i.e. like the entire charge is placed at the center.

Since the sphere is a non-conductor so the charge is distributed in the entire volume of the sphere. So charge distribution can calculate by volume charge density →

$q=\frac{4}{3} \pi R^{3} \rho $

Substitute this value of charge $q$ in the above equation, so we can write the equation as:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{4\pi R^{3}\: \rho}{3r^{2}}$

$ E=\frac{\rho}{\epsilon_{0}}\frac{R^{3}}{3r^{2}}$

This equation describes the electric field intensity at the external point of the solid non-conducting sphere.

2.) Electric field intensity on the surface of the solid non-conducting sphere:

If point $P$ is placed on the surface of a solid non-conducting sphere i.e. ($r=R$). so electric field intensity on the surface of a solid non-conducting sphere can be found by putting $r=R$ in the formula of electric field intensity at the external point of the solid non-conducting sphere:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{R^{2}}$

$ E=\frac{\rho R}{3\epsilon_{0}}$

3.) Electric field intensity inside the solid non-conducting sphere:

If point $P$ is placed inside the sphere and the distance from the origin $O$ is $r$, the electric flux which is passing through the Gaussian surface

$ \phi_{E}= E.4\pi r^{2}$

Where $\phi_{E}=\frac{q'}{\epsilon_{0}}$

$ \frac{q'}{\epsilon_{0}}=E.4\pi r^{2}$

Where $q'$ is part of charge $q$ which is enclosed with Gaussian Surface

$ E=\frac{1}{4 \pi \epsilon_{0}} \frac{q'}{r^{2}} \qquad \qquad (4)$

The charge is distributed uniformly in the entire volume of the sphere so volume charge density $\rho$ will be the same as the entire solid sphere i.e.

$ \rho=\frac{q}{\frac{4}{3}\pi R^{3}}=\frac{q'}{\frac{4}{3}\pi r^{3}}$

$ \frac{q}{\frac{4}{3}\pi R^{3}}=\frac{q'}{\frac{4}{3}\pi r^{3}}$

$ q'=q\frac{r^{3}}{R^{3}}$

$ q'=q\left (\frac{r}{R} \right)^{3}$

Put the value of $q'$ in equation $(4)$, so

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}}\left(\frac{r}{R} \right)^{3}$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{qr}{R^{3}}$

Where $q=\frac{4}{3} \pi R^{3} \rho $. So above equation can be written as:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{\frac{4}{3} \pi R^{3} \rho r}{R^{3}}$

$E=\frac{ \rho r}{3 \epsilon_{0}}$

Electric field intensity distribution with distance for non-conducting Solid Sphere:

Electric field intensity distribution with distance shows that the electric field is maximum on the surface of the sphere and zero at the center of the sphere. Electric field intensity distribution outside the sphere reduces with the distance according to $E=\frac{1}{r^{2}}$.

Read More

The electric potential at different points (like on the axis, equatorial, and at any other point) of the electric dipole

Electric Potential due to an Electric Dipole:

The electric potential due to an electric dipole can be measured at different points:

1. The electric potential on the axis of the electric dipole


2. The electric potential on the equatorial line of the electric dipole


3. The electric potential at any point of the electric dipole

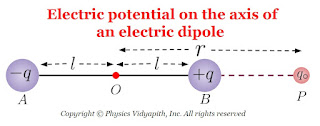
1. The electric potential on the axis of the electric dipole:

Let us consider, An electric dipole AB made up of two charges of -q and +q coulomb is placed in a vacuum or air at a very small distance of $2l$. Let a point $P$ is on the axis of an electric dipole and place at a distance $r$ from the center point $O$ of the electric dipole. Now put the test charged particle $q_{0}$ at point $P$ for the measurement of electric potential due to dipole's charges.

So Electric potential at point $P$ due $+q$ charge of electric dipole→

$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{r-l}$

The electric potential at point $P$ due $-q$ charge of electric dipole→

$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{r+l}$

Electric potential is a scalar quantity. Hence the resultant potential $V$ at the point $P$ will be the algebraic sum of the potential $V_{+q}$ and $V_{-q}$. i.e. →

$ V=V_{+q}+V_{-q}$

Now substitute the value of $V_{+q}$ and $V_{-q}$ in the above equation →

$ V= \frac{1}{4\pi \epsilon_{0}} \frac{q}{r-l} -\frac{1}{4\pi \epsilon_{0}} \frac{q}{r+l}$

$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{q}{r-l} - \frac{q}{r+l} \right]$

$ V= \frac{q}{4\pi \epsilon_{0}} \left[ \frac{1}{r-l} - \frac{1}{r+l} \right]$

$ V= \frac{q}{4\pi \epsilon_{0}} \left[ \frac{ \left( r+l \right)-\left (r-l \right)}{r^{2}-l^{2}} \right]$

$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{2ql}{r^{2}-l^{2}} \right]$

$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{p}{r^{2}-l^{2}} \right] \qquad \left( \because p=2ql\right)$

If $r$ is much larger then $2l$. So $l^{2}$ can be neglected in comparison to $r^{2}$. Therefore electric potential at the point $P$ due to the electric dipole is →

$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{p}{r^{2}} \right] $

2. The electric potential on the equatorial line of the electric dipole:

Let us consider, An electric dipole AB made up of two charges of $+q$ and $-q$ coulomb are placed in vacuum or air at a very small distance of $2l$. Let a point $P$ be on the equatorial line of an electric dipole and place it at a distance $r$ from the center point $O$ of the electric dipole. Now put the test charged particle $q_{0}$ at point $P$ for the measurement of electric potential due to dipole's charges.

So Electric potential at point $P$ due $+q$ charge of electric dipole→

$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{BP}$

$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}}$

The electric potential at point $P$ due $-q$ charge of electric dipole→

$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{AP}$

$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}}$

$\therefore$ The resultant potential at point $P$ is

$ V=V_{+q}+V_{-q}$

$ V=\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}}-\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}} $

$V=0 $

Thus, the electric potential is zero on the equatorial line of a dipole (but the intensity is not zero). So No work is done in moving a charge along this line.

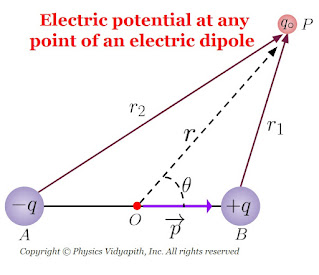
3. The electric potential at any point of the electric dipole:

Let us consider, an electric dipole $AB$ of length $2l$ consisting of the charge $+q$ and $-q$. Let's take a point $P$ in general and its distance is $r$ from the center point $O$ of the electric dipole AB.

Let the distance of point $P$ from the point $A$ and Point $B$ of the dipole is $PB=r_{1}$ and $PA=r_{2}$ respectively.

So, The electric potential at point $P$ due to the $+q$ charge of the electric dipole is →

$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{1}}$

$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{2}}$

The resultant potential at point $P$ is the algebraic sum of potential due to charges $+q$ and $-q$ of the dipole. That is

$ V=V_{+q}+V_{-q}$

$ V=\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{1}}-\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{2}}$

$ V=\frac{1}{4\pi \epsilon_{0}} \left(\frac{q}{r_{1}}-\frac{q}{r_{2}} \right) \qquad(1)$        

Now simplify the above equation by applying the Geometry from the figure. i.e. From the figure, Acute angle $\angle POB$, we can write as,

$ r^{2}_{1}=r^{2}+l^{2}-2rlcos\theta \qquad(2)$

$ r^{2}_{2}=r^{2}+l^{2}-2rlcos \left(\pi - \theta \right)$

$ r^{2}_{2}=r^{2}+l^{2}+2rlcos \theta \qquad(3)$

The equation $(2)$ may be expressed as →

$ r^{2}_{1}=r^{2} \left[1+ \frac{l^{2}}{r^{2}}-\frac{2l}{r}cos\theta \right] $

Taking distance $r$ much greater than the length of dipole (i.e. r>>l), so we may retain only first order term in $\frac{l}{r}$,

$ \therefore r^{2}_{1}=r^{2} \left[1- \frac{2l}{r}cos\theta \right]$

$ r_{1}=r \left[1- \frac{2l}{r}cos\theta \right]^{\frac{1}{2}}$

$ \frac {1}{r_{1}}=\frac{1}{r} \left[1- \frac{2l}{r}cos\theta \right]^{-\frac{1}{2}}$

Now applying the binomial theorem in the above equation. So we get $ \frac {1}{r_{1}}=\frac{1}{r} \left[1+ \frac{l}{r}cos\theta \right]$

Similarly,

$ \frac {1}{r_{2}}=\frac{1}{r} \left[1- \frac{l}{r}cos\theta \right]$

Substituting these values in equation $(1)$, we get

$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{q}{r} \left(1+ \frac{l}{r}cos\theta \right)-\frac{q}{r} \left(1- \frac{l}{r}cos\theta \right) \right]$

$ V=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r} \left[ \left(1+ \frac{l}{r}cos\theta \right)- \left(1- \frac{l}{r}cos\theta \right) \right]$

$ V=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r} \left[ \left(1+ \frac{l}{r}cos\theta \right)- \left(1- \frac{l}{r}cos\theta \right) \right]$

$ V=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r} \left[ \frac{2l cos\theta}{r}\right]$

$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{2ql cos\theta}{r^{2}}\right]$

But $q\times 2l=p$ (dipole moment)

$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{p cos\theta}{r^{2}}\right]$

The vector form of the above equation can be written as →

$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{\overrightarrow{p} \cdot \overrightarrow{r} }{r^{2}}\right]$

The above two equations hold only under the approximation that the distance of observation point $P$ is much greater than the size of the dipole.

Special Case:   

1. At axial points $\theta=0^{\circ}$,
   
   
   then $cos\theta= cos 0^{\circ}=1$,
   
   
   Therefore, $ V=\frac{1}{4\pi\epsilon_{0}} \frac{p}{r^{2}}$
  
2. At equatorial points $\theta=90^{\circ}$,
   
   
   then $cos\theta= cos 90^{\circ}=0$,
   
   
   Therefore,$ \quad V=0$

Now comparing this result with the potential due to a point-charge, we see that:     

1. In a fixed direction, that is , fixed $\theta$, $V\propto \frac{1}{r^{2}}$. here rather than $V \propto \frac{1}{r}$;
  
2. Even for a fixed distance $r$, there is now a dependence on direction, that is, on $\theta$.

Read More

Electric field intensity due to uniformly charged plane sheet and parallel sheet

Electric field intensity due to a uniformly charged infinite plane thin sheet:

Let us consider, A plane charged sheet (It is a thin sheet so it will have surface charge distribution whether it is a conducting or nonconducting sheet) whose surface charge density is $\sigma$. From symmetry, Electric field intensity is perpendicular to the plane everywhere and the field intensity must have the same magnitude on both sides of the sheet. Let point $P_{1}$ and $P_{2}$ be the two-point on the opposite side of the sheet.

To use Gaussian law, we construct a cylindrical Gaussian surface of cross-section area $\overrightarrow{dA}$, which cuts the sheet, with points $P_{1}$ and $P_{2}$. The electric field $\overrightarrow{E}$ is normal to end faces and is away from the plane. Electric field $\overrightarrow{E}$ is parallel to cross-section area $\overrightarrow{dA}$. Therefore the curved cylindrical surface does not contribute to the flux i.e. $\oint \overrightarrow{E} \cdot \overrightarrow{dA}=0$.Hence the total flux is equal to the sum of the contribution from the two end faces. Thus, we get

$ \phi_{E}=\int_{A} \overrightarrow{E} \cdot \overrightarrow{dA}+\int_{A} \overrightarrow{E} \cdot \overrightarrow{dA}$

$ \phi_{E}= \int_{A} E \: dA \:cos 0^{\circ} +\int_{A} E \: dA \:cos 0^{\circ} $

Here the direction of $\overrightarrow{E}$ and $\overrightarrow{dA}$ is same. So the angle will be $\theta = 0^{\circ}$.

Infinite plane thin sheet

$ \phi_{E}= \int_{A} E \: dA +\int_{A} E \: dA $

$ \phi_{E}= \int_{A} 2E \: dA $

$ \phi_{E}= 2E \int_{A} \: dA $

$ \phi_{E}= 2E\:A $

$ \frac{q}{\epsilon_{0}}=2E\:A \qquad \left \{\because \phi_{E}=\frac{q}{\epsilon_{0}} \right \}$

$ E=\frac{q}{2\epsilon_{0} A}$

$\because q=\sigma A $, So the above equation can be written as:

$ E=\frac{\sigma A}{2\epsilon_{0} A} $

$ E=\frac{\sigma}{2\epsilon_{0}} $

Electric field intensity due to the uniformly charged infinite conducting plane thick sheet or Plate:

Let us consider that a large positively charged plane sheet having a finite thickness is placed in the vacuum or air. Since it is a conducting plate so the charge will be distributed uniformly on the surface of the plate. Let $\sigma$ be the surface charge density of the charge

Let's take a point $P$ close to the plate at which electric field intensity has to determine. Since there is no charge inside the conducting plate, this conducting plate can be assumed as equivalent to two plane sheets of charge i.e sheet 1 and sheet 2.

Plane Charged Plate

The magnitude of the electric field intensity $\overrightarrow {E_{1}}$ at point $P$ due to sheet 1 is →

$ E_{1}=\frac{\sigma}{2\epsilon_{0}}$    (away from sheet 1)

The magnitude of the electric field intensity $\overrightarrow {E_{2}}$ at point $P$ due to sheet 2 is →

$ E_{2}=\frac{\sigma}{2\epsilon_{0}}$    (away from sheet 2)

Since $\overrightarrow {E_{1}}$ and $\overrightarrow {E_{2}}$ are in the same direction, the magnitude of resultant intensity $\overrightarrow {E}$ at point $P$ due to both the sheet is →

$ E=E_{1}+E_{2}$

$\because \quad E=\frac{\sigma}{2\epsilon_{0}}+\frac{\sigma}{2\epsilon_{0}}$

$ E=\frac{\sigma}{\epsilon_{0}} $

The resultant electric field will be away from the plate. If the plate is negatively charged, the electric field intensity $\overrightarrow {E}$ would be directed toward the plate.

We have obtained the above formula for a 'plane' charged conductor. In fact, it holds for the electric field intensity 'just' outside a charged conductor of any shape.

Electric field intensity due to two Infinite Parallel Charged Sheets:

When both sheets are positively charged:

Let us consider, Two infinite, plane, sheets of positive charge, 1 and 2 are placed parallel to each other in the vacuum or air. Let $\sigma_{1}$ and $\sigma_{2}$ be the surface charge densities of charge on sheet 1 and 2 respectively.

Likely positive charged sheet

Let $\overrightarrow {E_{1}}$ and $\overrightarrow {E_{2}}$ be the electric field intensities at any point due to sheet 1 and sheet 2 respectively. Then,

The electric field intensity at points $P'$ →

$ E_{1}=\frac{\sigma_{1}}{2\epsilon_{0}}$    (away from sheet 1)

$ E_{2}=\frac{\sigma_{2}}{2\epsilon_{0}}$    (away from sheet 2)

Since, Electric field intensities $\overrightarrow {E_{1}}$ and $\overrightarrow {E_{2}}$ are in the same direction, the magnitude of resultant intensity at point $P'$ is given by →

$ E=E_{1}+E_{2}$

$ E=\frac{\sigma_{1}}{2 \epsilon_{0}}+\frac{\sigma_{2}}{2 \epsilon_{0}}$

$ E=\frac{1}{2 \epsilon_{0}} \left (\sigma_{1}+\sigma_{2} \right )$

If both sheets have equal charge densities $\sigma$ i.e. $\sigma_{1}=\sigma_{2}=\sigma$, Then above equation can be written as:

$ E=\frac{\sigma}{ \epsilon_{0}} $

This electric field intensity would be away from both sheet 1 and sheet 2.

The electric field intensity at points $P$→

Electric field intensity at point $P$ due to sheet 1 is →

$ E_{1}=\frac{\sigma_{1}}{2\epsilon_{0}}$    (away from sheet 1)

$ E_{2}=\frac{\sigma_{2}}{2\epsilon_{0}}$    (away from sheet 2)

Now, both electric field intensities $\overrightarrow{E_{1}}$ and $\overrightarrow{E_{2}}$ are in opposite direction. The magnitude of resultant electric field $\overrightarrow{E}$ at point $P$ is given by

$ E= E_{1}-E_{2}$

$ E=\frac{\sigma_{1}}{2 \epsilon_{0}}-\frac{\sigma_{2}}{2 \epsilon_{0}}$

$ E=\frac{1}{2 \epsilon_{0}} \left (\sigma_{1}-\sigma_{2} \right )$

If both sheets have equal charge densities $\sigma$ i.e. $\sigma_{1}=\sigma_{2}=\sigma$, Then above equation can be written as:

$ E=0 $

The electric field intensity at points $P''$ → $ E_{1}=\frac{\sigma_{1}}{2\epsilon_{0}}$    (away from sheet 1)

$ E_{2}=\frac{\sigma_{2}}{2\epsilon_{0}}$    (away sheet 2)

Since, Electric field intensities $\overrightarrow {E_{1}}$ and $\overrightarrow {E_{2}}$ are in the same direction, the magnitude of resultant intensity at point $P''$ is given by →

$ E=E_{1}+E_{2}$

$ E=\frac{\sigma_{1}}{2 \epsilon_{0}}+\frac{\sigma_{2}}{2 \epsilon_{0}}$

$ E=\frac{1}{2 \epsilon_{0}} \left (\sigma_{1}+\sigma_{2} \right )$

If both sheets have equal charge densities $\sigma$ i.e. $\sigma_{1}=\sigma_{2}=\sigma$, Then above equation can be written as:

$ E=\frac{\sigma}{ \epsilon_{0}} $

This electric field intensity would be away from both sheet 1 and sheet 2.

When one-sheet is positively charged and the other sheet negatively charged:

Let us consider two sheets 1 and 2 of positive and negative charge densities $\sigma_{1}$ and $\sigma_{2}$ ($\sigma_{1} > \sigma_{2}$)

Unlike charged parallel Sheet

The electric field intensities at point $P'$ →

$ E_{1}=\frac{\sigma_{1}}{2\epsilon_{0}}$    (away from sheet 1)

$ E_{2}=\frac{\sigma_{2}}{2\epsilon_{0}}$    (toward from sheet 2)

The magnitude of the resultant electric field $E$

$ E=E_{1}-E_{2}$

$E= \frac{1}{2\epsilon_{0}} \left ( \sigma_{1}- \sigma_{2}\right )$

If both sheets have equal charge densities $\sigma$ i.e. $\sigma_{1}=\sigma_{2}=\sigma$, Then above equation can be written as:

$ E=0 $

The electric field intensities at point $P$ →

$ E_{1}=\frac{\sigma_{1}}{2\epsilon_{0}}$    (away from sheet 1)

$ E_{2}=\frac{\sigma_{2}}{2\epsilon_{0}}$    (towards sheet 2)

Since, Electric field intensities $\overrightarrow {E_{1}}$ and $\overrightarrow {E_{2}}$ are in the same direction, the magnitude of resultant intensity at point $P$ is given by →

$ E=E_{1}+E_{2}$

$ E=\frac{\sigma_{1}}{2 \epsilon_{0}}+\frac{\sigma_{2}}{2 \epsilon_{0}}$

$ E=\frac{1}{2 \epsilon_{0}} \left (\sigma_{1}+\sigma_{2} \right )$

If both sheets have equal charge densities $\sigma$ i.e. $\sigma_{1}=\sigma_{2}=\sigma$, Then above equation can be written as:

$ E=\frac{\sigma}{ \epsilon_{0}} $

The electric field intensities at point $P''$ →

$ E_{1}=\frac{\sigma_{1}}{2\epsilon_{0}}$    (away from sheet 1)

$ E_{2}=\frac{\sigma_{2}}{2\epsilon_{0}}$    (toward from sheet 2)

The magnitude of the resultant electric field $E$ →

$ E=E_{1}-E_{2}$

$E= \frac{1}{2\epsilon_{0}} \left ( \sigma_{1}- \sigma_{2}\right )$

If both sheets have equal charge densities $\sigma$ i.e. $\sigma_{1}=\sigma_{2}=\sigma$, Then above equation can be written as:

$ E=0 $

From the above expression, we can conclude that the magnitude of $E$ is free from the 'position' of the point taken in the electric field between the sheet and outside the sheet. It is also shown that the electric field between the sheet is uniform everywhere and independent of separation between the sheets.

Read More

Electric field intensity due to uniformly charged wire of infinite length

Derivation of electric field intensity due to the uniformly charged wire of infinite length: Let us consider a uniformly-charged (positively charged) wire of infinite length having a constant linear charge density (that is, a charge per unit length) $\lambda$ coulomb/meter. Let P is a point at a distance $r$ from the wire at which electric field $\overrightarrow{E}$ has to find.

Let us draw a coaxial Gaussian cylindrical surface of length $l$ through point $P$. By symmetry, the magnitude $E$ of the electric field will be the same at all points on this surface and directed radially outward. Thus, Now take small area elements $dA_{1}$, $dA_{2}$ and $dA_{3}$ on the Gaussian surface as shown in figure below. Therefore, the total electric flux passing through area elements is:

$ \phi_{E}= \oint \overrightarrow{E} \cdot \overrightarrow{dA_{1}} + \oint \overrightarrow{E} \cdot \overrightarrow{dA_{2}} + \oint\overrightarrow{E} \cdot \overrightarrow{dA_{3}}$

$ \phi_{E}= \oint E\: dA_{1} cos\theta_{1} + \oint E\: dA_{2} cos\theta_{2} + \oint E\: dA_{3} cos\theta_{3}$

The angle between the area element $dA_{1}$, $dA_{2}$ and $dA_{3}$ with electric field are $\theta_{1}= 0^{\circ}$ , $\theta_{2}= 90^{\circ}$, and $\theta_{3}=90^{\circ}$ respectively. So electric flux

$ \phi_{E}= \oint E\: dA_{1} cos0^{\circ} + \oint E\: dA_{2} cos90^{\circ} + \oint E\: dA_{3} cos90^{\circ}$

Here $cos \: 0^{\circ}=1$ and $cos \: 90^{\circ}=0$

Hence the above equation can be written as: $ \phi_{E}= \oint E\:dA_{1} $

The total electric flux passing through the Gaussian surface is

$ \phi_{E}= \oint{E\:dA_{1}} $

$ \phi_{E}= E\:\oint{dA_{1}} $

$ \phi_{E}= E\:\left(2\pi r l \right) \qquad \left\{\because \oint{dA_{1}} =2\pi r l \right\} $

$ \phi_{E}= E\:\left(2\pi r l \right)$

But, By Gaussian's law, The total flux $\phi_{E}$ must be equal to $\frac{q}{\epsilon_{0}}$, where $q$ is the total charge enclosed with the Gaussian surface. so that

$ \frac{q}{\epsilon_{0}}= E\:\left(2\pi r l \right)$

$ E= \frac{q}{2\pi r l \epsilon_{0}}$

For linear charge distribution → $q=\lambda l$. So substitute this value in the above equation which can be written as

$ E= \frac{\lambda l}{2\pi r l \epsilon_{0}}$

$ E= \frac{\lambda}{2\pi\epsilon_{0} r }$

The vector form of the above equation :

$\overrightarrow{E}= \frac{\lambda}{2\pi\epsilon_{0} r }\widehat{r}$

Where $\widehat{r}$ is a unit vector in the direction of $r$. The direction of $\overrightarrow{E}$ is radially outwards(for positively charged wire).

Thus, the electric field ($E$) due to the linear charge is inversely proportional to the distance ($r$) from the linear charge and its direction is outward perpendicular to the linear charge.

Special Note: A charged cylindrical conductor behaves for external points as the whole charge is distributed along its axis.

Read More

Electric field intensity due to point charge by Gauss's Law

Derivation of electric field intensity due to a point charge by Gauss's Law: Let us consider, a source point charge particle of $+q$ coulomb is placed at point $O$ in space. Let's take a point $P$ on the electric field of the source point charge particle. To find the electric field intensity $\overrightarrow{E}$ at point $P$, first put the test charge particle $+q_{0}$ on the point $P$ and draw a gaussian surface which passes through the point $P$. After that take a very small area $\overrightarrow{dA}$ around the point $P$. If the distance between the source charge particle and small area $\overrightarrow {dA}$ is $r$ then electric flux passing through the small area $\overrightarrow{dA}$ →

$ d\phi_{E}= \overrightarrow{E} \cdot \overrightarrow{dA}$

$ d\phi_{E}= E\:dA\: cos\theta$

Electric field due to point charge

from the figure, the direction between $\overrightarrow{E}$ and $\overrightarrow{dA}$ is parallel to each other i.e. the angle will be $0^{\circ}$. So the above equation can be written as →

$ d\phi_{E}= E\:dA\: cos0^{\circ}$

$ d\phi_{E}= E\:dA $

The electric flux passing through the entire Gaussian surface and be found by closed integration of the above equation →

$ d\phi_{E}= \oint {E\:dA} $

$ d\phi_{E}= E\:\oint {dA} $

$ \phi_{E}= E\left(4\pi r^{2} \right) \qquad \left\{ \because \oint {dA}=4\pi r^{2} \right\}$

According to Gauss's Law → $\phi_{E}= \frac{q}{\epsilon_{0}}$ then above equation can be written as →

$ \frac{q}{\epsilon_{0}}= E \left(4\pi r^{2} \right)$

$ E= \frac{1}{4\pi\epsilon_{0}} \frac{q}{r^{2}}$

The above expression is the electric field intensity due to a point source charged particle.

Read More

The electric potential energy of an electric dipole in the uniform electric field

Derivation of the electric potential energy of an electric dipole in the uniform electric field:

Let us consider an electric dipole $AB$, which is made up of two charges $q_1$ and $q_2$, which are placed at a distance of $2l$ in the electric field $E$. So force acting on each charge due to the electric field will be $qE$. If the dipole gets rotated a small-angle $d\theta$ against the torque acting on it in the uniform electric field $E$ then the small work done is

$dW=\tau. d\theta \qquad (1)$

Force of moment on an electric Dipole

The torque (i.e moment of force) on an electric dipole in a uniform electric field

$ \tau=p.E\:sin\theta$

Now substitute the value of $\tau$ in equation $(1)$. So work done

$ dW=p.E\:sin\theta.d\theta$

If the dipole rotate the angle from $\theta_{1}$ to angle $\theta_{2}$ then workdone

$\int_{W_{1}}^{W_{2}}dW=p.E\int_{\theta_{1}}^{\theta_{2}}sin\theta \: d\theta$

$ W_{2}-W_{1}=p.E\left[-cos\theta \right]_{\theta_{1}}^{\theta_{2}}$

$ \Delta W= p.E \left( cos\theta_{1}-cos\theta_{2} \right)\qquad\qquad (2)$

This work is stored in the form of the electric potential energy of an electric dipole in the electric field. So

$U=\Delta W$

$U=p.E \left( cos\theta_{1}-cos\theta_{2} \right)$

If the electric dipole rotates from $0^{\circ}$ (when the direction of electric dipole moment $p$ is aligned in the direction of the electric field $E$) to an angle $\theta$ in the electric field i.e $\theta_{1}=0^{\circ}$ and $\theta_{2}=\theta$ then the electric potential energy of dipole in a uniform electric field

$U=p.E (1-cos\theta)$

Case-(I) If $\theta=0^{\circ}$ i.e It is stable equilibrium position then

$U_{min}=-pE$

Case-(II) If $\theta=90^{\circ}$ i.e Position of zero energy then

$U=0$

Case-(III) If $\theta=180^{\circ}$ i.e It is unstable equilibrium position then

$U_{max}=pE$

Read More

Force between multiple charges (Superposition principle of electrostatic forces)

Principle of Superposition for Electric force:

If a system contains a number of interacting charges, then the net force on anyone charge equals the vector sum of all the forces exerted on it by all the other charges. This is the principle of Superposition for electric force.

If a system contains n point charges $ q_{1},q_{2},q_{3}........q_{n}$. Then according to the principle of superposition, the force acting on the charge due to all the other charges

$\overrightarrow{F_{1}}=\overrightarrow{F_{12}}+\overrightarrow{F_{13}}+\overrightarrow{F_{14}}+...+\overrightarrow{F_{1n}} \qquad (1)$

Where $\overrightarrow{F_{12}}$ is the force on charge $q_{1}$ due to charge $q_{2}$, $\overrightarrow{F_{13}}$ that is due to $q_{3}$ and $\overrightarrow{F_{1n}}$ that due to $q_{n}$.

If the distance between the charges $q_{1}$ and $q_{2}$ is $\widehat{r}_{12}$ (magnitude only) and $\widehat{r}_{21}$ is unit vector from charge $q_{2}$ to $q_{1}$, then

$\overrightarrow{F_{12}}=\frac{1}{4\pi \epsilon _{0}}\frac{q_{1}q_{2}}{r_{12}^{2}}\:\hat{r_{21}} \qquad (2)$

Similarly, the forces on charge $q_{1}$ due to other charges are given by

$ \overrightarrow{F_{13}}=\frac{1}{4\pi \epsilon _{0}}\:\frac{q_{1}q_{3}}{r_{13}^{2}}\:\hat{r_{31}}\qquad (3)$

$.............................$

$.............................$

$ \overrightarrow{F_{1n}}=\frac{1}{4\pi \epsilon _{0}}\:\frac{q_{1}q_{n}}{r_{1n}^{2}}\:\hat{r_{n1}}\qquad (n)$

Hence, putting the value of $\overrightarrow{F_{12}},\overrightarrow{F_{13}},\overrightarrow{F_{14}}......\overrightarrow{F_{1n}}$, in equation $(1)$, the total force on charge $q_{1}$ due to all other charges is given by

$ \overrightarrow{F_{1}}=\frac{1}{4\pi \epsilon _{0}}[\:\frac{q_{1}q_{2}}{r_{12}^{2}}\:\hat{r_{21}}+\frac{q_{1}q_{3}}{r_{13}^{2}}\:\hat{r_{31}}+....\\ \quad\quad\quad ..+\frac{q_{1}q_{n}}{r_{1n}^{2}}\:\hat{r_{n1}}]$

The same procedure can be applied to finding the force on any other charge due to all the remaining charges. For example, the force on $q_{2}$ due to all the other charges is given by

$ \overrightarrow{F_{2}}=\frac{1}{4\pi \epsilon _{0}}[\:\frac{q_{2}q_{1}}{r_{21}^{2}}\:\hat{r_{12}}+\frac{q_{2}q_{3}}{r_{23}^{2}}\:\hat{r_{32}}+... \\ \quad\quad\quad ..+\frac{q_{2}q_{n}}{r_{2n}^{2}}\:\hat{r_{n2}}\:]$

Some Observations Points of Coulomb's Law:

There are the following point has been observed in Coulomb's law, that are

1. Coulomb's force between the two charges is directly proportional to the product of the magnitude of the charge.
   
   
   $ F\propto q_{1}q_{2}$


2. Coulomb's force between the two charges is inversely proportional to the square of the distance between the two charges.
   
   
   $F\propto \frac{1}{r^{2}}$


3. The electrostatic force acts between the line joining the charges. In two charges, one charge is assumed to be at rest for the calculation of the force on the second charge. So It is also known as a central force.


4. The magnitude of the electrostatic force is equal and the direction of force is opposite. So the electrostatic force is also known as the action and reaction pair.


5. The electrostatic force between two charge does not affect by the presence and absence of any other charges but the net force increase on the source charge.

Read More

Derivation of torque on an electric dipole in an uniform and a non-uniform electric field

Torque on an electric dipole in a uniform electric field: Let us consider, An electric dipole AB, made up of two charges $+q$ and $-q$, is placed at a very small distance $2l$ in a uniform electric field $\overrightarrow{E}$. If $\theta$ is the angle between electric field intensity $\overrightarrow{E}$ and electric dipole moment $\overrightarrow{p}$ then the magnitude of electric dipole moment →

$\overrightarrow{p}=q\times\overrightarrow{2l}\qquad(1)$

Force exerted on charge $+q$ by electric field $\overrightarrow{E}$ →

$\overrightarrow{F_{+q}}=q\overrightarrow{E}\qquad(2)$

Here in the above equation(2), the direction of $\overrightarrow{F}$ is along the direction of $\overrightarrow{E}$

Force exerted on charge $-q$ by electric field $\overrightarrow{E}$ →

$\overrightarrow{F_{-q}}=-q\overrightarrow{E}\qquad(3)$

Here in the above equation(3) the direction of $\overrightarrow{F}$ is in the opposite direction of $\overrightarrow{E}$

So, the net force of on an electric dipole→

$\overrightarrow{F}=\overrightarrow{F_{+q}}+\overrightarrow{F_{-q}}\qquad (4)$

Now substitute the value of equation $(2)$ and equation $(3)$ in above equation $(4)$. so net force→

$\overrightarrow{F}=0\qquad (5)$

Torque on electric dipole

Hence, the net translating force on an electric dipole in a uniform electric field is zero. But these two force is equal in magnitude, opposite in direction, and act at different point of the dipole so these force form a coupling force that exerts a torque on an electric dipole→

Torque = force x Perpendicular distance between the two forces

$\overrightarrow{\tau}=(qE).2l\:sin\theta\quad\quad\quad\quad(6)$

$ \overrightarrow{\tau}=pE\:sin\theta$

$\overrightarrow{\tau}=\overrightarrow{p}\times\overrightarrow{E}$

Case(I)→ If the dipole is placed perpendicular to the electric field i.e. $\theta=90^{\circ}$, the torque acting on it will be maximum. i.e.

$ \tau_{max}=pE $

Case(II)→ If the dipole is placed parallel to the electric field i.e. $\theta=0^{\circ}$ or $\theta=180^{\circ}$, the torque acting on it will be minimum. i.e.

$ \tau_{min}=0$

Direction of torque

Electric Dipole Moment:

We know that the torque

$ \overrightarrow{\tau}=pE\:sin\theta$

If $E=1$ and $\theta=90^{\circ}$ Then

$ \tau_{max} =p$

Hence Electric dipole moment is the torque acting on the dipole placed perpendicular to the direction of uniform electric field intensity.

Torque on an electric dipole in a non-uniform electric field:

In a non-uniform electric field, the $+q$ and $-q$ charges of a dipole experience different forces (not equal in magnitude and opposite in direction) at a slightly different position in the electric field, and hence a net force $\overrightarrow{F}$ act on the dipole in a non-uniform field. A net torque acts on the dipole which depends on the location of the dipole in the non-uniform field.

$\overrightarrow{\tau}=\overrightarrow{p}\times\overrightarrow{E}(\overrightarrow{r})$

Where $\overrightarrow{r}$ is the position vector of the center of the dipole.

When p and E are Parallel

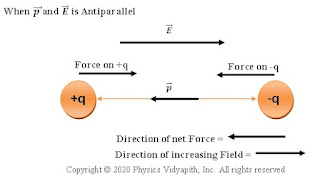
In the non-uniform field, If the direction of the dipole moment $\overrightarrow{p}$ is parallel to electric field intensity $\overrightarrow{E}$ or antiparallel to electric field intensity $\overrightarrow{E}$ the net torque on the dipole is zero because the force on charges becomes linear.

When p and E are antiparallel

However, If $\overrightarrow{p}$ is parallel to $\overrightarrow{E}$, a net force on the dipole in the direction of increasing $\overrightarrow{E}$. When $\overrightarrow{p}$ is antiparallel to $\overrightarrow{E}$, a net force on the dipole in the direction of decreasing $\overrightarrow{E}$. As shown in the figure above.

Read More

Electric Dipole and Derivation of Electric field intensity at different points of an electric dipole

Electric Dipole:

An electric dipole is a system in which two equal magnitude and opposite point charged particles are placed at a very short distance apart.

Electric Dipole Moment:

The product of magnitude of one point charged particle and the distance between the charges is called the 'electric dipole moment'. It is vector quantity and the direction of electric dipole moment is along the axis of the dipole pointing from negative charge to positive charge.

Electric Dipole

Let us consider, the two charged particle, which has equal magnitude $+q$ coulomb and $-q$ coulomb is placed at a distance of $2l$ in a dipole so the electric dipole moment is →

$\overrightarrow{p}=q\times \overrightarrow{2l}$

Unit: $C-m$ Or $Ampere-metre-sec$

Dimension: $[ALT]$

Electric field intensity due to an Electric Dipole:

The electric field intensity due to an electric dipole can be measured at three different points:

1. Electric field intensity at any point on the axis of an electric dipole


2. Electric field intensity at any point on the equatorial line of an electric dipole


3. Electric field intensity at any point on an electric dipole

1. Electric field intensity at any point on the axis of an electric dipole:

Let us consider, An electric dipole $AB$ made up of two charges of $-q$ and $+q$ coulomb are placed in a vacuum or air at a very small distance of $2l$. Let a point $P$ be on the axis of an electric dipole and place it at a distance $r$ from the center point $O$ of the electric dipole. Now put the test charged particle $q_{0}$ at point $P$ for the measurement of electric field intensity due to dipole's charge.

Electric field intensity at any point on the axis of an electric dipole

So, Electric field intensity (magnitude only) at point $P$ due $+q$ charge of electric dipole

$ E_{+q}=\frac{1}{4\pi\epsilon}\frac{q}{(r-l)^{2}} \qquad(1)$

Electric field intensity (magnitude only) at point $P$ due $-q$ charge of electric dipole

$ E_{-q}=\frac{1}{4\pi\epsilon_{0}}\frac{q}{(r+l)^{2}} \qquad(2)$

The net electric field at point $P$ due to an electric dipole

$ E=E_{+q}-E_{-q}\qquad(3)$

Subtitute the value of $E_{+q}$ and $E_{-q}$ in equation $(3)$, Then the above equation $(3)$ can also be written as follows

$E=\frac{q}{4\pi\epsilon _{0}}\left [ \frac{1}{(r-l)^{2}}-\frac{1}{(r+l)^{2}} \right ]$

$ E=\frac{q}{4\pi\epsilon _{0}}\left [ \frac{(r+l)^{2}-(r-l)^{2}}{(r+l)^{2}(r-l)^{2}} \right ]$

$ E=\frac{q}{4\pi\epsilon _{0}}\left [ \frac{(r^{2}+l^{2}+2lr-r^{2}-l^{2}+2lr)}{(r+l)^{2}(r-l)^{2}} \right ]$

$ E=\frac{q}{4\pi\epsilon _{0}}\left [ \frac{4rl}{(r^{2}-l^{2})^{2}} \right ]\qquad(4)$

Here $l \lt r $ so $l^{2} \lt \lt r^{2}$ therefore neglect the term $l^{2}$ in above equation $(4)$ so we can write above equation

$ E=\frac{q}{4\pi\epsilon _{0}}\left [ \frac{4rl}{(r^{2})^{2}} \right ]$

$E=\frac{1}{4\pi\epsilon _{0}}\left [ \frac{2p}{r^{3}} \right ]\qquad (5)$

This is the equation of electric field intensity at a point on the axis of an electric dipole.

The vector form of the above equation $(5)$ is

$\overrightarrow{E}=\frac{1}{4\pi\epsilon _{0}}\left [ \frac{2\overrightarrow{p}}{r^{3}} \right ]$

2. Electric field intensity at any point on the equatorial line of an electric dipole:

Let us consider, An electric dipole $AB$ made up of two charges of $+q$ and $-q$ coulomb are placed in vacuum or air at a very small distance $2l$. Let a point $P$ be on the equatorial line of an electric dipole and place it at a distance $r$ from the center point $O$ of the electric dipole. Now put the test charged particle $q_{0}$ at point $P$ for the measurement of electric field intensity due to dipole's charge.

So, Electric field intensity (magnitude only) at point $P$ due $+q$ charge of electric dipole

Electric field intensity at a point of the equatorial line of an electric dipole

$E_{+q}=\frac{1}{4\pi\epsilon_{0}}\left [\frac{q}{(r^{2}+l^{2})} \right ] \qquad(1)$

Electric field intensity (magnitude only) at point $P$ due to $-q$ charge of electric dipole

$E_{-q}=\frac{1}{4\pi\epsilon_{0}}\left [\frac{q}{(r^{2}+l^{2})} \right ] \qquad(2)$

The net electric field at point $P$ due to an electric dipole

$E=E_{+q}\:cos\theta + E_{-q}\: cos\theta \qquad(3)$

Put the value of $E_{+q}$ and $E_{-q}$ in the above equation $(3)$, So equation $(3)$ can also be written as follows

$E=2\left [ \frac{q}{4\pi\epsilon_{0} }\frac{1}{(r^{2}+l^{2})} \right ]cos\theta \qquad (4)$

From figure, In $\Delta \: POB$,

$cos\:\theta=\frac{l}{\sqrt{(r^{2}+l^{2})}}$

Put the value of $cos\theta$ in equation $(4)$, so equation $(4)$ can also be written as follows

$E=\frac{1}{4\pi\epsilon_{0}}\left [ \frac{q\times2l}{(r^{2}+l^{2})^{3/2}} \right ] \qquad (5)$

Here $l \lt r$ so $l^{2} \lt \lt r^{2}$ so neglect the term $l^{2}$ in above equation $(5)$ so we can write above equation

$ E=\frac{1}{4\pi\epsilon_{0}}\left [ \frac{q\times2l}{r^{3}} \right ] \qquad (6)$

$E=\frac{1}{4\pi\epsilon_{0}} \frac{p}{r^{3}} \qquad (7)$

This is the equation of electric field intensity at a point on the equatorial line of an electric dipole.

The vector form of the above equation $(7)$ is

$\overrightarrow{E}=\frac{1}{4\pi\epsilon_{0}} \frac{\overrightarrow{p}}{r^{3}}$

3. Electric field intensity at any point of an electric dipole:

Let us consider, An electric dipole $AB$ of length $2l$ consisting of the charge $+q$ and $-q$. Let's take a point $P$ in general and its position vector is $\overrightarrow{r}$ from the center point $O$ of the electric dipole AB.

Electric field intensity at any point of an electric dipole

The electric dipole moment is a vector quantity that has a direction from $-q$ charge to $+q$ charge. So the electric dipole moment's direction is resolved in two-component one is along the vector position $\overrightarrow{r}$ i.e pcosθ and the other is normal to vector position $\overrightarrow{r}$ i.e $psinθ$. So

Electric field intensity due to dipole moment of component $p\:cos\theta$ {Electric field along the Axial Line }

$ \overrightarrow{E_{\parallel }}=\frac{1}{4\pi\epsilon_{0}} \frac{2pcos\theta}{r^{3}} \qquad(1)$

Electric field intensity due to dipole moment of component $p\:sin\theta$ {Electric field along the Equatorial Line}

$ \overrightarrow{E_{\perp}}=\frac{1}{4\pi\epsilon_{0}} \frac{psin\theta}{r^{3}} \qquad(2)$

The resultant electric field vector $E$ at point $P$

$ \overrightarrow{E}=\sqrt{E_{\perp}^{2}+E_{\parallel}^{2}+2 E_{\perp}E_{\parallel}cos90^{\circ}}$

From figure, The angle between $E_{\perp}$ and $E_{\parallel}$ is $90^{\circ}$. So

$\overrightarrow{E}=\sqrt{E_{\perp}^{2}+E_{\parallel}^{2} }\qquad (3)$

Now substitute the value of equation $(1)$ and equation $(2)$ in equation $(3)$. Then

$ \overrightarrow{E}=\frac{1}{4\pi\epsilon_{0}}\frac{p}{r^{3}}\sqrt{(sin^{2}\theta+4cos^{2}\theta)}$

$ \overrightarrow{E}=\frac{1}{4\pi\epsilon_{0}}\frac{p}{r^{3}}\sqrt{(1+3cos^{2}\theta)}$

This is the equation of electric field intensity at any point due to an electric dipole.

The direction of the resultant electric field intensity vector $\overrightarrow{E}$ from the axial line is

$tan\alpha =\frac{\overrightarrow{E}_{\perp }}{\overrightarrow{E_{\parallel }}} \qquad(4)$

Put the value of $\overrightarrow{E_{\perp}}$ and $\overrightarrow{E_{\parallel}}$ in equation (4). we get

$tan\alpha =\frac{sin\theta}{2cos\theta}$

$tan\alpha =\frac{1}{2}tan\theta$

Here $\alpha$ is the angle between the resultant electric field intensity $\overrightarrow{E}$ and the axial line.

Read More

Electric field Intensity (Definition) and Electric field Intensity due to point charge

Definition of Electric Field Intensity:

The force acting on the per unit test charge in electric field is called the Electric field intensity. It is represented by $'E'$.

Let us consider that a test-charged particle of $q_{0}$ Coulomb is placed at a point in the electric field and a force $F$ acting on them so the electric field intensity at that point

$ \overrightarrow{E}=\frac{\overrightarrow{F}}{q_{0}}$

SI Unit:$\quad Newton/Coulomb$ $ (N/C)$ $\quad Kg-m^{2}/sec^{3} A$

Dimension: $\left [ML^{2}T^{-3}A^{-1} \right ]$

Physical Significance of Electric Field:

The force experienced by a charge is different at different points in space. So electric field intensity also varies from point to point. In general, Electric field intensity is not a single vector quantity but it is a set of infinite vector and each point in space have a unique electric field intensity. So electric field is an example of the vector field.

Electric Field Intensity due to a Point Charge:

Let us consider that an isolated point charge of $+q$ Coulomb is placed at a point $O$ in a medium whose dielectric constant is $K$. If a test charge particle of $q_{0}$ Coulomb is placed at a point $P$ in the electric field at a distance $r$ from point $O$. So the electric field intensity (magnitude form) at point $P$

Electric field intensity due to a point charge

$E=\frac{F}{q_{0}}\qquad (1)$

According to Coulomb's Law:

$F=\frac{1}{4\pi \varepsilon _{0}K}\frac{qq_{0}}{r^{2}}\qquad (2)$

From equation $(1)$ and equation $(2)$, we can write

$E=\frac{1}{4\pi \varepsilon _{0}K}\frac{q}{r^{2}} \qquad (3)$

For air or vacuum $K=1$, Then from equation $(3)$

$E=\frac{1}{4\pi \varepsilon _{0}}\frac{q}{r^{2}} \qquad (4)$

Where

$\frac{1}{4\pi \varepsilon _{0}}=9\times10^{9} N-m^{2}/C^{2}$

From equation $(4)$

$E=9\times 10^{9} \frac{q}{r^{2}}\qquad (5)$

In Vector Notation:

$\overrightarrow{E}=\frac{1}{4\pi \varepsilon _{0}K}\frac{q}{r^{2}}r\hat{}$

If a system containing $'n'$ point charge $q_{1},q_{2},q_{3},..........q_{n}$ then electric field intensity due to the system of charge particle will be equal to the vector sum of the intensities i.e.

$\overrightarrow{E}=\overrightarrow{E_{1}}+\overrightarrow{E_{2}}+\overrightarrow{E_{3}}+....+\overrightarrow{E_{n}}$

$\overrightarrow{E}=\frac{1}{4\pi \varepsilon _{0}K}\sum_{i=0}^{n}\frac{q_{i}}{r_{i}^{2}}r_{i}\hat{}$

Where $r_{i}$ is the distance from point $'P'$ to charge $q_{i}$.

Read More

Work done by a rotating electric dipole in uniform electric field

Derivation:

Let us consider, An electric dipole AB, made up of two charges $+q$ and $-q$, is placed at a very small distance $2l$ in a uniform electric field $\overrightarrow{E}$. If dipole $AB$ rotates at angle $θ$ from its equilibrium position. If $A'$ and $B'$ are the new position of a dipole in the electric field. Then force on $+q$ charge particle due to electric field→

$ \overrightarrow{F_{+q}}=q\overrightarrow{E}\qquad (1)$

Then force on $-q$ charge particle due to electric field→

$ \overrightarrow{F_{-q}}=q\overrightarrow{E}\qquad(2)$

Work done by rotating an electric dipole 

So work done by a force on $+q$ charge particle to bring from position $A$ to position $A'$→

$ \overrightarrow{W_{+q}}=\overrightarrow{F_{+q}}·\overrightarrow{AC}$

$ \overrightarrow{W_{+q}}=q\overrightarrow{E}· \overrightarrow{AC}\qquad(3)$

Similarly, work done by the force on $-q$ charge particle to bring from position $B$ to position $B'$→

$ \overrightarrow{W_{-q}}=\overrightarrow{F_{-q}}·\overrightarrow{BD}$

$ \overrightarrow{W_{-q}}=q\overrightarrow{E}· \overrightarrow{BD}\qquad (4)$

So the total work is done by the force on the dipole→

$ \overrightarrow{W}=\overrightarrow{W_{+q}}\:+\:\overrightarrow{W_{-q}}$

$\overrightarrow{W}=q\overrightarrow{E}·(\overrightarrow{AC}+\overrightarrow{BD})\qquad (5)$

From the figure, There is symmetry so

$ \overrightarrow{AC}=\overrightarrow{BD}$

So from equation $(5)$

$ \overrightarrow{W}=q\overrightarrow{E}·(2\overrightarrow{AC})$

$ \overrightarrow{W}=2q\overrightarrow{E}(\overrightarrow{AO}-\overrightarrow{CO})\qquad (6)$

From figure→

$ \left | \overrightarrow{AO} \right |=l$

$ \left | \overrightarrow{CO} \right |=l\:cos \theta$

Now substitute the values in equation (6). So equation (6) can be written as in magnitude form →

$ W=2qE(l-l\:cos\theta )$

$ W=2qEl(1-cos\theta )$

$ W=pE(1-cos\theta )$

The above expression shows that work is done on a rotating electric dipole in a uniform electric field.

Case (i):

If $\theta=0^{\circ}$, Then work done will be minimum

$W_{min}=0$

Case (ii):

If $\theta=90^{\circ}$, Then work done

$W=pE$

Case (iii):

If $\theta=180^{\circ}$, Then work done will be maximum

$W_{max}=2pE$

Read More