Statement of Bernoulli's Theorem:
When an ideal fluid (i.e incompressible and non-viscous Liquid or Gas) flows in streamlined motion from one place to another, then the total energy per unit volume (i.e Pressure energy + Kinetic Energy + Potential Energy) at each and every of its path is constant.
$P+\frac{1}{2}\rho v^{2} + \rho gh= constant$
Derivation of Bernoulli's Theorem Equation:
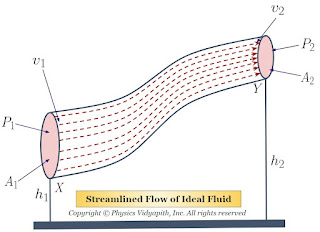
Let us consider that an incompressible and non-viscous liquid is flowing in streamlined motion through a tube $XY$ of the non-uniform cross-section.
Now Consider:
The Area of cross-section $X$ = $A_{1}$
The Area of cross-section $Y$ = $A_{2}$
The velocity per second (i.e. equal to distance) of fluid at cross-section $X$ = $v_{1}$
The velocity per second (i.e. equal to distance) of fluid at cross-section $Y$ = $v_{2}$
The Pressure of fluid at cross-section $X$ = $P_{1}$
The Pressure of fluid at cross-section $Y$ = $P_{2}$
The height of cross-section $X$ from surface = $h_{1}$
The height of cross-section $Y$ from surface = $h_{2}$
The work done per second by force on the liquid Entering the tube at $X$:
$W_{1}$ = Force $ \times $ Distance covered in one second
$W_{1}= P_{1} \times A_{1} \times v_{1} \quad \left( Force =Pressure \times Area \right)$
Similarly
The work done per second by force on the liquid leaving the tube at $Y$:
$W_{2}= P_{2} \times A_{2} \times v_{2}$
The net work done on the liquid:
$\Delta W=W_{1}-W_{2}$
$\Delta W= P_{1} \times A_{1} \times v_{1} - P_{2} \times A_{2} \times v_{2} \qquad(1)$
Now according to the principle of continuity:
$A_{1} v_{1} = A_{2} v_{2} = \frac{m}{\rho} \qquad(2)$
Now from equation $(1)$ and equation $(2)$
$\Delta W=\left( P_{1} -P_{2} \right) \frac {m}{\rho} \qquad(3)$
The kinetic energy of the fluid entering at $X$ in 1 second
$K_{1}=\frac{1}{2}mv_{1}^{2}$
The kinetic energy of the fluid leaving at $Y$ in 1 second
$K_{2}=\frac{1}{2}mv_{2}^{2}$
Therefore, The increase in kinetic energy
$\Delta K = K_{2}-K_{1}$
Now substitute the value of $K_{1}$ and $K_{2}$ in above equation then
$\Delta K = \frac{1}{2}mv_{2}^{2} - \frac{1}{2}mv_{1}^{2}$
$\Delta K = \frac{1}{2}m \left( v_{2}^{2} - v_{1}^{2} \right) \qquad(4)$
The potential energy of fluid at $X$
$U_{1}= mgh_{1}$
The potential energy of fluid at $Y$
$U_{2}= mgh_{2}$
Therefore, The decrease in potential energy
$\Delta U = U_{1}-U_{2}$
Now substitute the value of $U_{1}$ and $U_{2}$ in above equation then
$\Delta U = mgh_{1} - mgh_{2}$
$\Delta U = mg \left( h_{1} - h_{2} \right) \qquad(5)$
This increase in energy is due to the net work done on the fluid, i.e.
Net Work done = Net increase in energy
Net Work done $(\Delta W)$ = Net increase in Kinetic Energy $(\Delta K)$ - Net decrease in Potential Energy $(\Delta U)$
$\left( P_{1} -P_{2} \right) \frac {m}{\rho} = \frac{1}{2}m \left( v_{2}^{2} - v_{1}^{2} \right) - mg \left( h_{1} - h_{2} \right) $
$\left( P_{1} -P_{2} \right) = \frac{1}{2}\rho \left( v_{2}^{2} - v_{1}^{2} \right) -\rho g \left( h_{1} - h_{2} \right) $
$P_{1} + \frac{1}{2} \rho v_{1}^{2} + \rho g h_{1} = P_{2} + \frac{1}{2}\rho v_{2}^{2} + \rho g h_{2} $
$P + \frac{1}{2} \rho v^{2} + \rho g h = Constant $
This is Bernoulli's theorem equation.
Pressure Head, Velocity Head, and Gravitational Head of a Flowing Fluid:
According to Bernoulli's Theorem equation
$P + \frac{1}{2} \rho v^{2} + \rho g h = Constant $
Now dividing the above equation by $\rho g$, then we get
$\frac{P}{\rho g}+\frac{v^{2}}{2g}+ h = Constant$
Where
$\frac{P}{\rho g}$ = Pressure Head
$\frac{v^{2}}{2g}$ = Velocity Head
$h$ = Gravitational Head
The dimension of each of these three is the dimension of height. The sum of these heads is called the 'Total Head'
Therefore, Bernoulli's theorem may also state as follows:
In streamlined motion of an ideal fluid, the sum of pressure head, velocity head and gravitational head at any point is always constant.
When the fluid flows in a horizontal plane $(h_{1}=h_{2})$, then Bernoulli's equation
$P_{1} + \frac{1}{2} \rho v_{1}^{2} = P_{2} + \frac{1}{2}\rho v_{2}^{2} $
$\frac{P}{\rho g}+\frac{v^{2}}{2g} = Constant$