Definition and Expression of escape velocity of an object on the planet

Definition of Escape Velocity:

The minimum velocity, by which an object is thrown vertically in an upward direction and that object goes out from the gravitation field of the planet and does not come back, is called the escape velocity.

Deduction Escape Velocity Expression:

Let us consider the following:

The mass of the planet =$M$
The radius of the planet = $R$
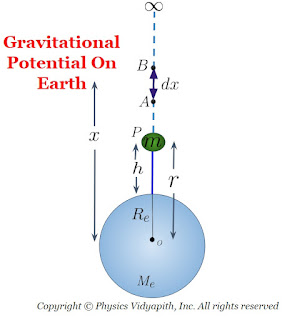
The mass of the object = $m$

The gravitational force on an object at position $P$ which is a distance $x$ from the surface of the planet

$F=G\frac{M m}{x^{2}} \qquad(1)$

The work done by the force to move the object a very small distance $dx$ from position $A$ to $B$

$W=F.dx$

$dw=G\frac{M m}{x^{2}}dx$

The total work done to move the object from the surface of the planet to infinity

$\int^{W}_{0}dw= \int^{\infty}_{R}G\frac{M m}{x^{2}}dx$

$\left[ w \right]^{W}_{0}=G M m \int^{\infty}_{R} \frac{dx}{x^{2}}$

On solving the above equation

$W=GM m \int^{\infty}_{R} \frac{dx}{x^{2}}$

$W=GM m \left[ -\frac{1}{x} \right]^{\infty}_{R}$

$W=GM m \left[ -\frac{1}{\infty} + \frac{1}{R} \right]$

$W=GM m \left[\frac{1}{R} \right]$

$W=\frac{G M m}{R}$

The above work done is given to the object in the form of kinetic energy to projectile from the surface of the planet to infinity. i.e.

$\frac{1}{2} m v^{2}_{e}= \frac{G M m}{R} $

Where $v_{e}$ is the escape velocity of the object.

$v^{2}_{e} = \frac{2G M m}{R}$

$v_{e} = \sqrt{\frac{2G M}{R}} \qquad(2)$

$v_{e} = \sqrt{\frac{2gR^{2}}{R}} \qquad \left(\because GM=gR^{2} \right)$

$v_{e} = \sqrt{2gR} \qquad(3)$

For earth put mass of the planet $M=M_{e}$ and $R=R_{e}$ in the above equation$(2)$ and equation$(3)$ and we get

$v_{e} = \sqrt{\frac{2G M_{e}}{R_{e}}} $

$v_{e} = \sqrt{2gR_{e}} $

Now substitute the value of the $g=9.8 m/s^{2}$ and radius of earth $R_{e}= 6.4 \times 10^{6} m$ then the escape velocity of the object

$v_{e}=11.2 m/s$

This is the escape velocity of the earth.

Now put $M=\frac{4}{3} \pi R^{3}$ in the above equation $(2)$ then we get

$v_{e} = \sqrt{\frac{2G \frac{4}{3} \pi R^{3}}{R}} $

$v_{e} = \sqrt{\frac{8 \pi \rho G R^{2}}{3}} \qquad(4)$

From the equation $(2)$, $(3)$, and $(4)$ we can conclude that

1.) The escape velocity of the object does not depend on the mass of the object.

2.) The escape velocity of the object is depend upon the mass and radius of the planet.

3.) If the velocity of the object is less than the escape velocity, then the object will reach a certain height and may either move in an orbit around the earth or may fall back to the planet.

4.) If the velocity of projection $(v)$ of the body from the surface of a planet is greater than the escape velocity $v_{e}$ of the planet, the body will escape out from the gravitational field of that planet and will move the interstellar space with velocity $v'$ which can be obtained by using the conservation of energy.

$\frac{1}{2}mv^{2}+\left( -\frac{GMm}{R} \right)= \frac{1}{2}mv'^{2}+0$

$\frac{1}{2}mv^{2}+\left( -\frac{GMm}{R} \right)= \frac{1}{2}mv'^{2}$

$v'^{2}= v^{2} - \frac{2GM}{R}$

$v'^{2}= v^{2} - v^{2}_{e} \qquad \left( \because v^{2}_{e} = \frac{2GM}{R} \right)$

$v'= \sqrt{v^{2} - v^{2}_{e}}$

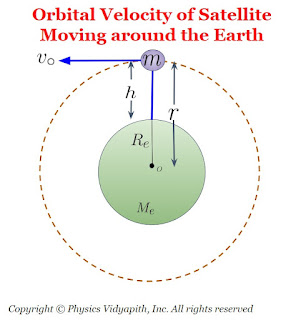
The relation between orbital velocity and escape velocity of an object:

We know that the orbital velocity of any object revolving near the planet is

$v_{\circ} = \sqrt{gR} \qquad(1)$

The escape velocity of an object which is placed on the planet is

$v_{e} = \sqrt{2gR} \qquad(2)$

From the above equation $(1)$ and equation $(2)$, we get

$v_{e} = \sqrt{2} v_{\circ}$

Alternative Method to Derive Expression for Escape Velocity:

The potential energy of an object on the surface of the planet

$U=-\frac{GMm}{R}$

If the object is thrown vertically in the upward direction with escape velocity $v_{e}$, then the kinetic energy of the object:

$K=\frac{1}{2}mv_{e}^{2}$

We know that the total energy of the object is zero at infinity and then

$K+U=0$

Now substitute the value of $K$ and $U$ in the above equation

$\left( \frac{1}{2}mv_{e}^{2} \right)+\left( -\frac{GMm}{R} \right)=0$

$ \frac{1}{2}mv_{e}^{2} -\frac{GMm}{R} =0$

$ \frac{1}{2}mv_{e}^{2} = \frac{GMm}{R} $

$ \frac{1}{2}v_{e}^{2} = \frac{GM}{R} $

$v_{e}^{2} = \frac{2GM}{R} $

$v_{e} = \sqrt {\frac{2GM}{R}} $

$v_{e} = \sqrt{\frac{2gR^{2}}{R}} \qquad \left(\because GM=gR^{2} \right)$

$v_{e} = \sqrt{2gR} $

Read More

Variation of Acceleration Due to Gravity

Variation in Gravitational Acceleration:

The value of $g$ varies above and below the surface of the earth. It also changes with the latitude at different places and due to the rotation of the earth about its axis. The earth is not a perfect sphere but is approximately an ellipsoid. The radius of the earth is more at the equator and lesser at the poles. The acceleration due to gravity also changes due to the shape of the earth.

1.) Effect of Altitude on Acceleration due to Gravity
2.) Effect of depth below the earth's surface on Acceleration due to Gravity
3.) Effect of the shape of the earth 4.) Effect of rotation about its own axis

1.) Effect of Altitude on Acceleration due to Gravity:

Let us consider: The mass of the earth = $M_{e}$
The radius of the earth = $R_{e}$
A satellite is moving around the earth from the surface of the earth at height= $h$

The gravitational acceleration on the surface of the earth at point $A$

$g=\frac{GM_{e}}{R_{e}^{2}} \qquad (1.1)$

The gravitational acceleration on the altitude $h$ from the surface of the earth at point $B$

$g'=\frac{GM_{e}}{\left( R_{e} + h \right)^{2}} \qquad(1.2)$

Now divide equation $(1.2)$ by equation $(1.1)$

$\frac{g'}{g}= \frac{\frac{GM_{e}}{\left( R_{e} + h \right)^{2}}}{\frac{GM_{e}}{R_{e}^{2}}}$

$\frac{g'}{g}= \frac{R_{e}^{2}}{\left( R_{e} + h \right)^{2}}$

$\frac{g'}{g}= \frac{R_{e}^{2}}{R_{e}^{2} \left( 1 + \frac{h}{R_{e}} \right)^{2}}$

$\frac{g'}{g}= \frac{1}{ \left( 1 + \frac{h}{R_{e}} \right)^{2}}$

$\frac{g'}{g}= \left( 1 + \frac{h}{R_{e}} \right)^{-2}$

Now apply the binomial theorem

$\frac{g'}{g}= 1 - \frac{2h}{R_{e}} + \frac{3h^{2}}{R_{e}^{2}}$

Here $h \lt R_{e}$ then $h^{2} \lt \lt R_{e}^{2}$ so neglect the term of higher power of $\frac{3h^{2}}{R_{e}^{2}}$. Therefore we get

$\frac{g'}{g}= 1 - \frac{2h}{R_{e}} $

$g'= \left( 1 - \frac{2h}{R_{e}} \right) g $

From the above equation it is clear that the value $\left( 1 - \frac{2h}{R_{e}} \right) \lt 1$ then

$g' \lt g$

So, the gravitational acceleration $g$ decreases above the earth's surface.

2.) Effect of depth below the earth's surface on Acceleration due to Gravity:

Let us consider:
The mass of the earth = $M_{e}$
The mass of the earth at depth $h$ from the surface of the earth = $M'_{e}$
The radius of the earth = $R_{e}$

The gravitational acceleration on the surface of the earth at point $A$

$g=\frac{GM_{e}}{R_{e}^{2}} \qquad (2.1)$

The gravitational acceleration at point $B$ on the depth $h$ from the surface of the earth

$g'=\frac{GM'_{e}}{\left( R_{e} - h \right)^{2}} \qquad(2.2)$

Now divide equation $(2.2)$ by equation $(2.1)$

$\frac{g'}{g}= \frac{\frac{GM'_{e}}{\left( R_{e} - h \right)^{2}}}{\frac{GM_{e}}{R_{e}^{2}}}$

$\frac{g'}{g}= \frac{R_{e}^{2}}{\left( R_{e} - h \right)^{2}} \left( \frac{M'_{e}}{M_{e}} \right) \qquad(2.3)$

If $\rho$ is the density of the earth the total mass of the earth and the mass of the earth at depth $h$

$M_{e}=\frac{4}{3}\pi R_{e}^{3} \rho$

$M'_{e}=\frac{4}{3}\pi \left ( R_{e}-h\right)^{3} \rho$

Now subtitute the value of $M_{e}$ and $M'_{e}$ in equaion $(2.3)$

$\frac{g'}{g}= \frac{R_{e}^{2}}{\left( R_{e} - h \right)^{2}} \left( \frac{\frac{4}{3}\pi \left ( R_{e}-h\right)^{3} \rho}{\frac{4}{3}\pi R_{e}^{3} \rho} \right) $

$\frac{g'}{g}= \frac{\left( R_{e} - h \right)}{R_{e}}$

$\frac{g'}{g}= \left( 1 - \frac{h}{R_{e}} \right)$

$g'= \left( 1 - \frac{h}{R_{e}} \right)g$

From the above equation it is clear that the value $\left( 1 - \frac{h}{R_{e}} \right) \lt 1$ then

$g' \lt g$

So, the gravitational acceleration $g$ decreases below the earth's surface.

3.) Effect of the shape of the earth:

Earth is not a perfect sphere. It is flattened at the poles and bulges out at the equator. The equatorial radius $R_{E}$ of the earth is about $21 Km$ Then greater than the polar radius $R_{P}$. Now from the equation $g=\frac{GM}{R^{2}}$ $\left (i.e. g \propto \frac{1}{R^{2}} \right)$, we can conclude that the higher radius has less gravitational acceleration because of that the value of $g$ is least at equator and maximum at the pole.

4.) Effect of rotation about its own axis:

Latitude at a plane is defined as the angle at which the line joining the place to the centre of the earth, makes with the equatorial plane. It is generally denoted by the $\lambda$.

From the figure given below, the latitude at a place $P = \angle OPC = \lambda$

Consider earth is in a perfect sphere of mass $M_{e}$, radius $R_{e}$ with centre $O$. The whole mass of the earth is supposed to be concentrated at the centre $O$. As the earth rotates about its polar axis from west to east, every particle lying on its surface moves along a horizontal circle with the same angular velocity as that of the earth. The centre of each circle lies on the polar axis.

Let us consider, a particle of mass $m$ at a place $P$ of latitude $\lambda$. If the earth is rotating about its polar axis $NS$ with constant angular velocity $\omega$, then the particle also rotates and describes a horizontal circle of radius $r$, Where

$r=PC=OP \: cos\lambda = R \: cos\lambda \qquad (3.1)$

The centrifugal force acting on the particle at $P$ is $m\: r \: \omega^{2}$. It acts along $PA$ directed away from the centre $C$ of the circle of rotation.

The true weight of the particle = $mg$

The centrifugal force at P = $m\: r \: \omega^{2}$

So the resultant of true weight and centrifugal force is $mg'$ can be found by Using the parallelogram law of the forces i.e

$mg'=\sqrt{(mg)^{2}+(mr\omega^{2})^{2}+2(mg)(mr\omega^{2})cos (180^{\circ}- \lambda)}$

$g'=\sqrt{(g)^{2}+(r\omega^{2})^{2}+2(g)(r\omega^{2})cos\lambda)}$

$g'=\sqrt{(g)^{2}+(\omega^{2} R \: cos \lambda )^{2}+2(g)( \omega^{2} R \: cos \lambda )cos\lambda)} \qquad \left( \because r=R \: cos \lambda \right)$

$g'=g \left( 1 + \frac{R^{2}\omega^{4}}{g^{2}} cos^{2} \lambda - \frac{2R \omega^{2}}{g} cos^{2} \lambda)\right)^{\frac{1}{2}}$

Here the value of $\frac{R \omega^{2}}{g}$ is very small, therefore the terms with its squares and of higher power can be neglected. So the above equation can be written as:

$g'=g \left( 1 - \frac{2R \omega^{2}}{g} cos^{2} \lambda)\right)^{\frac{1}{2}}$

Now apply the binomial theorem, and we get

$g'=g \left( 1 - \frac{1}{2}\frac{2R \omega^{2}}{g} cos^{2} \lambda)\right)$

$g'=g \left( 1 - \frac{R \omega^{2}}{g} cos^{2} \lambda)\right)$

$g'= \left( g - R \omega^{2} cos^{2} \lambda\right) \qquad(3.2)$

As, $cos \lambda$ and $\omega$ are positive, therefore $g' \lt g$. Thus from the above equation, it is clear that acceleration due to gravity:

i.) Decreases on account of the rotation of the earth
ii.) Increases with the increase in the latitude of the place.

At equator,
$\lambda = 0^{\circ}$
$g'=p_{e}$
Then from above equation $(3.2)$,

$g_{e}=g-R\omega^{2}$

Clearly, $g_{e}$ is minimum.

At pole,
$\lambda = 90^{\circ}$
$g'=g_{p}$
Then from above equation $(3.2)$,

$g_{p}=g-R\omega^{2 (0)}$

$g_{P}=g$

Clearly, $g_{p}$ is maximum.

Hence, the value of acceleration due to gravity is minimum at the equator and maximum at the poles. The value of acceleration due to gravity at the poles will remain unchanged whether the earth is at rest or rotating.

The difference in the value of acceleration due to gravity at the pole and equator:

We know that:

Acceleration due to gravity at the equator is

$g_{e}=g-R\omega^{2}$

Acceleration due to gravity at the pole is

$g_{p}=g$

The difference in gravitational acceleration at the equator and pole

$g_{p} - g_{e}= g - \left(g-R\: \omega^{2} \right)$

$g_{p} - g_{e}= R\: \omega^{2}$

$g_{p} - g_{e}= R\: \left( \frac{2 \pi }{T}\right)^{2}$

Now put $T=24 \times 60 \times 100$

$g_{p} - g_{e} \approx 0.034 m/sec^{2}$

Read More

Total energy of an orbiting Satellite and its Binding Energy

Definition: The total energy of a satellite revolving around the planet is the sum of kinetic energy (i.e. due to orbital motion) and potential energy (i.e. due to the gravitational potential energy of the satellite).

Derivation of the total energy of the satellite revolving around the planet:

Let us consider

The mass of the satellite = $m$

The mass of the planet = $M$

The satellite revolving around a planet at distance from the center of the planet = $r$

The radius of planet =$R$

The potential energy of the satellite is

$U=-\frac{G \: M \: m}{r} \qquad(1)$

The kinetic energy of the satellite is

$K=\frac{1}{2}m v_{e}^{2}$

$K=\frac{1}{2} m \left( \sqrt{\frac{G \: M}{r}} \right)^{2} \qquad \left( \because v_{e}^{2}=\sqrt{\frac{G \: M}{r}} \right)$

$K=\frac{1}{2} \left( \frac{G \: M \: m}{r} \right) \qquad(2)$

The total energy of the satellite is

$E= K+U$

Now substitute the value of the kinetic energy and potential energy in the above equation from equation $(1)$ and equation $(2)$

$E= \frac{1}{2} \left( \frac{G \: M \: m}{r} \right)+ \left( -\frac{G \: M \: m}{r} \right)$

$E= -\frac{1}{2} \left( \frac{G \: M \: m}{r} \right)$

$E= -\frac{1}{2} \left( \frac{G \: M \: m}{R+h} \right) \left( \because r=R+h \right)$

This is the expression for the total energy of the satellite revolving around the planet. The above expression shows that the total of a revolving satellite is negative.

The total energy of the orbiting satellite around the Earth:

Put $M=M_{e}$ and $R=R_{e}$ then

$E= -\frac{1}{2} \left( \frac{G \: M_{e} \: m}{R_{e}+h} \right) \left( \because r=R_{e}+h \right)$

$E= -\frac{1}{2} \left( \frac{g \: R_{e}^{2} \: m}{R_{e}+h} \right) \left( \because GM_{e}=g R_{e}^{2} \right)$

If the satellite revolves around near the earth (i.e. $h=0$) then the total energy of the satellite

$E= -\frac{1}{2} \left( \frac{g \: R_{e}^{2} \: m}{R_{e}+0} \right)$

$E= -\frac{1}{2} \left( \frac{g \: R_{e}^{2} \: m}{R_{e}} \right)$

$E= -\frac{1}{2} \left( g \: R_{e} \: m \right)$

Binding Energy of the Satellite:

The minimum amount of energy required to free the revolving satellite around the planet from its orbit is called the binding energy of the revolving satellite.

We know that the total energy of the revolving satellite is

$E= -\frac{1}{2} \left( \frac{G \: M \: m}{R+h} \right)$

The total energy of the satellite at infinity is zero. When an equal positive amount of energy of the total energy of the satellite is given to the satellite, the total energy of the satellite is become zero and the planet leaves its orbit. So this total positive energy is called the binding energy of the satellite. i.e.

$E= +\frac{1}{2} \left( \frac{G \: M \: m}{R+h} \right)$

The binding energy of the orbiting satellite around the earth

$E= +\frac{1}{2} \left( \frac{G \: M_{e} \: m}{R_{e}+h} \right)$

If a satellite revolves around near earth ($h=0$) then binding energy

$E= +\frac{1}{2} \left( \frac{G \: M_{e} \: m}{R_{e}} \right)$

Read More

Expression for Orbital velocity of Satellite and Time Period

Orbital Velocity of Satellite:

When any satellite moves about the planet in a particular orbit then the velocity of the satellite is called the orbital velocity of the satellite.

Expression for Orbital Velocity of Satellite:

Let us consider:

The mass of the satellite = $m$

The mass of planet= $M$

The radius of Planet =$R$

The satellite is moving about the planet at height=$h$

The satellite is moving about the planet with orbital velocity=$v_{\circ}$

The distance from the center of the planet to satellite=$r$

The force of gravitation between the planet and the satellite

$F=G \frac{M \: m}{r^{2}} \qquad(1)$

This force work act as a centripetal force to revolve the satellite around the planet i.e.

$F=\frac{m v_{\circ}^{2}}{r} \qquad(2)$

From the above equation $(1)$ and equation $(2)$, we get

$\frac{m v_{\circ}^{2}}{r} = G \frac{M \: m}{r^{2}}$

$v_{\circ}= \sqrt{\frac{G \: M }{r}}$

Where $r=R+h$ then

$v_{\circ}= \sqrt{\frac{G \: M }{R+h}} \qquad(3)$

This is the equation of the orbital velocity of the satellite.

If any satellite revolves around the earth then the orbital velocity

$v_{\circ}= \sqrt{\frac{G \: M_{e} }{R_{e}+h}}$

$v_{\circ}= \sqrt{\frac{gR_{e}^{2}}{R_{e}+h}} \qquad \left( \because G \: M_{e} = gR_{e}^{2} \right)$

$v_{\circ}= R_{e} \sqrt{\frac{g}{R_{e}+h}} $

This is the equation of the orbital velocity of a satellite revolving around the earth.

If the satellite is orbiting very close to the surface of the earth ( i.e $h=0$) then the orbital velocity

$v_{\circ}= R_{e} \sqrt{\frac{g}{R_{e}+0}} $

$v_{\circ}= \sqrt{g R_{e}} $

Now subtitute the value of radius of earth (i.e $R_{e}=6.4 \times 10^{6} \: m$) and gravitational accelertaion ($g=9.8 \:m/sec^{2}$) then orbital velocity

$v_{\circ}=7.92 \: Km/sec$

The time period of Revolving Satellite:

The time taken by satellite to complete on revolution around the planet is called the time period of the satellite.

Let us consider the time period of the revolving satellite is $T$ Then

$T= \frac{Distance \: covered \: by \: Satellite \: in \: one \: revolution}{Orbital \: Velocity}$

$T= \frac{2 \pi r}{v_{\circ}}$

$T= \frac{2 \pi \left( R+h \right)}{v_{\circ}}$

$T= \frac{2 \pi \left( R+h \right)}{v_{\circ}}$

Now subtitute the value of orbital velocity $v_{\circ}$ from equation $(3)$ in above equation then

$T= \frac{2 \pi \left( R+h \right)}{\sqrt{\frac{G \: M }{R+h}}}$

$T= 2 \pi \sqrt{ \frac{ \left( R+h \right)^{3}}{G M}}$

This is the equation of the time period of the revolution of satellites.

If a satellite revolves around the earth then the time period

$T= 2 \pi \sqrt{ \frac{ \left( R_{e}+h \right)^{3}}{G M_{e}}}$

$T= 2 \pi \sqrt{ \frac{ \left( R_{e}+h \right)^{3}}{g R_{e}^{2}}} \qquad \left( \because G \: M_{e} = gR_{e}^{2} \right)$

This is the equation of the time period of revolution of satellite revolving around the earth.

If the satellite revolves very nearly around the earth (i.e $h=0$) then the time period of the satellite from the above equation

$T= 2 \pi \sqrt{ \frac{ \left( R_{e}+0 \right)^{3}}{g R_{e}^{2}}} $

$T= 2 \pi \sqrt{ \frac{ R_{e}}{g}} $

$T= 84.6 \: min $

Read More

Derivation of Gravitational Potential Energy due to Point mass and on the Earth

Definition of Gravitational Potential Energy:

When an object is brought from infinity to a point in the gravitational field then work done acquired by the gravitational force is stored in the form of potential energy which is called gravitational potential energy.

Let us consider, An object of mass $m$ brought from infinity to a point in the gravitational field. If work done acquired by force is $W$ then gravitational potential energy

$U=W_{\infty \rightarrow r}$

Derivation of Gravitational Potential energy due to a Point mass:

Let us consider,
The mass of the point object (i.e point mass)=$m$
The mass of the object that produces the gravitational field = $M$

If the point mass $m$ is at a distance $x$ then the gravitational force between the objects is

$F=G \frac{M \: m}{x^{2}} \qquad(1)$

If the point mass moves a very small distance element $dx$ that is at distance $x$ from point $O$ then the work done to move the point object from point $B$ to $A$

$dw=F.dx$

Now substitute the value of $F$ from equation $(1)$ in above equation

$dw=G \frac{M \: m}{x^{2}}.dx$

Therefore, the work done to bring the point mass from infinity to point $P$ that is at distance $r$ from point $O$ then work done to move the point object from infinity ($\infty$) to point $P$

$\int_{0}^{W} dw = \int_{\infty}^{r} G \frac{M \: m}{x^{2}}.dx $

$ [w]_{0}^{W} = G\: M\: m \int_{\infty}^{r} \frac{1}{x^{2}}.dx $

$ [W-0] = G\: M\: m [-\frac{1}{x} ]_{\infty}^{r} $

$ W = G\: M\: m [\left(-\frac{1}{r}\right) - \left(-\frac{1}{\infty}\right)]$

$ W = -\frac{G\: M\: m }{r} \qquad \left( \because \frac{1}{\infty} =0 \right)$

$ W = -\frac{G\: M\: m }{r} $

This work done by the force is stored in the form of potential energy i.e

$U=W$

$U=-\frac{G\: M\: m }{r}$

Thus the above equation represents the gravitational potential energy of an object at point $P$

Gravitational Potential Energy on Earth:

Let us consider, The mass of Earth = $M_{e}$
The radius of earth = $R_{e}$
The mass of the object = $m$
The distance from centre $O$ of the earth to point $P$ = $r$
The distance from the surface of the earth to point $P$ = $h$

If the object is at a distance $x$ then the gravitational force is

$F=G \frac{M_{e} \: m}{x^{2}} \qquad(1)$

If the object moves a very small distance element $dx$ that is at distance $x$ from centre point $O$ of the earth then the work done to move an object from point $B$ to $A$

$dw=F.dx$

Now substitute the value of $F$ from equation $(1)$ in above equation

$dw=G \frac{M_{e} \: m}{x^{2}}.dx$

Therefore, the work done to bring the object from infinity to point $P$ that is at distance $r$ from centre point $O$ of the earth then the work done to move an object from infinity ($\infty$) to point $P$

$\int_{0}^{W} dw = \int_{\infty}^{r} G \frac{M_{e} \: m}{x^{2}}.dx $

$ [w]_{0}^{W} = G\: M_{e}\: m \int_{\infty}^{r} \frac{1}{x^{2}}.dx $

$ [W-0] = G\: M_{e}\: m [-\frac{1}{x} ]_{\infty}^{r} $

$ W = G\: M_{e}\: m [\left(-\frac{1}{r}\right) - \left(-\frac{1}{\infty}\right)]$

$ W = -\frac{G\: M_{e}\: m }{r} \qquad \left( \because \frac{1}{\infty} =0 \right)$

$ W = -\frac{G\: M_{e}\: m }{r} $

The above equaton shows that the work done by force is stored in the form of gravitational potential energy i.e.

$U=W$

$ U = -\frac{G\: M_{e}\: m }{r}$

Where $r=R_{e}+h$, then above equation can be written as

$U = -\frac{G\: M_{e}\: m }{R_{e}+h} \qquad(2)$

This is the equation of the gravitational potential energy at point $P$. The other form of the above equation i.e

$U = -\frac{g R_{e}^{2} \: m }{R_{e}+h} \qquad \left( \because GM_{e}= g R_{e}^{2} \right)$

If the object is placed on the surface of the earth then $h=0$. So gravitational potential energy on the surface of the earth
$U=-\frac{G \: M_{e} \: m}{R_{e}}$

This is the equation of the gravitational potential energy of an object placed on the surface of the earth.

$U=-\frac{g R_{e}^{2} m}{R_{e}} \qquad \left( \because GM_{e}= g R_{e}^{2} \right)$

$U=-g R_{e} m$ This is another form of the gravitational potential energy of an object placed on the surface of the earth.

Note:

We know that the gravitational potential energy at any point from above the surface of the earth

$U = -\frac{G\: M_{e}\: m }{R_{e}+h} $

$U = V m \qquad \left( \because V= -\frac{G\: M_{e}\: }{R_{e}+h} \right)$

$U = Gravitational \: Potential \times \: mass \: of \: an \: object$

Read More

Derivation of Gravitational Potential due to Point mass and on the Earth

Definition of Gravitational Potential:

When an object is brought from infinity to a point in the gravitational field then work done acquired by the gravitational force is called gravitational potential.

Let us consider, An object of mass $m$ brought from infinity to a point in the gravitational field. If work done acquired by force is $W$ then gravitational potential

$V=-\frac{W}{m}$

Derivation of Gravitational Potential due to a Point mass:

Let us consider,
The mass of the point object (i.e point mass)=$m$
The mass of the object that produces the gravitational field = $M$

If the point mass $m$ is at a distance $x$ then the gravitational force between the objects is

$F=G \frac{M \: m}{x^{2}} \qquad(1)$

If the point mass moves a very small distance element $dx$ that is at distance $x$ from point $O$ then the work done to move the point object from point $B$ to $A$

$dw=F.dx$

Now substitute the value of $F$ from equation $(1)$ in above equation

$dw=G \frac{M \: m}{x^{2}}.dx$

Therefore, the work done to bring the point mass from infinity to point $P$ that is at distance $r$ from point $O$ then work done to move the point object from infinity ($\infty$) to point $P$

$\int_{0}^{W} dw = \int_{\infty}^{r} G \frac{M \: m}{x^{2}}.dx $

$ [w]_{0}^{W} = G\: M\: m \int_{\infty}^{r} \frac{1}{x^{2}}.dx $

$ [W-0] = G\: M\: m [-\frac{1}{x} ]_{\infty}^{r} $

$ W = G\: M\: m [\left(-\frac{1}{r}\right) - \left(-\frac{1}{\infty}\right)]$

$ W = -\frac{G\: M\: m }{r} \qquad \left( \because \frac{1}{\infty} =0 \right)$

$ W = -\frac{G\: M\: m }{r} $

$\frac{W}{m} = -\frac{G\: M }{r} $

$ V = -\frac{G\: M}{r} \qquad \left( \because V=\frac{W}{m} \right)$

$ V = -\frac{G\: M}{r}$

Thus the above equation represents the gravitational potential at point $P$

Gravitational Potential on Earth:

Let us consider, The mass of Earth = $M_{e}$
The radius of earth = $R_{e}$
The mass of the object = $m$
The distance from centre $O$ of the earth to point $P$ = $r$
The distance from the surface of the earth to point $P$ = $h$

If the object is at a distance $x$ then the gravitational force is

$F=G \frac{M_{e} \: m}{x^{2}} \qquad(1)$

If the object moves a very small distance element $dx$ that is at distance $x$ from centre point $O$ of the earth then the work done to move an object from point $B$ to $A$

$dw=F.dx$

Now substitute the value of $F$ from equation $(1)$ in above equation

$dw=G \frac{M_{e} \: m}{x^{2}}.dx$

Therefore, the work done to bring the object from infinity to point $P$ that is at distance $r$ from centre point $O$ of the earth then the work done to move an object from infinity ($\infty$) to point $P$

$\int_{0}^{W} dw = \int_{\infty}^{r} G \frac{M_{e} \: m}{x^{2}}.dx $

$ [w]_{0}^{W} = G\: M_{e}\: m \int_{\infty}^{r} \frac{1}{x^{2}}.dx $

$ [W-0] = G\: M_{e}\: m [-\frac{1}{x} ]_{\infty}^{r} $

$ W = G\: M_{e}\: m [\left(-\frac{1}{r}\right) - \left(-\frac{1}{\infty}\right)]$

$ W = -\frac{G\: M_{e}\: m }{r} \qquad \left( \because \frac{1}{\infty} =0 \right)$

$ W = -\frac{G\: M_{e}\: m }{r} $

$\frac{W}{m} = -\frac{G\: M_{e} }{r} $

$ V = -\frac{G\: M_{e}}{r} \qquad \left( \because V=\frac{W}{m} \right)$

$ V = -\frac{G\: M_{e}}{r}$

Where $r=R_{e}+h$, then above equation can be written as

$V=-\frac{G \: M_{e}}{R_{e}+h} \qquad(2)$

This is the equation of gravitational potential at point $P$. The other form of the above equation i.e

$V=-\frac{g R_{e}^{2}}{R_{e}+h} \qquad \left( \because GM_{e}= g R_{e}^{2} \right)$

If the object is placed on the surface of the earth then $h=0$. So gravitational potential on the surface of the earth

$V=-\frac{G \: M_{e}}{R_{e}}$

This is the equation of gravitational potential on the surface of the earth. The other form of the above equation is

$V=-\frac{g R_{e}^{2}}{R_{e}} \qquad \left( \because GM_{e}= g R_{e}^{2} \right)$

$V=-g R_{e}$

Read More

Gravitational field, Intensity of Gravitational field and its expression

Definition of Gravitational Field:

The region around an object in which another object experiences a gravitational force then the region of that object is called the gravitational field.

Gravitational Field Intensity:

The force applied per unit mass of an object that is placed in the gravitational field is called the intensity of the gravitational field.

$\overrightarrow{E}=- \frac{G \: M}{r^{2}} \hat{r}$

The Expression for gravitational field intensity:

Let us consider
The mass of a lighter object that experience the force = $m$
The mass of a heavy object that produces the gravitational field= $M$
The distance between the objects = $r$

The gravitational force between the objects is

$F=G\frac{M\:m}{r^{2}} \qquad(1)$

Now the force per unit mass i.e Gravitational field intensity

$E=-\frac{F}{m} \qquad (2)$

Here the negative indicates that the direction of force is opposite to $\hat{r}$

The vector form of the gravitational field intensity

$\overrightarrow{E}=-\frac{F}{m} \hat{r}$

Where $\hat{r} \left (=\frac{\overrightarrow{r}}{r} \right)$ is the unit vector along the $\overrightarrow{r}$

Now substitute the value of $F$ in the above equation $(2)$. Therefore we get,

$E=-G \frac{M\:m}{m r^{2}}$

$E=- \frac{G \: M}{r^{2}}$

The vector form of the above equation

$\overrightarrow{E}=- \frac{G \: M}{r^{2}} \hat{r}$

Read More

Deduction of Newton's Law of gravitation from Kepler's Law

Deduction of Newton's Law of gravitational force from Kepler's Law:

Let us consider:
The mass of a planet = $m$
The radius of the circular path of a planet=$r$
The mass of the sun = $M$
The velocity of the planet = $v$
The time of the revolution=$T$

The attraction force between the planet and the sun is achieved by the centripetal force i.e

$F=\frac{m v^{2}}{r} \qquad(1)$

The orbital velocity of the planet:

$v=\frac{Circumference \: of \: the \: circular \: path}{Time \: period}$

$v=\frac{2\pi r}{T} \qquad(2)$

From equation $(1)$ and equation $(2)$, we get

$F=\frac{m}{r} \left( \frac{2\pi r}{T} \right)^{2}$

$F=\frac{4 \pi^{2} mr}{T^{2}} \qquad(3)$

According to Kepler's third law i.e

$T^{2}=Kr^{3} \qquad(4)$

From equation$(3)$ and equation$(4)$, we get

$F=\frac{4 \pi^{2}mr}{Kr^{3}}$

$F=\frac{4 \pi^{2}}{K}\frac{mr}{r^{3}}$

$F=\frac{4 \pi^{2}}{K}\frac{m}{r^{2}} \qquad(5)$

The source of this force is the sun. So R.H.S of equation $(5)$ should be related to the sun. Since $m$ and $r$ are related to the planet. So the quantity $\frac{4 \pi^{2}}{K}$ should be related to some constant of the sun. Let $\frac{4 \pi^{2}}{K}$ be proportional to the mass of the sun. i.e

$\frac{4 \pi^{2}}{K m} \propto M$

$\frac{4 \pi^{2}}{K m} = G M $

Here $G$ is the proportionality constant and it is called the universal gravitation constant. Now substitute the $\frac{4 \pi^{2}}{K m} = G M$ in equation $(5)$. then we get

$F=G \frac{M m}{r^{2}}$

The above equation represents the force of attraction between the sun and the planet. It is also known as Newton's law of gravitational force.

Read More

Kepler's Laws of Planetary Motion

Kepler's Laws →

Kepler's found important uniformity in the motion of the planets. This uniformity is known as "Kepler's Laws of planetary motion". There are basically three laws →

1. First law (Law of orbits)


2. Second Law (Law of Areal Speed)


3. Third Law (Law of Periods)

First law (Law of orbits) →

All the planets move around the sun in elliptical path and the sun is at the one foci of the ellipse.

Second Law (Law of Areal Speed) →

A line joining the any planet to sun sweeps out equal areas in equal interval of of times. i.e The areal speed of the planets remains constant.

According to the second law, When the planet is farthest from the sun, then its speed is maximum, and when it is nearest the sun, then its speed is maximum.

Planetary Motion

From the above figure, A planet is moving around the sun from $A$ to $B$ in a given time interval, and from $C$ to $D$ in the same time interval, then according to the law of areal speed, the areas $ASB$ and $CSD$ will be equal with respect to the same time-interval

Proof →

Let us consider, A planet moves the angle $d\theta$ from $A$ to $B$ in the infinitesimal interval of time $dt$, then the area swept out by radial line $SA$ is

$dA$= Area of the curved $\Delta$ $SAB$

$dA \approx \frac{1}{2} \left( AB \times SA \right)$

$dA \approx \frac{1}{2} \left( r \: d\theta \times r \right)$

$dA \approx \frac{1}{2} \left( r^{2} \: d\theta \right)$

Thus, the instantaneous areal speed of the planets is

$\frac{dA}{dt}=\frac{1}{2} r^{2} \frac{d \theta}{dt}$

$\frac{dA}{dt}=\frac{1}{2} r^{2} \omega \qquad(1)$

Where $\omega$ → The angular speed of the planet.

We know that

$J=I \: \omega$

Where $I$ is the instantaneous moment of inertia of the planet about the Sun $S$.

$J=m \: r^{2} \: \omega \qquad(2)$

Where $m$ is the mass of the planet. Now substitute the value of $r^{2} \: \omega$ from equation $(2)$ in equation $(1)$.

$\frac{dA}{dt}=\frac{J}{2m} \left( Constant \right)$

From the above equation, The areal speed $\frac{dA}{dt}$ of the planet is constant which is Kepler's Second Law. The above equation shows that the angular momentum of the planet is constant. i.e. The angular momentum of any planet is conserved.

Third Law (Law of Periods) →

The square of the time period of one complete revolution of any planet around the sun is directly proportional to the cube of the semi-major axis of its elliptical orbit.

Path of the Planet

Proof →

Let $a$ and $b$ be the semi-major and semi-minor axes of the ellipse, then the area of the ellipse will be $\pi ab$. Let $T$ is the period of one complete revolution of any planet, then

$T=\frac{Area \: of \: the \: ellipse}{Areal \: Speed}$

$T=\frac{\pi a b}{\frac{J}{2m}}$

$T=\frac{2\pi a b m}{J}$

$T^{2}=\frac{4 \pi^{2} a^{2} b^{2} m^{2}}{J^{2}}$

Let $l$ be the semi-latus rectum of the elliptical orbit i.e. $l=\frac{b^{2}}{a}$. Then we get the above equation which can be written as

$T^{2}=\frac{4 \pi^{2} m^{2} a^{3} l }{J^{2}}$

$T^{2} \propto a^{3} $

Where $\frac{4 \pi^{2} m^{2} l }{J^{2}}$ is constant.

From the above equation, It is clear that the larger the distance of a planet from the sun, the larger will be its period of revolution around the sun. The period of revolution of the nearest planet to the sun i.e. Mercury is $88$ days, while that of the faraway planet from the sun i.e. Pluto is $248$ years.

Read More

Relation between gravitational acceleration and gravitational force

Relation between $g$ and $G$ →

Let us consider:
The mass of earth = $M_{e}$
The radius of earth = $R_{e}$
The mass of the object = $m$

If the object is placed on the surface of the earth then the gravitational force on the object is →

$F=G \frac{M_{e} m}{R_{e}^{2}} \qquad(1)$

The force on the object due to gravitational acceleration is →

$F=mg \qquad(2)$

From equation $(1)$ and equation $(2)$

$mg=G \frac{M_{e} m}{R_{e}^{2}}$

$g=G \frac{M_{e}}{R_{e}^{2}}$

$G M_{e}=g R_{e}^{2}$

Read More

Newton's law for Gravitational Force

Gravitational Force →

Newton's Gravitational Law statement is a combination of three individual statements. These are

1. The force between the two-particle is directly proportional to the product of their masses i.e.
   
   
   
   $F \propto m_{1} \: m_{2} \qquad(1)$
   
   
   Where $m_{1}$ & $m_{2}$ are the masses of the particles.


2. The force between the two-particle is inversely proportional to the square of the distance between them i.e.
   
   
   
   $F \propto \frac{1}{r^{2}} \qquad(2)$
   
   
   Where $r$ is the distance between the particles.


3. This force always acts between the line joining the masses.

From the above the equation $(1)$ and equation $(2)$

$F\propto \frac{m_{1} \: m_{2}}{r^{2}}$

$F=G \frac{m_{1} \: m_{2}}{r^{2}}$

Where $G$ is Newton's gravitaional constant and its experimental value $6.67\times 10^{-11} \frac{N-m^{2}}{kg^{2}}$

Properties of Newton's law for Gravitational force →

There are the following properties of Newton's law for gravitational force

Gravitational force is always an attractive force.

Gravitational force is action and reaction pair and follows Newton's third law.

A Gravitational force is a conservative force.

Gravitational force is central force i.e. it is always acting along the line joining between two particles.

Unit and Dimensional formula of $G$

The unit of $G$ is $\frac{N-m^{2}}{kg^{2}}$

The dimensional Formula of $G$ is $[M^{-1}L^{3}T^{-2}]$

Read More