Spectrum of Hydrogen Atom

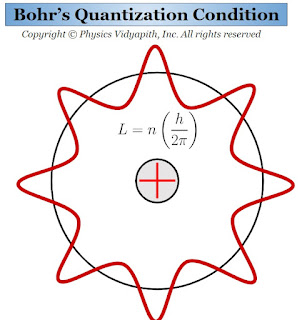
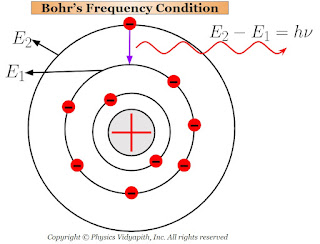
Description: The different series of hydrogen spectra can be explained by Bohr's theory. According to Bohr's theory, If the ionized state of a hydrogen atom be taken zero energy level, then energies of different energy levels of the atom can be expressed by following the formula

$E_{n}=\frac{Rhc}{n^{2}} \qquad (1)$

Where
$R \rightarrow$ Rydberg's Constant
$h \rightarrow$ Planck's Constant
$n \rightarrow$ Quantum Number

According to Plank's Theory

$E_{2} - E_{1} =h \nu \qquad(2)$

So from equation $(1)$

$E_{1}=\frac{Rhc}{n^{2}_{1}} $ and $E_{2}=\frac{Rhc}{n^{2}_{2}} \qquad (3)$

From equation $(2)$ and equation $(3)$

$\frac{Rhc}{n^{2}_{2}} - \frac{Rhc}{n^{2}_{1}} =h \nu $

$\frac{Rhc}{n^{2}_{2}} - \frac{Rhc}{n^{2}_{1}} = \frac{hc}{\lambda} $

$\frac{1}{\lambda}=R \left(\frac{1}{n^{2}_{1}} -\frac{1}{n^{2}_{2}} \right)$

The quantity $\frac{1}{\lambda}$ is called the 'wave number', All the series found in the hydrogen spectrum are explained by the above equation :

(i) Lyman Series: When an atom comes down from some higher energy level (i.e. $n_{2} = 2, 3, 4, ...$) to the first energy level (lowest energy level), (i.e. $n_{1}= 1$), then spectral lines are emitted in the spectrum region of ultraviolet. The equation for obtaining the wavelengths of these spectral lines:

$\frac{1}{\lambda}=R \left(\frac{1}{1^{2}} -\frac{1}{n^{2}_{2}} \right)$

Where $n_{2} = 2, 3, 4, ...$

In 1916, Lyman photographed the lines of this series of hydrogen spectra. Hence, this series is named Lyman series'. The longest wavelength of this series (for $n_{2} = 2$) is $1216 A^{\circ}$ and the shortest wavelength (for $n_{2} = \infty$) is $912 A^{\circ}$. The wavelength $912 A^{\circ}$ corresponding to $n = \infty$ is called the 'series limit'.

(ii) Balmer Series: When an atom comes down from some higher energy level (i.e. $n_{2} = 3, 4, 5, ...$) to the second energy level (i.e. $n_{1}= 2$), then the spectral lines are emitted in the spectrum region of the visible part.

$\frac{1}{\lambda}=R \left(\frac{1}{2^{2}} -\frac{1}{n^{2}_{2}} \right)$

where $n_{2} = 3, 4, 5, ...$

In 1885, Balmer saw and studied first time these spectral lines. The longest wavelength of this series (for $n_{2} = 3$) is $6563 Å$ and the shortest wavelength (for $n_{2} = \infty$) is 3646 Ä.

(iii) Paschen Series: When an atom comes down from some higher energy level (i.e. $n_{2} = 3, 4, 5, ...$) to the third energy level (i.e. $n_{1}= 3$) then the spectral lines are emitted in the spectrum region of infrared.

$\frac{1}{\lambda}=R \left(\frac{1}{3^{2}} -\frac{1}{n^{2}_{2}} \right)$

where $n_{2} = 4, 5, 6, ...$

(iv) Brackett Series: When an atom comes down from some higher energy level (i.e. $n_{2} = 5, 6, 7, ...$) to the fourth energy level (i.e. $n_{1}= 4$), then the spectral lines are also emitted in the spectrum region of infrared.

$\frac{1}{\lambda}=R \left(\frac{1}{4^{2}} -\frac{1}{n^{2}_{2}} \right)$

where $n_{2} = 5,6, 7,.....$

(iv) Pfund Series: When an atom comes down from some higher energy level (i.e. $n_{2} = 6, 7, 8, ...$) to the fifth energy level (i.e. $n_{1}= 5$) then the spectral lines are also emitted in the spectrum region of infrared.

$\frac{1}{\lambda}=R \left(\frac{1}{5^{2}} -\frac{1}{n^{2}_{2}} \right)$

where $n_{2}= 6,7, 8, ....$

Read More

Limitations of Bohr's Model

Although Bohr's model of hydrogen atom and hyarogen like atom was successful in explaining the stability and spectrum even then it has few limitations. which are as follows:

(1) This model could not explain the spectrum of atom having more than one electron.

(2) This model could not explain the relative intensity of spectral lines. (i. e., few transitions are more acceptable than others why?)

(3) When a spectral line is observed by spectroscope of high resolution power, more than one lines are observed. This is known as fine structure of spectral line. Bohr model could not explain this.

(4) Splitting of spectral lines in external magnetic field (Zeeman's effect) and in external electric field (Stark's effect) could not be explained by this model.

(5) This model could not explain the distribution of electrons in different orbit.

Few limitations of Bohr's model are removed in Somer-field's model of atom. (In this model, the orbit of electron was considered as elliptical instead of circular ). But this model also has its limitations. Vector atomic model, which is based on quantum mechanics, explains clearly the structure of atom.

Read More

Bohr's Theory of Hydrogen-Like Atoms

A hydrogen-like atom consists of a very small positively-charged nucleus and an electron revolving in a stable circular orbit around the nucleus.

The radius of electrons in stationary orbits:

Let the charge, mass, velocity of the electron and the radius of the orbit is respectively  $e$, $m$, and $v$  and $r$. The $+ze$ is the positive charge on the nucleus where $Z$ is the atomic number of the atom. As We know that when an electron revolves around the nucleus then the centripetal force on an electron is provided by the electrostatic force of attraction between the nucleus and an electron, we have

$\frac{mv^{2}}{r}=\frac{1}{4 \pi \epsilon_{\circ}} \frac{(Ze)(e)}{r^{2}}$

$mv^{2}=\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} \qquad(1)$

According to the first postulate of Bohr's model of the atom, the angular momentum of the electron is

$mvr=n \frac{h}{2 \pi} \qquad(2)$

Where $n \: (=1,2,3,.....)$ is quantum number.

Now squaring equation $(2)$ and dividing by equation $(1)$, we get

$r=n^{2} \frac{h^{2} \epsilon_{\circ}}{\pi m Z e^{2}} \qquad(3)$

The above equation is for the radii of the permitted orbits. From the above equation, this concluded that

$r \propto n^{2}$

Since, $n =1,2,3,.....$ it follows that the radii of the permitted orbits increased in the ratio $1:4:9:16:,.....$ from the first orbit.

Bohr's Radius:

For Hydrogen Atom $(z=1)$, The radius of the atom of the first orbit $(n=1)$ will be

$r_{1}= \frac{h^{2} \epsilon_{\circ}}{\pi m e^{2}}$

This is called Bohr's radius and its value is $0.53 A^{\circ}$. Since $r \propto n^{2}$, the radius of the second orbit of the hydrogen atom will be $( 4 \times 0.53 A^{\circ}) $ and that of the third orbit $9 \times 0.53 A^{\circ}$

The velocity of electrons in stationary orbits:

The velocity of the electron in permitted orbits can be obtained by the formula of equation $(2)$

$v=n\frac{h}{2 \pi m r}$

Now put the value of $r$ in above eqaution from equation $(3)$, we get

$v=\frac{Ze^{2}}{2 h \epsilon_{\circ}} \left( \frac{1}{n} \right) \quad(4)$

Thus $v \propto \frac{1}{n}$

This shows that the velocity of the electron is maximum in the lowest orbit $n=1$ and as goes on higher orbits velocity decreases.

For Hydrogen Atom $(z=1)$, The velocity of electron to move in the first orbit $(n=1)$ is

$v_{1}=\frac{e^{2}}{2h\epsilon_{\circ}}$

Its value is $2.19 \times 10^{6} m/sec$

Note:

$\frac{v_{1}}{c}= \frac{2.19 \times 10^{6}}{3 \times 10^{8}} =\frac{1}{137}$

Thus, $\frac{v_{1}}{c}$ or $\frac{e^{2}}{2h\epsilon_{\circ}}$ is a pure number. It is called the "Fine Structure Constant" and is denoted by $\alpha$

The energy of electrons in stationary orbits:

The total energy $E$ of a moving electron in an orbit is the sum of kinetic energies and potential energies. The kinetic energy of moving the electron in a stationary orbit is:

$K=\frac{1}{2} m v^{2}$

Now susbtitute the value of $v$ from equation $(1)$, we get

$K=\frac{ze^{2}}{8 \pi \epsilon_{\circ} r}$

The potential energy of a moving electron in an orbit of radius $r$ due to the electrostatic attraction between nucleus and electron is given by

$U=\frac{1}{4 \pi \epsilon_{\circ}} \frac{(Ze)(-e)}{r}$

$U=-\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} $

The total energy of the electron is

$E=K+U$

$E=\frac{ze^{2}}{8 \pi \epsilon_{\circ} r} -\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} $

$E=-\frac{ze^{2}}{8 \pi \epsilon_{\circ} r}$

Subtituting the value of $r$ in above equation from equation $(3)$, we get

$E=-\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{2}} \left( \frac{1}{n^{2}} \right) \qquad(5)$

This is the equation for the energy of the electron in the $n^{th}$ orbit.

Suppose, Excited state energy is $E_{2}$ and lower state energy is $E_{1}$. So the energy difference between these two states is:

$E_{2}- E_{1}= \frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{2}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}} \right) \qquad(6)$

According to the third postulate of Bohr's Atomic model, the frequency $\nu$ of the emitted electromagnetic wave:

$\nu=\frac{E_{2}- E_{1}}{h}$

$\nu=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right)$

The corresponding wavelength $\lambda$ of the emitted electromagnetic radiation is given by

$\frac{c}{\lambda}=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right)$

$\frac{1}{\lambda}=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(7)$

Where $\frac{1}{\lambda}$ is called "wave number" (i.e. number of waves per unit length). In the last equation$(7)$, the quantity $\frac{m e^{4}}{8 \epsilon^{2}_{\circ} c h^{3}}$ is a constant an it is known as "Rydberg Constant (R)". That is

$R = \frac{me^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} \qquad(8)$

So equation $(7)$ can be written as

$\frac{1}{\lambda}=z^{2} R \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(9)$

This is Bohr's formula for hydrogen and hydrogen-like atoms $(He^{+}, Li^{++},.......)$.

For hydrogen $Z=1$

$\frac{1}{\lambda}= R \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(10)$

The value of the Rydberg Constant is

$R = \frac{me^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} = 1.090 \times 10^{7} m^{-1}$

This value fairly agrees with empirical value $(1.097 \times 10^{7} m^{-1})$ obtained experimentally by Balmer.

The total energy in terms of Rydberg's Constant:

The $E$ expression can be written in terms of Rydberg's constant $R$ in a simplified form. So from equation $(5)$ and $(8)$ we get

$E=-Z^{2}\frac{Rhc}{n^{2}} \qquad(11)$

Putting the known values of $R$, $h$ and $c$ taking $1 eV =1.6 \times 10^{-19} \: J$ then we get

$E=-Z^{2}\frac{13.6}{n^{2}} \: eV \qquad(12)$

For a Hydrogen atom, $Z=1$

$E=-\frac{13.6}{n^{2}} \: eV \qquad(12)$

Read More

Bohr's Model of Atom

Bohr's Atomic Model Postulates:

Prof Neil in 1913 Bohr solve the difficulties of Ernest Rutherford's atomic model by applying Planck's quantum theory, For this, he proposed the following three Postulates:

1.) Electrons can revolve only in those orbits in which their angular momentum is an integral multiple of $\frac{h}{2 \pi}$. These orbits have discrete energy and definite radii. So it is called the "stable orbits". If the mass of the electron is $m$ and it is revolving with velocity $v$ in an orbit of radius $r$, then its angular momentum will be $mvr$. According to Bohr's postulate,

$mvr=\frac{nh}{2\pi}$

Where $h$ is Planck's universal constant

This Bohr's equation is called the "Bohr's quantization Condition"

2.) When the electrons revolve in stable orbits then they do not radiate the energy in spite of their acceleration toward the center of the orbit. Hence atom remains stable and is said to exist in a stationary state.

3.) When the atoms receive energy from outside, then one (or more) of their outer electrons leaves their orbit and goes to some higher orbit. These states of the atoms are called the "excited states".

The electrons in the higher orbit stay only for $10^{-8} \: sec$ and return back to anyone lower orbit. While returning back of electrons to lower orbits, they radiate energy in the form of electromagnetic waves.

This radiated energy can be calculated by the energy difference of the electron between the two orbits (i.e. one is higher orbit and the other is lower orbit). If the energy of electron in the higher orbit is $E_{2}$ and that in the lower orbit is $E_{1}$ then net energy difference between the orbits:

$E=E_{2} - E_{1}$

$h \nu=E_{2} - E_{1} \qquad \left( \because E=h\nu \right)$

$\nu=\frac{E_{2} - E_{1}}{h}$

This Bohr's equation is called the "Bohr's frequency condition".

Read More