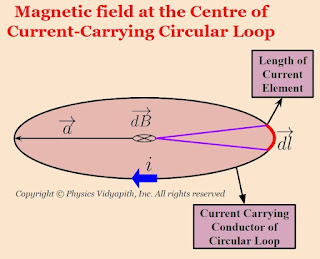
Magnetic field at the center of circular loop

Mathematical Analysis of magnetic field at the center of circular loop:

Let us consider, a current-carrying circular loop of radius $a$ in which $i$ current is flowing. Now take a small length of a current element $dl$ so magnetic field at the center of a circular loop due to the length of current element $dl$. According to Biot-Savart Law:

$dB=\frac{\mu_{\circ}}{4 \pi} \frac{i .dl .sin\: \theta}{a^{2}} $

Here $\theta$ is the angle between length of current element $\left( \overrightarrow{dl} \right)$ and radius $\left( \overrightarrow{a} \right)$. These are perpendicular to each other i.e. $\theta = 90^{\circ}$

$dB=\frac{\mu_{\circ}}{4 \pi} \frac{i .dl .sin\: 90^{\circ}}{a^{2}} $

$dB=\frac{\mu_{\circ}}{4 \pi} \frac{i .dl }{a^{2}} \qquad \left(1 \right)$

The magnetic field at the center due to a complete circular loop

$B=\int dB \qquad \left(2 \right)$

From equation $(1)$ and equation $(2)$

$B=\int \frac{\mu_{\circ}}{4 \pi} \frac{i .dl}{a^{2}}$

$B=\frac{\mu_{\circ}}{4 \pi} \frac{i}{a^{2}} \int dl $

For complete loop $\int dl = 2 \pi a$, So from above equation that can be written as

$B=\frac{\mu_{\circ}}{4 \pi} \frac{i}{a^{2}} \left( 2 \pi a \right) $

$B=\frac{\mu_{\circ} i}{2 a}$

This is an equation of the magnetic field at the center of the circular loop.