Davisson and Germer's Experiment and Verification of the de-Broglie Relation

Davisson and Germer's Experiment on Electron Diffraction:

Davisson and Germer's experiment verifies the wave nature of electrons with the help of diffraction of the electron beam as wave nature exhibits the diffraction phenomenon.

Principle: The principle of Davisson and Germer's experiment is based on the diffraction phenomenon of the electron beam by crystal and it verifies the de-Broglie relation.

Theoretical Formula: If a narrow beam of electrons is accelerated by a potential difference $V$ volts, the kinetic energy $K$ acquired by each electron in the beam is given by

$K=eV \qquad(1)$

Where $e$ is the charge of an electron

The de-Broglie wavelength is given by

$\lambda = \frac{h}{\sqrt {2m_{\circ} K \left( 1+ \frac{E_{K}}{2m_{\circ}c^{2}} \right)}}$

If $E_{K} \lt \lt 2m_{\circ}c^{2}$, then the term $\frac{E_{K}}{2m_{\circ}c^{2}}$ will be negligible. So above equation can be written as

$\lambda = \frac{h}{\sqrt {2m_{\circ} K}} \qquad(2)$

Now subtitute the value of $K$ from equation $(1)$ to equation $(2)$ then equation $(2)$ can be written as

$\lambda = \frac{h}{\sqrt {2m_{\circ} eV}}$

Now substitute the numerical value of $h$, $m_{\circ}$ and $e$, we get

$\lambda = \frac{6.63 \times 10^{-34}}{2 \times 9.11 \times 10^{-31} \times 1.6 \times 10^{-19} \times V}$

$\lambda = \frac{6.63 \times 10^{-9}}{29.15\times V}$

$\lambda = \frac{12.28}{\sqrt{V}}A^{\circ} \qquad(3)$

This is the theoretical value of $\lambda$ for the known potential difference in volts.

The calculation shows that the wavelength of the waves associated with the beam of electrons is of the same order as that of X-rays. Therefore, if such a beam of electrons is reflected from a crystal, the reflected beam will show the same diffraction and interference phenomena as for X-rays of the same wavelength. This consideration was the basis of Davisson and Germer's experiments. In one set of experiments, the [111] face of the nickel crystal was arranged perpendicular to the incident beam of electrons.

Apparatus:

There are the following apparatus is used in the Davisson and Germer experiment.

1. Electron gun
2. Target
3. Electron detector or Faraday's cylinder
4. Galvanometer

1. Electron gun: The electron gun is a device that is used to produce a highly accelerated and collimated electron beam by applying high potential.

2. Target: It is a single large metal crystal i.e. nickel used as a target. In crystal, the atoms are arranged in regular lattice i.e. [111] so that the surface lattice of the crystal acts as a diffraction grating and the electrons get diffracted by the crystal in different directions. The electron beam is incident normal to the nickel crystal. The crystal can be rotated about an axis perpendicular to the incident beam so that various azimuthal angles could be used.

3. Electron detector or Faraday's cylinder: It is used to detect or measure the intensity of diffracted beams of electrons. It can be moved along a circular scale $S$. This electron detector is connected to a Galvanometer.

4. Galvanometer: The galvanometer is a device that is used to measure the very small amount of current following in the circuit.

The whole apparatus is completely enclosed and highly evacuated.

Working: When a low potential is applied to the electron gun so that a beam of slow electrons emerges from the gun and falls normally on the surface of the crystal. To collect the diffracted electrons, the Faraday cylinder is moved to various positions on the scale $S$ and the corresponding galvanometer measures the current at each position through an electron detector. The observation is repeated for electrons accelerated through different potentials. The current which is a measure of the intensity of the diffracted electron beam, is plotted against the diffracting angle $\phi$ for each accelerating potential as shown in the figure below

It is observed in the curves that at the voltage of $40$ volts, a smooth curve is obtained and a bump begins to appear in the curve for $44$ volts. As the potential difference is further increased, the bump starts shifting upward and becomes most prominent in the curve for $54$ volts at $\phi = 50 ^{\circ}$. Beyond $54$ volts the bump gradually diminishes and becomes insignificant at $68$ volts. The pronounced current peak at $54$ volts and at $50^{\circ}$ provided an evidence that electrons were diffracted by the target and verifies the existence of electron wave nature.

Calculation of Wavelength:

Theoretical Calculation:

The wavelength of electron at $54$ volts can be find by de- Broglie formula as shown in the equation $(3)$

$\lambda= \frac{12.28}{\sqrt{54}}\: A^{\circ}$

$\lambda= 1.671 \: A^{\circ} $

Experimental Calculation:

Experimental calculation is done by Bragg's diffraction equation

$n \lambda = 2d \: sin\theta$

Where
$d \rightarrow$ interplanar Spacing
$n \rightarrow$ Order of plane

For nickel crystal :
$n=1$
$d=0.91 A^{\circ}$

In the experiment, the diffracted electron beam appearing at $\phi=50 ^{\circ}$ aries from wave-like diffraction from the family of Bragg's planes.
The corresponding angle of incidence relative to the family of Bragg's planes is
$\theta = \frac{180 - \phi}{2}$
$\theta = \frac{180 - 50}{2}$
$\theta= 65^{\circ}$

Now apply these values to Bragg's equation as written above

$\lambda = 2 \times 0.91 \times sin 65^{\circ} $

$\lambda = 2 \times 0.91 \times 0.906 $

$\lambda = 1.65 A^{\circ} $

The theoretical and experimental value at $54$ volts verifies the wave nature of electrons by diffraction of the beam.

Read More

Minimum Energy Or Zero Point Energy of a Particle in an one dimensional potential box or Infinite Well

Zero Point Energy of a Particle in an Infinite Well Potential Well:

The normalized wave function or eigenwave function:

$\psi_{n}(x) = \sqrt{\frac{2}{L}} sin \left( \frac{n\pi x}{L} \right)$

The probability density

$| \psi_{n}(x)|^{2} = \frac{2}{L} sin^{2} \left( \frac{n\pi x}{L} \right)$

The energy of a particle in a one-dimensional box or infinite potential well:

$E_{n}=\frac{n^{2}h^{2}}{8 mL^{2}}$

Where $n$ is called the quantum number and $n=1,2,3,4..........$ For $n=0, \psi_{n}(x)=0$ and $| \psi_{n}(x)|^{2}=0$. This shows that for $n=0$ $| \psi_{n}(x)|^{2}=0$ will be zero everywhere in the box which means that the probability of finding the particle inside the box is zero. i.e. particle is not present at all inside the box. Thus $n=0$ is not possible.

If $n\neq 0$ then $E \neq 0$. This means that the minimum energy of the particle in the box will not be zero. The minimum energy value will be obtained for the next lowest value of $n$ i.e. for $n=1$, which is

$E_{1}=\frac{h^{2}}{8 mL^{2}}$

This minimum energy of the particle is often called zero point energy which is finite inside the box. According to classical mechanics, the minimum value $E=0$ is also permissible.

Read More

Bohr's Quantization Condition

The Quantization Condition in Bohr Theory of Hydrogen Atom:

$L=\frac{nh}{2 \pi}$

For the angular momentum L, the electron moves arbitrarily only in a stationary circular orbit. According to De Broglie's hypothesis, this condition can be easily obtained. For this purpose, there are following assumptions given below:

1.) The motion of the electron in a stationary circular orbit is represented by a standing matter-wave. If the wavelength of the wave is $\lambda$ then the De Broglie relation

$\lambda=\frac{h}{mv} \qquad(1)$

Where
$m \rightarrow$ The mass of the electron and
$v \rightarrow$ The Velocity in the orbit.

2.) The circular orbit contains an integral number of wavelengths, i.e.

$2 \pi r_{n}= n \lambda $

$\frac{2 \pi r_{n}}{\lambda}= n \qquad(2)$

Where $n=1,2,3............$ and $r_{n}$ is the radius of the orbit.

Substituting the value of $\lambda$ in equation$(2)$

$\frac{2 \pi r_{n} m v}{h} =n$

$mvr_{n} =\frac{nh}{2\pi}$

$L=\frac{nh}{2\pi}$

Which is Bohr's quantization condition.

Read More

Drawbacks of Old Quantum Theory

Planck's quantum hypothesis with its application and extension to explain the black body radiation like the photo-electric effect, the Compton effect, the variation of specific heat of solid with temperature and the spectrum of hydrogen is now called the Old quantum theory. Through these phenomena are successfully explained by the theory, there are numerous drawbacks of the theory. A few of them are as follows.

1.) Bohr's quantization rules are arbitrary. The theory does not provide a physical explanation for the assumptions.

2.) The old quantum theory cannot be applied to explain the spectra of helium and of more complex atoms.

3.) It can provide only a qualitative and incomplete explanation of the intensities of the spectral lines.

4.) It can not explain the dispersion of light.

5.) The theory of non-harmonic vibrations of systems cannot be applied to explain the vibrations of systems.

Read More

One dimensional Step Potential Barrier for a Particle

Potential Step:

1.) In region $(I)$  i.e.$(-\infty \leq \: x \lt \: 0)$
2.) In region $(II)$ i.e. $(0 \leq \:x \: \leq +\infty)$
Case $(1)$	When $E \lt V_{\circ}$
A.) Expression for the Amplitudes $B$ and $C$ in terms of the Amplitude $A$ B.) Expression for the wave function in the region $(I)$ and $(II)$ C.) Expression for the Probability Current Densities D.) Reflection and Transmission Coefficients
Case $(2)$ :	When $E \gt V_{\circ}$
A.) Expression for the Amplitudes $B$ and $C$ in terms of the Amplitude $A$ B.) Expression for the wave function in the region $(I)$ and $(II)$ C.) Expression for the Probability Current Densities D.) Reflection and Transmission Coefficients

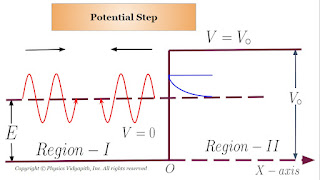
One dimensional step potential barrier for a particle is shown in the figure below.

The meaning of the figure is that the region $(I)$ is at left hand side of the origin $O$ and the potential energy of a particle is zero in this region $(I)$. The region $(II)$ is at the right hand side of $O$ and this region $II$ has constant potential equal to $V_{\circ}$. Such a potential barrier does not exist in nature, but it is approximately similar to the instantaneous potential difference between the dees of a cyclotron or the surface potential barrier of a metal.

Suppose a uniform beam of particles each of mass $m$ and having kinetic energy $E$ is traveling parallel to the x-axis from left to right in the region $(I)$, and is incident on the potential step. In region $(I)$ the energy $E$ of a particle is whole kinetic energy, and in region $(II)$ it is partly kinetic and partly potential energy.

If $E \lt V_{\circ}$, then according to classical mechanics, a particle can enter in the region $(II)$. However according to quantum mechanics although the wave function for an incident particle has a finite value in the region $(II)$ there is no steady transmission of the particle has finite value in this region $(II)$, all the particles are reflected back from the potential step $V_{\circ} \gt E$. In the following discussion, we investigate this behavior of the particles.

Let $\psi_{1}(x)$ and $\psi_{2}(x)$ be the wave function for the motion of a particle in the beam in the region $(I)$ and $(II)$ respectively.

1.) In region $(I)$ i.e. $(-\infty \leq \: x \lt \: 0)$:

According to the time-independent Schrodinger wave equation is:

$-\frac{\hbar^{2}}{2m} \frac{d^{2} \psi_{1}}{dx^{2}}=E \psi_{1}$

$\frac{d^{2} \psi_{1}}{dx^{2}} + \frac{2mE}{\hbar^{2}} \psi_{1} =0$

Let $k_{1}^{2}=\frac{2mE}{\hbar^{2}} $, Now substitute this value in the above equation that can be written as

$\frac{d^{2} \psi_{1}}{dx^{2}} + k_{1}^{2} \psi_{1} =0 \qquad(1)$

2.) In region $(II)$ i.e. $(0 \leq \:x \: \leq +\infty)$:

Case $(1)$ : When $E \lt V_{\circ}$

Then according to the time-independent Schrodinger wave equation for the above case is:

$\frac{d^{2} \psi_{2}}{dx^{2}} + \frac{2m \left(E-V_{\circ} \right)}{\hbar^{2}} \psi_{2} =0$

$\frac{d^{2} \psi_{2}}{dx^{2}} - \frac{2m \left(V_{\circ} -E \right)}{\hbar^{2}} \psi_{2} =0$

Let $\beta^{2}=\frac{2m\left(V_{\circ} -E \right)}{\hbar^{2}} $, Now substitute this value in the above equation that can be written as

$\frac{d^{2} \psi_{2}}{dx^{2}} - \beta^{2} \psi_{2} =0 \qquad(2)$

The general solution of the equation $(1)$ and equation $(2)$ is

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad(3)$

$\psi_{2} (x) = C e^{- \beta \: x} + D e^{\beta \: x} \qquad(4)$

In equation $(3)$ the term $A e^{ik_{1}x}$ represents a wave of amplitude $A$ traveling in the positive x-axis direction and term $B e^{-ik_{1}x} $ is the wave of amplitude $B$ reflected from potential step in the negative x-axis direction. In equation $(4)$ the term $C e^{- \beta \: x}$ is an exponentially decreasing wave function representing a non-oscillatory disturbance that penetrates the potential barrier for some finite distance in the positive x-axis direction and the term $D e^{\beta \: x}$ is an exponentially increasing wave function in the positive x-axis direction. According to the physical interpretation, wave function $\psi$ must remain finite when $x$ approaches $\infty$. From this condition, it follows that $D=0$. Hence in the region $(II)$, the valid solution of the wave equation is:

$\psi_{2} (x) = C e^{- \beta \: x} \qquad(5)$

A.) Expression for the Amplitudes $B$ and $C$ in terms of the Amplitude $A$:

i) At $x=0$, we have

$\psi_{1}(0) = \psi_{2}(0)$

So from equation $(3)$ and equation $(5)$, we have

$A+B=C \qquad(6)$

ii) We also have

$\left( \frac{d\psi_{1}}{dx} \right)_{x=0} = \left( \frac{d\psi_{2}}{dx} \right)_{x=0}$

So again from equation $(3)$ and equation $(5)$, we have

$A\:i\:k_{1} - B\:i\:k_{1} = - C \: \beta$

$A - B = - \frac{C \: \beta}{i\:k_{1} }$

$A - B = \frac{iC \: \beta}{k_{1} } \qquad(7)$

Adding equation $(6)$ and equation $(7)$

$2A = \left( 1 + \frac{ i \beta}{k_{1}} \right)C$

$2A = \left(\frac{k_{1} + i \beta}{k_{1}} \right)C$

$C = \left(\frac{2k_{1} }{k_{1} + i \beta} \right)A \qquad(8)$

Now subtracting the equation $(7)$ from equation $(6)$

$2B = \left( 1 - \frac{ i \beta}{k_{1}} \right)C$

$2B = \left(\frac{k_{1} - i \beta}{k_{1}} \right)C$

Now substitute the value of $C$ from equation $(8)$ in the above equation then we get

$2B = \left(\frac{k_{1} - i \beta}{k_{1}} \right) \left(\frac{2k_{1} }{k_{1} + i \beta} \right)A$

$B = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} \right)A \qquad(9)$

The equation $(8)$ and equation $(9)$ can be expressed in polar form.

Let $k_{1}= r \: cos\delta$ and $\beta=r\: sin \delta$

Then $r=\sqrt {k_{1}^{2} + \beta^{2}}$ and $tan \delta =\frac{\beta}{k_{1}}$

Now subtitute the value of $k_{1}$ and $\beta$ in equation $(9)$

Now substitute the value of $k_{1}$ and $\beta$ in equation $(9)$

$B = \left(\frac{r \: cos\delta - i r\: sin \delta}{r \: cos\delta + i r\: sin \delta} \right)A $

$B = \left(\frac{ \: cos\delta - i \: sin \delta}{ \: cos\delta + i \: sin \delta} \right)A $

$B = \left(\frac{ e^{-i\delta}}{ e^{i\delta}} \right)A $

$B = e^{-2i \delta} A \qquad(10) $

Now from eqaution $(8)$

$C = \left(\frac{2k_{1} }{k_{1} + i \beta} - 1 + 1 \right)A $

$C = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} +1 \right)A $

Now substitute the value of $k_{1}$ and $\beta$ in equation $(8)$

$C = \left(\frac{r \: cos\delta - i r\: sin \delta}{r \: cos\delta + i r\: sin \delta} +1 \right)A $

$C = \left(\frac{ \: cos\delta - i \: sin \delta}{ \: cos\delta + i \: sin \delta} +1 \right)A $

$C = \left(e^{-2i \delta} +1 \right)A \qquad(11)$

B.) Expression for the wave function in the region $(I)$ and $(II)$:

(i.) In region $(I)$: $x \lt 0$:

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ from \: eqaution \: (3) \right\}$

Now substitute the value of $B$ in the above equation:

$\psi_{1} (x) = A e^{ik_{1}x} + e^{-2i \delta} A e^{-ik_{1}x} $

$\psi_{1} (x) = A e^{-i \delta} \left( e^{ik_{1}x} e^{i \delta} + e^{-i \delta} A e^{-ik_{1}x} \right) $

$\psi_{1} (x) = 2A e^{-i \delta} \left[ \frac{e^{ik_{1}x} e^{i \delta} + e^{-i \delta} A e^{-ik_{1}x}}{2} \right] $

$\psi_{1} (x) = 2A e^{-i \delta} cos \left(k_{1}x + \delta \right) \qquad(12) $

(ii.) In region $(II)$: $x \gt 0$:

$\psi_{2} (x) = C e^{- \beta \: x} \qquad \left\{ from \: eqaution \: (5) \right\}$

Now substitute the value of $C$ in the above equation:

$\psi_{2} (x) = \left(e^{-2i \delta} +1 \right)A e^{- \beta \: x} $

$\psi_{2} (x) = A e^{-i \delta} \left(e^{-i \delta} +e^{i \delta} \right) e^{- \beta \: x} $

$\psi_{2} (x) = 2A e^{-i \delta} \left( \frac{e^{-i \delta} +e^{i \delta}}{2} \right) e^{- \beta \: x} $

$\psi_{2} (x) = 2A e^{-i \delta} \left( \frac{e^{-i \delta} +e^{i \delta}}{2} \right) e^{- \beta \: x} $

$\psi_{2} (x) = \left( 2A e^{-i \delta} cos \delta \right) e^{- \beta \: x} \qquad(13)$

This shows that the wave function in the region $(II)$ is exponentially damped.

C.) Expression for the Probability Current Densities:

(i.) In region $(I)$:

a.) The probabilty current density $S_{1}$ for the incident beam of particle is given by

$S_{i} =(Incident \: wave \: function)(Complex \: conjugate \: of \: incident \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{i} =(A e^{ik_{1}x})(A e^{ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} e^{ik_{1}x} e^{-ik_{1}x} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} \frac{\hbar k_{1}}{m}$

$S_{i} = | A|^{2} \frac{\hbar k_{1}}{m} \qquad(14)$

b.) The probability current density $S_{r}$ for the reflected beam of particles is given by:

$S_{r} =(Reflected \: wave \: function)(Complex \: conjugate \: of \: reflected \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{r} =(B e^{-ik_{1}x})(B e^{-ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{r} = | B |^{2} \frac{\hbar k_{1}}{m} \qquad(15)$

Hence the net probability current density in the region $(I)$ is given by

$S=S_{i} - S_{r}$

$S=\frac{\hbar k_{1}}{m} \left(| A |^{2} - | B |^{2} \right) \qquad(16)$

The intensity of waves:

We know that

$B = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} \right)A \qquad \left\{ From \: equation \: (9) \right\}$

The complex conjugate of this equation is:

$B^{*} = \left(\frac{k_{1} + i \beta}{k_{1} - i \beta} \right)A^{*} $

$BB^{*}=AA^{*}$

$ | B^{2} | = | A^{2}| \qquad(17)$

Hence the net probability current in the region $(I)$ to the left of the region $O$ is zero.

The equation $ | B^{2} | = | A^{2}|$ shows that the intensity of the reflected wave is equal to that of the incident wave, or the number of particles per second passing normally through the unit area of the incident beam is equal to the number of particles per second passing normally through unit area of the reflected beam. Consequently, the incident and reflected probability currents cancel one another.

(ii.) In region $(II)$:

From the relation $ | B^{2} | = | A^{2}|$ we infer that the probability current density in the region $(II)$ to the right of the origin should be zero. However, we can prove this conclusion using the wave function

$\psi_{2}= C e^{-\beta x}$

and its complex conjugate

$\psi^{*}_{2}= C^{*} e^{-\beta x}$

The proof is as follows:

The probability current density in the region $(II)$ for the transmitted beam of the particles is given by

$S_{t}= -\frac{i \hbar}{2m} \left[ \psi^{*}_{2} \frac{\partial \psi_{2}}{\partial x} - \psi_{2} \frac{\partial \psi^{*}_{2}}{\partial x} \right]$

Now Substitute the value of $\psi$ and $\psi^{*}$ in this above equation:

$S_{t}= -\frac{i \hbar}{2m} \left[C^{*} e^{-\beta x} \frac{\partial C e^{-\beta x}}{\partial x} - C e^{-\beta x} \frac{\partial C^{*} e^{-\beta x}}{\partial x} \right]$

$S_{t}= -\frac{i \hbar}{2m} \left[CC^{*} e^{-\beta x} \frac{\partial e^{-\beta x}}{\partial x} - CC^{*} e^{-\beta x} \frac{\partial e^{-\beta x}}{\partial x} \right]$

$S_{t}= -\frac{i \hbar}{2m} \left[CC^{*} e^{-\beta x} (-\beta) e^{-\beta x} - CC^{*} e^{-\beta x} (-\beta) e^{-\beta x} \right]$

$S_{t}= -\frac{i \hbar}{2m} \left[-CC^{*} e^{-2\beta x} (\beta) + CC^{*} e^{-2\beta x} (\beta) \right]$

$S_{t}=0 \qquad(18)$

The probability current density $S_{t}$ for a transmitted beam of particles is zero

D.) Reflection and Transmission Coefficients:

(i.)Reflection Coefficients:

The reflection coefficient $R$ is defined as the ratio of the probability current density $S_{r}$ for the reflected beam of particles to the probability current density $S_{i}$ for the incident beam of particles. Thus it is given by

$R=\frac{S_{r}}{S_{i}}$

$R=\frac{| B |^{2} \frac{\hbar k_{1}}{m}}{ | A |^{2} \frac{\hbar k_{1}}{m} }$

$R=\frac{| B |^{2} }{| A |^{2}} \qquad(19)$

In this case $(V_{\circ} \gt E)$, $ | B^{2} | = | A^{2}|$ Now the above equation $(19)$ can be written as

$R=1 \qquad(20)$

This shows that the reflection of the incident beam, at the potential step is total.

(ii) Transmission Coefficients:

The transmission coefficient $T$ is defined as the ratio of the probability current density $S_{t}$ for the transmitted beam of the particle to the probability current density $S_{i}$ for the incident beam. Thus it is given by

$T=\frac{S_{t}}{S_{i}} \qquad(21)$

In this case: The probability of current densityin region $(II)$ is zero i.e. $S_{t}=0$ then transmission coefficient

$T=0$

So from above equation, we can conclude that the transmission coefficient of the beam of particles is zero.

Conclusions:

From the foregoing discussion, we draw the following inference:

i.) The reflection of the incident beam of particles, at the potential step is total.

ii.) There is no probability of current density anywhere. To the left hand side of the potential step, the incident and the reflected probability of currents density cancel to each other, and to the right ahnd side of the step, probability of currents density is zero.

iii.) To the right of the step the wave function is not zero, but it is exponentially damped. Therefore there is a finite or definite probability of finding the particle in the region $(II)$

If $V_{\circ} \rightarrow \infty$ and $E$ is finite, then

$\beta=\sqrt {\frac{2m \left( V_{\circ} -E \right)}{\hbar^{2}}} \rightarrow \infty $

In this case the wave function in region $(II)$ is $\psi_{2}= C \: e^{-\beta x} \rightarrow 0 $

$B = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} \right)A $, and $C = \left(\frac{2k_{1} }{k_{1} + i \beta} \right)A$

$\underset{\beta \rightarrow \infty}{Lim} \:\: \frac{B}{A}=\frac{\frac{k_{1}}{\beta} - i}{\frac{k_{1}}{\beta}+i} = -1$

$\frac{B}{A} =-1$ Or $A+B=0$ $\qquad(22)$

And, $\underset{\beta \rightarrow \infty}{Lim} \:\: \frac{C}{A}=\frac{2k_{1}} {k_{1}+i \beta} = 0$

$C=0 \qquad(23)$

Or

Hence the wave function

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ From \: equation (3) \right\}$

At $x=0$ is

$\psi_{1} (0) = A + B=0 \qquad(24)$

And the wave function $\psi_{2}= C \: e^{-\beta x}$

At $x=0$ is $\psi_{2}=C=0$

The slope of $\psi_{1}$ at $x=0$ is

$\left( \frac{d\psi_{1}}{dx} \right)_{x=0}= ik_{1} \left( A-B \right) = 2 i k_{1} A \qquad(25)$

Thus at a point where the potential suddenly increases from zero to an infinite value the wave function $\psi_{1}$ becomes zero and ts slope suddenly falls from a finite value $2ik_{1}A$ to zero.

In region $(II)$ : $(0 \leq \:x \: \leq +\infty)$:

Case $(2)$ : When $E \gt V_{\circ}$

If $E \gt V_{\circ}$, then the time-independent Schrodinger wave equation is

$\frac{d^{2} \psi_{2}}{dx^{2}} + \frac{2m \left(E-V_{\circ} \right)}{\hbar^{2}} \psi_{2} =0$

Let $k_{2}^{2}=\frac{2m \left(E-V_{\circ} \right)}{\hbar^{2}}$, Now put this value in the above equation which can be written as

$\frac{d^{2} \psi_{2}}{dx^{2}} - k_{2}^{2} \psi_{2} =0 \qquad(26)$

The general solution of the equation $(26)$ is

$\psi_{2} (x) = G e^{ik_{2}x} + H e^{-ik_{1}x} \qquad(27)$

In this equation the term $G e^{ik_{2}x}$ represents a wave traveling from the potential step in the positive x-direction, and the term $H e^{-ik_{1}x}$ a wave traveling in the negative x-direction towards the potential step. Since the particles are incident only from the left of the potential step $H$ must be zero. Hence in the region, $(II)$ the valid solution of the wave equation is

$\psi_{2} (x) = G e^{ik_{2}x} \qquad(28)$

A.) Expression for the Amplitudes $B$ and $G$ in terms of the Amplitude $A$:

i) At $x=0$, we have

$\psi_{1}(0) = \psi_{2}(0)$

So from equation $(3)$ and equation $(28)$, we have

$A+B=G \qquad(29)$

ii) At this condition that the derivative of the wave function is continuous at $x=0$

$\left( \frac{d\psi_{1}}{dx} \right)_{x=0} = \left( \frac{d\psi_{2}}{dx} \right)_{x=0}$

$A \: ik_{1} - B \: ik_{1} =G \: ik_{2} $

$A-B =\frac{k_{2}}{k_{1}}G \qquad(30)$

Adding equation $(29)$ and equation $(30)$, we get

$2A=\left(\frac{k_{1}+k_{2}}{k_{1}}\right) G$

$G=\left(\frac{2k_{1}}{k_{1} +k_{2}}\right) A \qquad(31)$

Subtracting equation $(30)$ and equation $(29)$, we get

$2B=\left(\frac{k_{1} - k_{2}}{k_{1}}\right) G$

Now subtitute the vaue of $G$ from equation $(31)$ to the above equation

$2B=\left(\frac{k_{1} - k_{2}}{k_{1}}\right) \left(\frac{2k_{1}}{k_{1} +k_{2}}\right) A$

$B=\left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right) A \qquad(32)$

B.) Expression for the wave function in region $(I)$ and $(II)$

(i.) In region $(I)$: $x \lt 0$:

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ from \: eqaution \: (3) \right\}$

$\psi_{1} = A \left[ e^{ik_{1}x} + \left( \frac{k_{1} - k_{2}}{k_{1} +k_{2}} \right) e^{-ik_{1}x} \right] \qquad(33)$

ii.) In region $(II)$: $x \gt 0$:

$\psi_{2} (x) = G e^{ i k_{2} \: x} \qquad \left\{ from \: eqaution \: (28) \right\}$

$\psi_{2} (x) = \left(\frac{2k_{1}}{k_{1} +k_{2}}\right) A e^{ i k_{2} \: x} \qquad (34)$

C.) Expression for the Probability Current Densities:

(i.) In region $(I)$:

a.) The probabilty current density $S_{1}$ for the incident beam of particle is given by

$S_{i} =(Incident \: wave \: function)(Complex \: conjugate \: of \: incident \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{i} =(A e^{ik_{1}x})(A e^{ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} e^{ik_{1}x} e^{-ik_{1}x} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} \frac{\hbar k_{1}}{m}$

$S_{i} = | A |^{2} \frac{\hbar k_{1}}{m} \qquad(35)$

b.) The probability current density $S_{r}$ for the reflected beam of particles is given by:

$S_{r} =(Reflected \: wave \: function)(Complex \: conjugate \: of \: reflected \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{r} =(B e^{-ik_{1}x})(B e^{-ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{r} = | B |^{2} \frac{\hbar k_{1}}{m} \qquad(36)$

Hence the net probability current density in the region $(I)$ is given by

$S=S_{i} - S_{r}$

$S=\frac{\hbar k_{1}}{m} \left(| A |^{2} - | B |^{2} \right) \qquad(37)$

From equation $(32)$

$|B|^{2}=\left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right)^{2} |A|^{2}$

Substitute the above equation value in equation $(37)$

$S=\frac{\hbar k_{1}}{m} \left(| A |^{2} - \left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right)^{2} |A|^{2} \right)$

$S=\frac{\hbar k_{1}}{m} | A |^{2} \left[ 1 - \left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right)^{2} \right]$

$S=\frac{\hbar k_{1}}{m} |A|^{2} \left[ \frac{4 k_{1} k_{2}}{\left(k_{1} +k_{2} \right)^{2}} \right]$

$S=\frac{4 k_{1} k_{2}}{\left(k_{1} +k_{2}\right)^{2}} \left( \frac{\hbar k_{1}}{m} \right) | A |^{2} \qquad(38)$

(ii.) In region $(II)$:

The probability current density $S_{t}$ for the transmitted beam of particles in region $(II)$ is given by

$S_{t}= \left( G e^{ i k_{2} \: x} \right) \left( G e^{ i k_{2} \: x} \right)^{*} \frac{\hbar k_{2}}{m} $

$S_{t}= \frac{\hbar k_{2}}{m} |G|^{2} \qquad(39)$

From equation $(31)$, we have

$|G|^{2}=\left(\frac{2k_{1}}{k_{1} +k_{2}}\right)^{2} |A|^{2}$

So substitute the value of the above equation in equation $(39)$, then we get

$S_{t}= \frac{\hbar k_{2}}{m} \left(\frac{2k_{1}}{k_{1} +k_{2}}\right)^{2} |A|^{2}$

$S_{t}= \frac{4k^{2}_{1}}{\left(k_{1} +k_{2}\right)^{2}} \left( \frac{\hbar k_{2}}{m} \right) |A|^{2} \qquad(40)$

The equation $(38)$ and equation $(40)$ shows that $S=S_{t}$. i.e. The net probability density in the direction from left to right in the region $(I)$ is equal to the probability current density in the region $(II)$.

D.) Reflection and Transmission Coefficients:

(i.)Reflection Coefficients:

The reflection coefficient $R$ is defined as the ratio of the probability current density $S_{r}$ for the reflected beam of particles to the probability current density $S_{i}$ for the incident beam of particles. Thus it is given by

$R=\frac{S_{r}}{S_{i}}$

$R=\frac{| B |^{2} \frac{\hbar k_{1}}{m}}{ | A |^{2} \frac{\hbar k_{1}}{m} }$

$R=\frac{| B |^{2} }{| A |^{2}}$

Now using the equation $(32)$ we get

$R=\frac{\left( k_{1} -k_{2} \right)}{\left( k_{1} + k_{2} \right)} \qquad(41)$

(ii) Transmission Coefficients:

The transmission coefficient $T$ is defined as the ratio of the probability current density $S_{t}$ for the transmitted beam of the particle to the probability current density $S_{i}$ for the incident beam. Thus it is given by

$T=\frac{S_{t}}{S_{i}} $

$T=\frac{| G |^{2} \frac{\hbar k_{2}}{m}}{ | A |^{2} \frac{\hbar k_{1}}{m} }$

$T=\frac{| G |^{2} k_{2}}{ | A |^{2} k_{1} }$

Now using equation $(31)$, we get

$T= \frac{k_{2}}{k_{1}} \left( \frac{2 k_{1}}{k_{1} + k_{2}} \right)^{2}$

$T= \frac{k_{2}}{k_{1}} \frac{4 k^{2}_{1}}{\left( k_{1} + k_{2} \right)^{2}} \qquad(42)$

Adding the equation $(41)$ and equation $(42)$ it is easily verified that

$R+T=1 \qquad(43)$

Read More

Description of Compton Effect : Experiment Setup, Theory, Theoretical Expression, Limitation, Recoil Electron

The Compton Effect

1	Compton Experiment Setup
2	Theory of the Compton Effect
3	Theoretical Derivation of Compton Effect (Equation of Compton Shift)
4	Limitation of Compton Effect
5	Compton Recoil Electron- 5(a)Relation between $\theta$ and $\phi$ 5(b) Kinetic Energy of the Recoil Electron

1.) Compton Experiment Setup:

The Compton effect is used to verify the particle nature of matter by applying the photoelectric effect. The setup of the Compton experiment as shown in the figure below which consists of the following parts

i.) X-ray source

ii.) Collimator

iii.) Target

iv.) Bragg's Spectrometer

i.) X-ray Source: The X-ray source is used to produce the monochromatic X-ray

ii.) Collimators: The collimators consist of slits that are used to pass the photon in the same direction.

iii.) Target: The target is made up of low atomic number material (i.e. Beryllium, Graphite, Aluminium) in which the monochromatic x-ray is incident and scattered in all directions.

iv.) Braggs Spectrometer: The Braggs spectrometer is used to measure the intensity of these scattered photons of monochromatic X-ray at different angles by the analyzing crystal and ionization chamber.

Working:

When the monochromatic X-ray is produced through an X-ray source and this monochromatic X-ray passes through slit $S_{1}$ and $S_{2}$ (i.e. Collimator). This slit $S_{1}$ and $S_{2}$ passes only the photon of a monochromatic X-ray beam in one direction. Now this beam is incident on graphite block (i.e. Target) and scattered in all directions. Now the intensity of the scattered beam at different angles is measured by a Braggs spectrometer. The major measured intensity by the Braggs spectrometer at different angles is shown in the figure below.

2.) Theory of the Compton Effect:

To explain the effect, Compton applied Einstein's quantum theory of light with the assumption that incident photons possess momentum. The postulates on which the theory is based are as follows.

i.) A beam of monochromatic X-ray is consist of a stream of photons having energy $h\nu$ and momentum $\frac{h\nu}{c}$. These photons travel in the direction of the beam with the speed of light.

ii.) The scattering of X-rays by atoms of graphite element is the result of elastic collisions between photons and electrons. This is an elastic collision so the energy and momentum will be conserved (i.e. in such a collision there is no loss of kinetic energy).

Note: The outer shell electron is loosely bound with the atom and required a very small amount of energy to leave the atom but the X-ray photons have very high energy. So the loosely bound electron of the atom leaves atom the permanently. Therefore for the X-ray loosely bound electrons can be considered as free electrons at rest.

3.) Theoretical Derivation of Compton Effect (Equation of Compton Shift):

Let us consider

The energy of the incident photon $E_{i}=h\nu$

The momentum of the incident photon $p_{i}=\frac{h\nu}{c}$

The energy of the scattered photon $E_{s}=h\nu'$

The momentum of the scattered photon $p_{s}=\frac{h\nu'}{c}$

The relativistic energy of the recoil electron $E_{e}=\left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right)^\frac{1}{2}$

The momentum of the recoil electron $p_{e}=p$

The energy of an electron at rest $E_{r}=m_{\circ}c^{2}$

The momentum of an electron at rest $p_{r}=0$

According to the energy conservation principle,

The total energy of an electron and an X-ray photon before the collision = The total energy of an electron and an X-ray photon after the collision

$E_{i}+E_{r}= E_{e}+E_{s}$

$h\nu + m_{\circ}c^{2} = \left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right)^\frac{1}{2} + h\nu'$

$\left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right)^\frac{1}{2} = h\nu - h\nu' + m_{\circ}c^{2}$

$\left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right)^\frac{1}{2} = h \left( \nu - \nu' \right) + m_{\circ}c^{2}$

Square the above equation

$\left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right) = \left[ h \left( \nu - \nu' \right) + m_{\circ}c^{2} \right]^{2}$

$p^{2}c^{2} + m_{\circ}^{2}c^{4} = h^{2} \left( \nu - \nu' \right)^{2} + m_{\circ}^{2}c^{4} + 2 h \left( \nu - \nu' \right) m_{\circ}c^{2}$

$p^{2}c^{2} = h^{2} \left( \nu - \nu' \right)^{2} + 2 h \left( \nu - \nu' \right) m_{\circ}c^{2}$

$\frac{p^{2}c^{2}}{h^{2}} = \left( \nu - \nu' \right)^{2} + \frac{2m_{\circ}c^{2}}{h} \left( \nu - \nu' \right) \qquad(1)$

Momentum is a vector quantity and it is conserved for elastic collision in each of two mutually perpendicular directions.

Total momentum along the direction of the incident photon:

$p\: cos\phi + \frac{h\nu'}{c} \: cos\theta=\frac{h\nu}{c}$

$p\: cos\phi =\frac{h\nu}{c} - \frac{h\nu'}{c} \: cos\theta$

$\frac{pc}{h}\: cos\phi =\nu - \nu'\: cos\theta \qquad(2)$

Total momentum at the right angle to the direction of the incident photon:

$p\:sin\phi=\frac{h\nu'}{c}sin\theta$

$\frac{pc}{h}\: sin\phi =\nu'\: sin\theta \qquad(3)$

To eliminate $\phi$, square the equation $(2)$ and equation $(3)$ and then add them. This gives

$\frac{p^{2}c^{2}}{h^{2}}\: cos^{2}\phi + \frac{p^{2}c^{2}}{h^{2}}\: sin^{2}\phi = \left(\nu - \nu'\: cos\theta \right)^{2}+ \nu'^{2}\: sin^{2}\theta $

$\frac{p^{2}c^{2}}{h^{2}} \left(sin^{2}\phi + cos^{2}\phi \right) = \left(\nu - \nu'\: cos\theta \right)^{2}+ \nu'^{2}\: sin^{2}\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \left(\nu - \nu'\: cos\theta \right)^{2}+ \nu'^{2}\: sin^{2}\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2}\: cos^{2}\theta - 2 \nu \nu' \:cos\theta + \nu'^{2}\: sin^{2}\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2} \left(sin^{2}\theta + cos^{2}\theta \right) - 2 \nu \nu' \:cos\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2} - 2 \nu \nu' \:cos\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2} - 2 \nu \nu'+ 2 \nu \nu' - 2 \nu \nu' \:cos\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \left(\nu - \nu' \right)^{2} + 2 \nu \nu' - 2 \nu \nu' \:cos\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \left(\nu - \nu' \right)^{2} + 2 \nu \nu'\left(1 - cos\theta \right) \quad(4) $

Equation $(1)$ and equation $(4)$ left-hand sides are equal, So equate their right-hand sides, then we get

$ \left( \nu - \nu' \right)^{2} + \frac{2m_{\circ}c^{2}}{h} \left( \nu - \nu' \right) = \left(\nu - \nu' \right)^{2} + 2 \nu \nu'\left(1 - cos\theta \right)$

$ \frac{2m_{\circ}c^{2}}{h} \left( \nu - \nu' \right) = 2 \nu \nu'\left(1 - cos\theta \right)$

$ \frac{\left( \nu - \nu' \right)}{\nu\nu'} = \frac{h}{m_{\circ}c^{2}} \left(1 - cos\theta \right)$

$ \frac{1}{\nu'}-\frac{1}{\nu} = \frac{h}{m_{\circ}c^{2}} \left(1 - cos\theta \right) \qquad(5)$

$ \frac{c}{\nu'}-\frac{c}{\nu} = \frac{hc}{m_{\circ}c^{2}} \left(1 - cos\theta \right)$

$ \frac{c}{\nu'}-\frac{c}{\nu} = \frac{h}{m_{\circ}c} \left(1 - cos\theta \right)$

$ \lambda'-\lambda = \frac{h}{m_{\circ}c} \left(1 - cos\theta \right) $

$ \Delta \lambda = \lambda'-\lambda = \frac{h}{m_{\circ}c} \left(1 - cos\theta \right) \qquad(6)$

$ \Delta \lambda = \lambda'-\lambda = \frac{2h}{m_{\circ}c} cos^{2}\theta \qquad(7)$

Here the equation $(6)$ and equation $(7)$ is the expression for the Compton Shift in the wavelength of the X-rays, scattered by electrons in a low atomic number material.

The quantity $\frac{h}{2m_{\circ}c}$ is called the "Compton wavelength" of the electron and denoted by $\lambda_{e}$. The numerical value of $\frac{h}{2m_{\circ}c}$ is $0.2426 \times 10^{-11}$ or $0.02426 A^{\circ}$. Now substitute this value in the above equation $(6)$ and equation $(7)$. Therefore

$ \Delta \lambda = \lambda'-\lambda = \lambda_{e} \left(1 - cos\theta \right) \: A^{\circ}$

$ \Delta \lambda = \lambda'-\lambda = 0.02426 \left(1 - cos\theta \right) \: A^{\circ}$

$ \Delta \lambda = \lambda'-\lambda = 2 \lambda_{e} \: cos^{2}\theta \: A^{\circ}$

$ \Delta \lambda = \lambda'-\lambda = 0.04852 \: cos^{2}\theta \: A^{\circ}$

Thus, this theoretical expression derived by Compton is in excellent agreement with this experimental result.

The expression $\Delta \lambda$ leads to the following conclusion:

i.) The wavelength of the radiation scattered at different angles $\theta$ is always greater than the wavelength of the incident radiation.

ii.) The wavelength shifts $\Delta \lambda$ is independent of the wavelength of the incident X-ray, and at a fixed angle of scattering it is the same for all substances containing unbound electrons at rest.

iii.) The wavelength shift increases with the angle of scattering $\theta$ and it has a maximum value equal to $\frac{2h}{m_{\circ}c}$ when $\theta=180^{\circ}$.

4.) Limitation of Compton Effect:

i.) The Compton theory does not explain the presence of X-rays of the same wavelength in the scattered radiation, as the incident rays.

An explanation for this unmodified scattered radiation is as follows:

The incident X-ray photons collide with loosely bound outer electrons and also with tightly bound inner electrons of the atm. During a collision of a photon with tightly bound electrons, the electron is not detached from the atom. Consequently the entire atom recoils. In such a collision the Compton shift of the wavelength is given by replacing $m_{\circ}$ by the mass of the atom in equation $(7)$. Calculations show that this shift is so small that it can not be detected because the mass of an atom is usually several thousand times greater than the mass of the electron at rest.

For Example, The Graphite scattered the mass $M$ of the atom is

$M=12 \times 1840 \times m_{\circ}$

The maximum value of the Compton shift due to the collision of photons with bound electrons of graphite atoms is

$\Delta \lambda = \frac{2h}{Mc} \: sin^{2} \frac{\theta}{2}$

$\Delta \lambda = \frac{2}{12 \times 1840} \left( \frac{h}{m_{\circ}c} \right) \: sin^{2} \frac{180^{\circ}}{2}$

$\Delta \lambda = 9.058 \times 10^{-5} \times 0.02426 A^{\circ}$

$\Delta \lambda = 2.197 \times 10^{-6} A^{\circ}$

Thus the $\Delta \lambda$ is negligible.

ii.) It has been observed that the intensity of the modified X-rays is greater than that of unmodified X-rays for low atomic number materials. But for heavier materials i.e. high atomic number materials the reverse observation has been obtained. These results are not explained by the Compton theory.

5.) Compton Recoil Electron:

To study the direction $\phi$ of ejection of the recoil electron and its energy we derive the following expression

5(a) Relation between $\theta$ and $\phi$:

From the Compton theory, from equation $(5)$ we have

$ \frac{1}{\nu'}-\frac{1}{\nu} = \frac{h}{m_{\circ}c^{2}} \left(1 - cos\theta \right) $

$ \frac{\nu}{\nu'}-1 = \frac{h \nu}{m_{\circ}c^{2}} \left(1 - cos\theta \right) $

Let $\alpha =\frac{h \nu}{m_{\circ}c^{2}}$, then above equation can be written as

$ \frac{\nu}{\nu'}-1 = \alpha \left(1 - cos\theta \right) $

$ \frac{\nu}{\nu'} = 1 + \alpha \left(1 - cos\theta \right) \qquad(8) $

Now from equation $(2)$ and equation $(3)$

$\frac{pc}{h}\: cos\phi =\nu - \nu'\: cos\theta$

$\frac{pc}{h}\: sin\phi =\nu'\: sin\theta $

Now divide the above equation:

$cot\phi = \frac{\nu - \nu'\: cos\theta}{\nu'\: sin\theta}$

$cot\phi = \frac{1}{sin \theta} \left ( \frac{\nu}{\nu'} - cos \theta \right)$

Now substitute the value $\frac{\nu}{\nu'}$ form equation $(8)$ in above equation

$cot\phi = \frac{1}{sin \theta} \left[ 1 + \alpha \left(1 - cos\theta \right) - cos \theta \right]$

$cot\phi = \frac{\left( 1 + \alpha \right) \left( 1 - cos\theta \right)}{sin \theta}$

$cot\phi = \frac{\left( 1 + \alpha \right) \left( 2 sin^{2}\frac{\theta}{2} \right)}{2 sin \frac{\theta}{2} cos\frac{\theta}{2}} $

$cot\phi = \frac{\left( 1 + \alpha \right) \left( sin\frac{\theta}{2} \right)}{cos\frac{\theta}{2}} $

$cot\phi = \left( 1 + \alpha \right) tan\frac{\theta}{2} \qquad(9)$

This equation shows that the maximum value of $\phi=90^{\circ}$, when $\theta=0^{\circ}$. Therefore, the recoil electrons ejected at angles $\phi$ less than $90^{\circ}$.

5(b) Kinetic Energy of the Recoil Electron:

The kinetic energy of recoil electron $(E)$ is the difference between the kinetic energy of incident photon $(h\nu)$ and the kinetic energy of the scattered photon $(h\nu')$. i.e

$E=h\nu-h\nu' \qquad(10)$

Now from equation $(8)$

$ \frac{\nu}{\nu'} = 1 + \alpha \left(1 - cos\theta \right) $

$ \nu' = \frac{\nu}{1 + \alpha \left(1 - cos\theta \right)} $

Now subtitute the value of $\nu'$ in equation $(10)$, so we get

$E=h\nu-\frac{h \nu}{1 + \alpha \left(1 - cos\theta \right)}$

$E=h\nu \left[1-\frac{1}{1 + \alpha \left(1 - cos\theta \right)} \right]$

$E=h\nu \left[\frac{1 + \alpha \left(1 - cos\theta \right) -1}{1 + \alpha \left(1 - cos\theta \right)} \right]$

$E=h\nu \left[\frac{\alpha \left(1 - cos\theta \right)}{1 + \alpha \left(1 - cos\theta \right)} \right] \qquad(11)$

$E=h\nu \left[\frac{\alpha \left(2sin^{2}\frac{\theta}{2} \right)}{1 + \alpha \left(2sin^{2}\frac{\theta}{2} \right)} \right]$

$E=h\nu \left[\frac{2\alpha}{cosec^{2} \frac{\theta}{2} +2 \alpha} \right] \qquad(12)$

The right-hand side of the above equation can be expressed in terms of $\phi$. Now from equation $(9)$

$cot\phi = \left( 1 + \alpha \right) tan\frac{\theta}{2}$

$\frac{1}{tan \phi}= \left( 1 + \alpha \right) \frac{1}{cot \frac{\theta}{2}}$

$cot \frac{\theta}{2}= \left( 1 + \alpha \right) \: tan \phi $

Now squaring the above equation

$cot^{2} \frac{\theta}{2}= \left( 1 + \alpha \right)^{2} \: tan^{2} \phi $

$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} \left( sec^{2}\phi -1 \right) $

$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} sec^{2}\phi - \left( 1 + \alpha \right)^{2}$

$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} sec^{2}\phi - \left( 1 + \alpha^{2}+ 2\alpha \right)$

$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} sec^{2}\phi - 1 - \alpha^{2} - 2\alpha $

$cosec^{2} \frac{\theta}{2} + 2\alpha = \left( 1 + \alpha \right)^{2} sec^{2}\phi - \alpha^{2} $

Now substitute the value of the above equation in equation $(12)$, then we get

$E=h\nu \left[\frac{2\alpha}{\left( 1 + \alpha \right)^{2} sec^{2}\phi - \alpha^{2}} \right] $

$E=h\nu \left[\frac{2\alpha \: cos^{2}\phi}{\left( 1 + \alpha \right)^{2} - \alpha^{2} \: cos^{2}\phi} \right] $

The experimental value of $E$ of recoil electrons determined by Compton and Simon in $1925$ and by Bless in $1927$ agreed well with the theoretical value.

The study of the Compton effect leads to the conclusion that radiant energy in its interaction with matter behaves as a stream of discrete particles (Photons) each having energy $h\nu$ and momentum $\frac{h\nu}{c}$. In other words, radiant energy is quantized. Therefore the Compton effect is considered a decisive phenomenon in support of the quantization of energy.

Read More

Inadequacy of classical mechanics

Classical mechanics is a branch of physics that deals with the motion of macroscopic bodies or objects $(i.e \: the \: size \: range \: greater \: then \: 10^{-8}m)$ under the influence of forces. While it was groundbreaking when first developed by Sir Isaac Newton in the 17th century, it has certain limitations that were discovered over time. In this answer, we will discuss these limitations in more detail:

1. Classical Mechanics is not applicable to extremely small objects: Classical mechanics assumes that particles have a definite position and momentum, which is not true in the quantum world. This limitation became apparent in the early 20th century with the discovery of quantum mechanics. Quantum mechanics is a branch of physics that deals with the behavior or motion of particles on an atomic and subatomic level $(i.e \: the \: size \: range \: is \: in \: between \: 10^{-8}m \: to \: 10^{-15}m)$ i.e microscopic particles. It has been successful in explaining phenomena such as the photoelectric effect, blackbody radiation, and the behavior of electrons in atoms, which cannot be explained by classical mechanics.
2. Classical Mechanics is not applicable to objects moving at very high speeds: Classical mechanics assumes that the speed of an object can be infinite,  it is not true in the relativistic world. The theory of relativity which was developed by Albert Einstein in the early 20th century, explains the behavior of objects moving at high speeds (i.e. equal to the speed of light). The theory of relativity has been successful in predicting phenomena such as time dilation, length contraction, and the equivalence of mass and energy.
3. Classical Mechanics can not well explain the behavior of systems with many particles: Classical mechanics is not well suited for dealing with systems that have many particles. This is because it is difficult to solve the equations of motion for systems with many particles, and the behavior of the system can become chaotic. The theory of statistical mechanics, developed in the late 19th century, addresses this limitation by using probability distributions to describe the behavior of large systems.
4. Classical Mechanics can not explain the behavior of objects that are very far apart or have very high masses: Newton's law of gravity works well for objects that are close together, but it fails to explain the behavior of objects that are extremely far apart or have very high masses, such as black holes and galaxies. The theory of general relativity, developed by Einstein in the early 20th century, provides a better explanation of the behavior of objects with very high masses and gravitational fields.
5. Classical Mechanics assumes determinism: Classical mechanics assumes that the universe is deterministic, meaning that the future state of a system can be predicted with complete accuracy if the initial state is known. However, this assumption has been challenged by the theory of chaos, which suggests that small changes in the initial state of a system can lead to unpredictable and chaotic behavior in the future.

In summary, while classical mechanics is still useful for understanding the behavior of macroscopic objects, its limitations have led to the development of new theories, such as quantum mechanics, relativity, statistical mechanics, and chaos theory, which can explain the behavior of the universe at different scales and levels of complexity.

Read More

Momentum wave function for a free particle

A non-relativistic free particle of mass $m$ moving in the positive $x$-direction with speed $v_{x}$ has kinetic energy

$E=\frac{1}{2} m v^{2}_{x}$

and momentum

$p_{x}=mv_{x}$

The energy and momentum are associated with a wave of wavelength $\lambda$ and frequency $\nu$ given by

$\lambda = \frac{h}{p_{x}}$

and

$\nu=\frac{E}{h}$

The propagation constant $k_{x}$ of the wave is

$k_{x}= \frac{2\pi}{\lambda}=\frac{2\pi}{\left(\frac{h}{p_{x}} \right)}=\frac{p_{x}}{\left(\frac{h}{2\pi} \right)}=\frac{p_{x}}{\hbar}$

and the angular frequency $\omega$ is

$\omega = 2\pi \nu = \frac{2\pi E}{\hbar}=\frac{E}{\hbar}$

A plane wave traveling along the $x$ axis in the positive direction may be represented by

$\psi(x,t)=A e^{-i\left(k_{x} \: x - \omega t\right)}$

Now subtitute the value of $\omega$ and $k_{x}$ in above equation then we get

$\psi(x,t)=A e^{i\left( \frac{p_{x}}{\hbar} \: x - \frac{E}{\hbar} \: t\right)}$

$\psi(x,t)=A e^{\frac{i}{\hbar}\left( p_{x} \: x - E \: t\right)}$

The superposition of a number of such waves of propagation number slightly different from an average value traveling simultaneously along the same line in the positive $x$- direction forms a wave packet of small extension. By Fourier's theorem the eave packet may be expressed by

$\psi(x,t) = \frac{1}{\sqrt{2 \pi \hbar}} \int_{-\infty}^{+\infty} A (p_{x}) e^{\frac{i}{\hbar}\left( p_{x} \: x - E \: t \right)} \: \: dp_{x} \qquad(1)$

The function $\psi(x,t)$ is called the momentum wave function for the motion of the free particle in one dimension.

The amplitude $A(p_{x})$ of the $x$-component of the momentum is given by the Fourier tranform

$A(p)=\frac{1}{\sqrt{2 \pi \hbar}} \int_{-\infty}^{+\infty} \psi (x,t) e^{-\frac{i}{\hbar}\left( p_{x} \: x - E \: t \right)} \: \: dx \qquad(2)$

In three dimension the wave function is represented by

$\psi(\overrightarrow{r},t) = \frac{1}{(2 \pi \hbar)^{3/2}} \int_{-\infty}^{+\infty} A (\overrightarrow{p}) e^{\frac{i}{\hbar}\left( \overrightarrow{p} . \overrightarrow{r} - E \: t \right)} \: \: d^{3}\overrightarrow{p} \qquad(3)$

Where $d^{3}\overrightarrow{p}=dp_{x} \: dp_{y} \: dp_{z}$ is the volume element in the momentum space. In equation $(1)$, equation $(2)$ and equation $(3)$ $\frac{1}{\sqrt{2 \pi \hbar}}$ and $\frac{1}{(2 \pi \hbar)^{3/2}}$ are normalization constants.

Read More

Schrodinger's equation for the complex conjugate waves function

Derivation:

The time dependent Schrodinger quation for the wave function function $psi(x,y,z,t)$ is

$-\frac{\hbar^{2}}{2m}\nabla^{2} \psi + V\psi=i\hbar\frac{\partial \psi}{\partial t} \qquad(1)$

Since wave function, $\psi$ is complex quantity i.e.

$\psi=\psi_{1}+i \: \psi_{2} \qquad(2)$

Where $\psi_{1}$ and $\psi_{2}$ are real functions of $x,y,z,t$. Substituting this form for $\psi$ in equation $(1)$, we get

$-\frac{\hbar^{2}}{2m}\nabla^{2} \left( \psi_{1}+i \: \psi_{2} \right) + V\left( \psi_{1}+i \: \psi_{2} \right) \\ \qquad = i\hbar\frac{\partial }{\partial t} \left( \psi_{1}+i \: \psi_{2} \right)$

Equation real and imaginary parts on either side of this equation, we obtain the following two equations:

$-\frac{\hbar^{2}}{2m}\nabla^{2} \psi_{1} + V\psi_{1}=-\hbar\frac{\partial \psi_{2}}{\partial t} \qquad(3)$

$-\frac{\hbar^{2}}{2m}\nabla^{2} \psi_{2} + V\psi_{2}=\hbar\frac{\partial \psi_{1}}{\partial t} \qquad(4)$

Mutiplying equation $(4)$ by $-i$ and adding it to equation $(3)$, we get

$-\frac{\hbar^{2}}{2m}\nabla^{2} \left( \psi_{1} - i \: \psi_{2} \right) + V\left( \psi_{1} - i \: \psi_{2} \right) \\ \qquad = -i\hbar\frac{\partial }{\partial t} \left( \psi_{1} - i \: \psi_{2} \right) \qquad(5)$

The complex conjugate of wave function $\psi^{*}$ is

$\psi^{*}=\psi^{*}_{1} - i \: \psi^{*}_{2} \qquad(6)$

Therefore, The equation $(5)$ can be written as

$-\frac{\hbar^{2}}{2m}\nabla^{2} \psi^{*} + V \psi^{*} =-i \hbar \frac{\partial \psi^{*}}{\partial t}$

This is the equation for complex conjugate wave function $\psi^{*}$.

Read More

Probability Current Density for a free particle in Quantum Mechanics

1.) Derivation of Probability Current Density for a free particle:

Let a particle of mass $m$ is moving in the positive $x$- direction in the region from $x_{1}$ to $x_{2}$.

For the one-dimensional motion of the particle, the wave function is $psi(x,t)$ Let $dA$ be the area of the cross-section of the region.

The probability of finding a particle in the region is

$\int_{x_{1}}^{x_{2}} \psi(x,t) \: \psi^{*}(x,t) \: dx \: dA \qquad(1)$

and the probability density of finding the particle in the region is

$P=\psi(x,t) \: \psi^{*}(x,t) \qquad(2)$

If the probability of finding the particle in the region decreases with time, the rate of decrease of the probability that the particle is in the region from $x_{1}$ to $x_{2}$ per unit area is called the probability current density out of the region. Therefore, the probability current density $S_{2} - S_{1}$ out of the region in the positive $x$-direction is given by

$S_{2} - S_{1} = - \frac{1}{dA} \left[- \frac{d}{dt} \int_{x_{1}}^{x_{2}} P \: dx \: dA \right]$

$S_{2} - S_{1} = - \frac{\partial}{\partial t} \int_{x_{1}}^{x_{2}} P \: dx $

$S_{2} - S_{1} = - \frac{\partial}{\partial t} \int_{x_{1}}^{x_{2}} \psi(x,t) \: \psi^{*}(x,t) \: dx \qquad(3)$

And the probability of current density at position $x$ is

$S = - \frac{\partial}{\partial t} \int \psi(x,t) \: \psi^{*}(x,t) \: dx \qquad(4)$

1.1) Show that: $S = \frac{i \hbar}{2m} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right]$

Proof:

According to the Schrodinger equation for wave function $\psi(x,t)$ and $\psi^{*}(x,t)$ are

$i \hbar \frac{\partial \psi}{\partial t} =- \frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi}{\partial x^{2}} + V \psi \qquad(1.1.1)$

The complex conjugate of the wave function

$-i \hbar \frac{\partial \psi^{*}}{\partial t} = -\frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi^{*}}{\partial x^{2}} + V \psi^{*} \qquad(1.1.2)$

Multiplying equation $(1.1.1)$ by $\psi^{*}$ and equation $(1.1.2)$ by $\psi$, we get

$i \hbar \psi^{*} \frac{\partial \psi}{\partial t} =- \frac{\hbar^{2}}{2m} \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} + \psi^{*} V \psi \quad(1.1.3)$

$-i \hbar \psi \frac{\partial \psi^{*}}{\partial t} = -\frac{\hbar^{2}}{2m} \psi \frac{\partial^{2} \psi^{*}}{\partial x^{2}} + \psi V \psi^{*} \quad(1.1.4)$

Now subtracting equation $(1.1.4)$ and equation $(1.1.3)$, we get

$i \hbar \left( \psi^{*} \frac{\partial \psi}{\partial t} + \psi \frac{\partial \psi^{*}}{\partial t} \right) =-\frac{\hbar^{2}}{2m} \left[ \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} - \psi \frac{\partial^{2} \psi^{*}}{\partial x^{2}} \right]$

$i \hbar \frac{\partial}{\partial t} \left( \psi \psi^{*} \right) =-\frac{\hbar^{2}}{2m} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right]$

$ \frac{\partial}{\partial t} \left( \psi \psi^{*} \right) =\frac{i\hbar}{2m} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right] \quad(1.1.5)$

We know that

$S = - \frac{\partial}{\partial t} \int \psi(x,t) \: \psi^{*}(x,t) \: dx $

Now substitute the value of equation $(9)$ in the above equation that can be written as

$ S = -\frac{i\hbar}{2m} \int \frac{\partial}{\partial x} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right] dx $

$ S = -\frac{i\hbar}{2m} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right] $

1.2) Show That The probability current density for a free particle is equal to the product of its probability density and its speed.

Proof:

For a free particle that is moving in the positive $x$-axis direction and the momentum $p_{x}$ at position $x$ is given by

$\frac{\hbar}{i} \frac{\partial \psi}{\partial x} = p_{x} \psi$

$ \frac{\partial \psi}{\partial x} = \frac{i}{\hbar} p_{x} \psi \qquad(1.2.1)$

and

$-\frac{\hbar}{i} \frac{\partial \psi^{*}}{\partial x} = p_{x} \psi^{*}$

$ \frac{\partial \psi^{*}}{\partial x} = - \frac{i}{\hbar} p_{x} \psi^{*} \qquad(1.2.2)$

We know that

$ S = -\frac{i\hbar}{2m} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right] $

Now substitute the value of equation $(1.2.1)$ and equation $(1.2.2)$ in the above equation, we get

$ S = -\frac{i\hbar}{2m} \left[ \psi^{*} \frac{i}{\hbar} p_{x} \psi + \psi \frac{i}{\hbar} p_{x} \psi^{*}\right] $

$ S = \frac{1}{2m} \left[ \psi^{*} p_{x} \psi + \psi p_{x} \psi^{*}\right] $

$ S = \frac{1}{m} \left( \psi \psi^{*} p_{x} \right)$

$ S = \frac{ p_{x} }{m} \left( \psi \psi^{*}\right) \qquad(1.2.3) $

Now put $p_{x}= m v_{x}$ in equation $(1.2.3)$

$ S = \frac{m v_{x} }{m} \left( \psi \psi^{*}\right)$

$ S = \left( \psi \psi^{*}\right) v_{x}$

Now put $p_{x}= \hbar k_{x}$ in equation $(1.2.3)$

$ S = \frac{ \hbar \: k_{x} }{m} \left( \psi \psi^{*}\right) $

Read More

Ehrenfest's Theorem and Derivation

Ehrenfest's Theorem Statement:

The theorem states that

Quantum mechanics gives the same results as classical mechanics for a particle for which average or expectation values of dynamical quantities are involved.

Proof of theorem:

The proof of the theorem for one-dimensional motion of a particle by showing that

1) $\frac{d \left < x \right >}{dt} = \frac{\left < p_{x} \right > }{m}$

2) $\frac{d \left < p_{x} \right >}{dt} = \left < F_{x} \right >$

1.) To Show that: $\frac{d \left < x \right > }{dt} = \frac{\left < p_{x} \right > }{m}$

Let $x$ is the position coordinate of a particle of mass $m$, at time $t$

The expectation value of position $x$ of a particle is given by

$\left < x \right > = \int_{- \infty}^{+ \infty} \psi^{*} (x,t) . x \: \psi (x,t) dx \qquad (1)$

Differentiating the above equation $(1)$ with respect to $t$

$\frac{d \left < x \right > }{dt} = \int_{- \infty}^{+ \infty} x \frac{\partial (\psi \psi^{*})}{\partial t} dx \qquad(2)$

We know the probablity current density

$\frac{\partial (\psi \psi^{*})}{\partial t} = \frac{i \hbar}{2m} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right] \qquad(3)$

Now substitute the above eqaution$(3)$ in eqaution $(2)$

$\frac{d \left < x \right > }{dt} = \frac{i \hbar}{2m} \int_{- \infty}^{+ \infty} x \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right] dx $

Integrating the right-hand side by parts of the above equation, we get

$\frac{d \left < x \right > }{dt} = \frac{i \hbar}{2m} \left[ x \left( \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right) \right]^{+\infty}_{-\infty} \\ \qquad - \frac{i \hbar}{2m} \int_{- \infty}^{+ \infty} \left( \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right) dx $

As $x$ approaches either $+ \infty$ or $-\infty$, $\psi$ and $\frac{\partial \psi}{\partial x}$ approach zero, and therefore the first term becomes zero.

Hence we get

$\frac{d \left < x \right > }{dt} = - \frac{i \hbar}{2m} \int_{- \infty}^{+ \infty} \left( \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right) dx \\ \qquad\qquad\qquad\qquad\qquad\qquad ---(4)$

The expectation value of $p_{x}$ is given by

$ \left < p_{x} \right > = \int_{- \infty}^{+ \infty} \psi^{*} \frac{\hbar}{i} \frac{\partial \psi}{\partial x} $

$ \int_{- \infty}^{+ \infty} \psi^{*} \frac{\partial \psi}{\partial x} dx = \frac{i}{\hbar}\left < p_{x} \right > \qquad(5)$

Similarly

$ \int_{- \infty}^{+ \infty} \psi \frac{\partial \psi^{*}}{\partial x} dx = - \frac{i}{\hbar}\left < p_{x} \right > \qquad(6)$

Substituting the values of these integrals in equation $(4)$

$\frac{d \left < x \right > }{dt} = - \frac{i \hbar}{2m} \left[ \frac{i}{\hbar}\left < p_{x} \right > + \frac{i}{\hbar}\left < p_{x} \right >\right] $

$\frac{d \left < x \right > }{dt} = - \frac{\left < p_{x} \right >}{m} \qquad(7)$

This is the first result of Ehrenfest's Theorem.

2) To show that: $\frac{d \left < p_{x} \right >}{dt} = \left < F_{x} \right >$

We know that the expectation value of the momentum $p_{x}$ is given by

$ \left < p_{x} \right > = \int_{- \infty}^{+ \infty} \psi^{*} \frac{\hbar}{i} \frac{\partial \psi}{\partial x} $

$ \left < p_{x} \right > =\frac{\hbar}{i} \int_{- \infty}^{+ \infty} \psi^{*} \frac{\partial \psi}{\partial x} \qquad(8)$

Differentiating the equation $(8)$ with respect to $t$, we get

$\frac{d \left < p_{x} \right >}{dt} = \frac{\hbar}{i} \int_{- \infty}^{+ \infty} \left[ \frac{\partial \psi^{*}}{\partial t} \frac{\partial \psi}{\partial x} + \psi^{*} \frac{\partial^{2} \psi}{\partial x \partial t} \right] $

$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left[-i \hbar \frac{\partial \psi^{*}}{\partial t} \frac{\partial \psi}{\partial x} - i\hbar \psi^{*} \frac{\partial^{2} \psi}{\partial x \partial t} \right] \\ \qquad\qquad\qquad\qquad\qquad\qquad ---(9)$

Now the time-dependent Schrodinger equations for $\psi$ and $\psi^{*}$ are

$i \hbar \frac{\partial \psi}{\partial t} =- \frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi}{\partial x^{2}} + V \psi \qquad(10)$

The complex conjugate of Schrodinger function

$-i \hbar \frac{\partial \psi^{*}}{\partial t} = -\frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi^{*}}{\partial x^{2}} + V \psi^{*} \qquad(11)$

Differentiating the equation $(10)$ with respect to $x$

$i \hbar \frac{\partial^{2} \psi}{\partial x \partial t} = - \frac{\hbar^{2}}{2m} \frac{\partial^{3} \psi}{\partial x^{3}} + \frac{\partial (V \psi)}{\partial x} \qquad(12)$

Now substitute the value of $-i \hbar \frac{\partial \psi^{*}}{\partial t}$ and $i \hbar \frac{\partial^{2} \psi}{\partial x \partial t}$ in the equation $(9)$, we get

$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left[ \left( -\frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi^{*}}{\partial x^{2}} + V \psi^{*} \right) \frac{\partial \psi}{\partial x} - \psi^{*} \left( - \frac{\hbar^{2}}{2m} \frac{\partial^{3} \psi}{\partial x^{3}} + \frac{\partial (V \psi)}{\partial x} \right) \right]$

$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left[-\frac{\hbar^{2}}{2m} \left( \frac{\partial^{2} \psi^{*}}{\partial x^{2}}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{3} \psi}{\partial x^{3}} \right) - \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial (V \psi)}{\partial x} \right) \right] dx$

$\frac{d \left < p_{x} \right >}{dt} = -\frac{\hbar^{2}}{2m} \int_{- \infty}^{+ \infty} \left( \frac{\partial^{2} \psi^{*}}{\partial x^{2}}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{3} \psi}{\partial x^{3}} \right) dx + \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial (V \psi)}{\partial x} \right) dx$

$\frac{d \left < p_{x} \right >}{dt} = -\frac{\hbar^{2}}{2m} \int_{- \infty}^{+ \infty} \frac{\partial}{\partial x} \left( \frac{\partial \psi^{*}}{\partial x}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} \right) dx + \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial (V \psi)}{\partial x} \right) dx$

Now put $\frac{\partial (V \psi)}{\partial x}= \left\{ \psi \frac{\partial V }{\partial x}+ V\frac{\partial \psi}{\partial x} \right\}$ in above equation:

$\frac{d \left < p_{x} \right >}{dt} = -\frac{\hbar^{2}}{2m} \int_{- \infty}^{+ \infty} \frac{\partial}{\partial x} \left( \frac{\partial \psi^{*}}{\partial x}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} \right) dx + \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \left\{ \psi \frac{\partial V }{\partial x}+ V\frac{\partial \psi}{\partial x} \right\} \right) dx$

$\frac{d \left < p_{x} \right >}{dt} = -\frac{\hbar^{2}}{2m} \left[ \frac{\partial \psi^{*}}{\partial x}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} \right]_{- \infty}^{+ \infty} + \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \left\{ \psi \frac{\partial V }{\partial x}+ V\frac{\partial \psi}{\partial x} \right\} \right) dx$

As $x$ approaches either $+ \infty $ or $-\infty$ and $\frac{\partial \psi}{\partial x}$ is zero. Therefore the first term of the above equation on the right-hand side will be zero.

$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \left\{ \psi \frac{\partial V }{\partial x}+ V\frac{\partial \psi}{\partial x} \right\} \right) dx$

$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial V }{\partial x} \psi^{*} - V \psi^{*} \frac{\partial \psi}{\partial x} \right) dx$

$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} - \psi \frac{\partial V }{\partial x} \psi^{*} dx$

$\frac{d \left < p_{x} \right >}{dt} = - \int_{- \infty}^{+ \infty} \psi \frac{\partial V }{\partial x} \psi^{*} dx$

$\frac{d \left < p_{x} \right >}{dt} = -\left < \frac{\partial V }{\partial x} \right > $

Here the $\left < \frac{\partial V }{\partial x} \right >$ is the average value or expectation value of potential gradient and the negative value of the potential gradient is equal to the average value or expectation value of force $\left < F_{x} \right >$ along the $x$ direction.

$\frac{d \left < p_{x} \right >}{dt} = \left < F_{x} \right > $

This is the second result of Ehrenfest theorem and it represents Newton's second law of motion. Thus if the expectation values of dynamical quantities for a particle are, considered, quantum mechanics given the equations of classical mechanics.

Read More

Eigen value of the momentum of a particle in one dimension box or infinite potential well

Equation of eigen value of the momentum of a particle in one dimension box:

The eigen value of the momentum $P_{n}$ of a particle in one dimension box moving along the x-axis is given by

$P^{2}_{n} = 2 m E_{n}$

$P^{2}_{n} = 2 m \frac{n^{2} \pi^{2} \hbar^{2}}{2 m L^{2}} \qquad \left( \because E_{n}= \frac{n^{2} \pi^{2} \hbar^{2}}{2 m L^{2}} \right)$

$P^{2}_{n} = \frac{n^{2} \pi^{2} \hbar^{2}}{L^{2}}$

$P_{n} = \pm \frac{n \pi \hbar}{L}$

$P_{n} = \pm \frac{n h}{2L} \qquad \left( \hbar = \frac{h}{2 \pi} \right)$

The $\pm$ sign indicates that the particle is moving back and forth in the infinite potential box.

The above equation shows that eigen value of the momentum of the particle is discrete and the difference between the momentum corresponding to two consecutive energy levels is always constant and equal to $\frac{h}{2L}$

Read More

Derivation of Planck's Radiation Law

Derivation: Let $ N$ be the total number of Planck’s oscillators and $E$ be their total energy, then the average energy per Planck’s oscillator is

$ \overline{E}=\frac{E_{N}}{N} \qquad (1)$

Let there be $ N_{0}, N_{1} ,N_{2} ,N_{3},---N_{n}$ oscillator having energy $ E_{0}, E_{1}, E_{2}, -- E_{n}$ respectively.

According to Maxwell’s distribution, the number of oscillators in the $ n^{th}$ energy state is related to the number of oscillators in the ground state by

$ N_{n}=N _{0} e^{\tfrac{-nh\nu }{kt} }\qquad (2)$

Where $ n$ is a positive integer. So put $ n= 1,2,3,…….$. The above equation can be written for different energy states. i.e.

$ N_{1}= N _{0} e^{\tfrac{-h\nu }{kt} }$

$ N_{2}= N _{0} e^{\tfrac{-2h\nu }{kt} }$

$ N_{3}= N _{0} e^{\tfrac{-3h\nu }{kt} }$

$.............$

$.............$

So, the total number of Planck’s Oscillators –

$ N= N _{0} +N_{1}+N_{2}+N_{3}+.... N_{n}$

$ N= N _{0} + N_{0} e^{\tfrac{-h\nu }{kt}}+ N_{0} e^{\tfrac{-2h\nu }{kt}}+...+ N_{0}e^{\tfrac{-nh\nu }{kt}}$

$ N= N _{0}[1+e^{\tfrac{-h\nu }{kt}}+e^{\tfrac{-2h\nu }{kt}}+.... e^{\tfrac{-nh\nu }{kt}}] \qquad(3)$

Let $ x = e^{\frac{-h\nu }{kt}} \qquad (4) $

Then $ N = N_{0}[1+x+x^{2}+x^{3}+...+ x^{n}]$

$ N = \frac{N_{0}}{1-x} \qquad(5)$ [ from Binomial theorem]

Now the total energy of oscillators –

$ E_{N} = E_{0}N_{0}+ E_{1}N_{1}+ E_{2}N_{2}+...+ E_{n}N_{n}$

$ E_{N } = 0.N_{0}+ h\nu N_{0} e^{\tfrac{-h\nu }{kt}}+...+nh\nu N_{0} e^{\tfrac{-nh\nu }{kt}}$

$ E_{N } = N_{0}h\nu (e^{\tfrac{-h\nu }{kt}}+2e^{\tfrac{-2h\nu }{kt}}+...+ ne^{\tfrac{-nh\nu }{kt}})$

From equation $(4)$ put $ x = e^{\tfrac{-h\nu }{kt}}$ in above equation. i.e

$ E_{N } = N_{0}h\nu (x+2x^{2}+3x^{3}+...+nx^{n}) $

$ E_{N } = N_{0}h\nu x(1+2x+3x^{2}+....)$

$ E_{N } = \frac{N_{0}h\nu x}{(1-x)^{2}} \qquad(6)$ (from Bionomical theorem)

Now substituting the value of $N$ from equation $ (5)$ and $ E_{n}$ from equation $ (6)$  in equation $ (1)$ –

$ \overline{E}= \frac{\frac{N_{0}h\nu x}{(1-x)^{2}}}{\frac{N_{0}}{(1-x)}}$

$ \overline{E}= \frac{h\nu }{(\frac{1}{x}-1)}$

$ \overline{E}= \frac{h\nu }{e^{\tfrac{h\nu }{kt}}-1} \qquad(7)$

The number of oscillators per unit volume in wavelength range to $ ( \lambda + d\lambda )$ is $\frac{8\pi }{\lambda ^{4}} d\lambda$.

The energy per unit volume $ (E_{\lambda }d\lambda )$ in the wavelength range to $( \lambda +d\lambda ) $ is –

$ E_{\lambda}d\lambda = \frac{8\pi }{\lambda ^{4}}d\lambda \overline{E} \qquad(8)$

From equation $ (7)$ and $ (8)$ –

$ E_{\lambda}d\lambda = \frac{8\pi }{\lambda ^{4}}d\lambda \frac{h\nu }{(e^{\tfrac{h\nu}{kt}}-1)}$

$ E_{\lambda}d\lambda = \frac{8\pi hc}{\lambda ^{5}} \frac{d\lambda}{(e^{\tfrac{hc}{\lambda kt}}-1)}$

The above equation describes Planck’s radiation law and this law was able to thoroughly explain the black body radiation spectrum.

Wien’s Displacement law from Planck’s Radiation Law:

Planck’s radiation law gives the energy in wavelength region $ \lambda to \lambda +d\lambda $ as –

$ E_{\lambda}d \lambda = \frac{8\pi hc}{\lambda ^{5}}(\frac{1}{e^{\tfrac{hc}{\lambda kt}}-1})d\lambda \qquad(1)$

For shorter wavelength $ \lambda T$ will be small and hence

$ e^{\tfrac{hc}{\lambda kt}}> > 1$

Hence, for a small value of $\lambda T$ Planck’s formula reduces to -

$ E_{\lambda}d \lambda = \frac{8\pi hc}{\lambda ^{5}}(\frac{1}{e^{\tfrac{hc}{\lambda kt}}}) d\lambda$

$ E_{\lambda}d\lambda = \frac{8\pi hc}{\lambda ^{5}}e^{\tfrac{-hc}{\lambda kt}}d\lambda$

$E_{\lambda}d\lambda = A \lambda ^{-5} e^{\tfrac{-hc}{\lambda kt}}d\lambda$

Where $ A = 8\pi hc$

The above equation is Wien’s law of energy distribution verified by Planck radiation law.

Rayleigh-Jeans law from Planck’s Radiation Law:

According to Planck’s radiation law –

$ E_{\lambda}.d\lambda = \frac{8\pi hc}{\lambda ^{5}}\frac{1 }{e^{\tfrac{hc}{\lambda kt}}-1}.d\lambda$

For longer wavelength $ e^{\frac{hc}{\lambda kt}}$ is small and can be expanded as-

$ e^{\tfrac{hc}{\lambda kt}} = 1+\frac{hc}{\lambda kt}+\frac{1}{2!}(\frac{hc}{\lambda kt})^{2}+....$

Neglecting the higher-order term –

$ e^{\tfrac{hc}{\lambda kt}} = 1+\frac{hc}{\lambda kt}$

Hence for longer wavelength, Planck’s formula reduces to –

$ E_{\lambda}.d\lambda = \frac{8\pi kt}{\lambda ^{5}}[\frac{1}{1+\frac{hc}{\lambda kt}-1}]$

$ E_{\lambda}.d\lambda = \frac{8\pi kt}{\lambda ^{4}}.d\lambda$

This is Rayleigh Jean’s law verified by Planck Radiation Law.

Read More