Alternating Current Circuit containing Resistance (R-Circuit): Let us consider, An alternating current circuit containing resistance $R$ only. This resistance $R$ is connected with an alternating EMF i.e electromotive force source i.e.
|
$E=E_{\circ}sin\omega t\qquad(1)$
|
The potential difference across the circuit
$E=iR$
Then from equation $(1)$
$iR=E_{\circ}sin\omega t $
$i=\frac{E_{\circ}}{R}sin\omega t $
|
$i=i_{\circ}sin\omega t \qquad(2) $
|
Where $i_{\circ}$ is the peak value or amplitude of the current in the circuit which has value $i_{\circ}=\frac{E_{\circ}}{R}$.
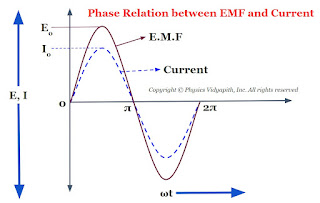
Now compare the equation $(1)$ and equation $(2)$ which shows that if a circuit is containing a resistor only then the current is always in phase with the applied EMF i.e electromotive force. The phase diagram between EMF and the current of resistance is shown below-
The phasor diagram between the EMF and current of resistance is also shown in the given figure below-
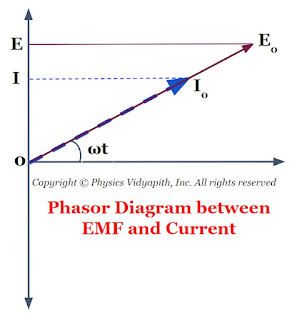
The phasor diagram between the EMF and current of resistance is also shown in the given figure below-
