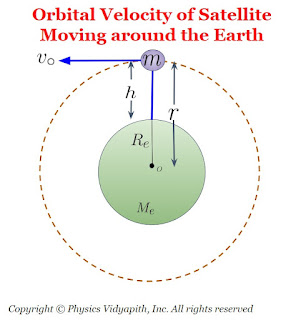
Orbital Velocity of Satellite:
When any satellite moves about the planet in a particular orbit then the velocity of the satellite is called the orbital velocity of the satellite.
Expression for Orbital Velocity of Satellite:
Let us consider:
The mass of the satellite = $m$
The mass of planet= $M$
The radius of Planet =$R$
The satellite is moving about the planet at height=$h$
The satellite is moving about the planet with orbital velocity=$v_{\circ}$
The distance from the center of the planet to satellite=$r$
The force of gravitation between the planet and the satellite
$F=G \frac{M \: m}{r^{2}} \qquad(1)$
This force work act as a centripetal force to revolve the satellite around the planet i.e.
$F=\frac{m v_{\circ}^{2}}{r} \qquad(2)$
From the above equation $(1)$ and equation $(2)$, we get
$\frac{m v_{\circ}^{2}}{r} = G \frac{M \: m}{r^{2}}$
$v_{\circ}= \sqrt{\frac{G \: M }{r}}$
Where $r=R+h$ then
$v_{\circ}= \sqrt{\frac{G \: M }{R+h}} \qquad(3)$
This is the equation of the orbital velocity of the satellite.
If any satellite revolves around the earth then the orbital velocity
$v_{\circ}= \sqrt{\frac{G \: M_{e} }{R_{e}+h}}$
$v_{\circ}= \sqrt{\frac{gR_{e}^{2}}{R_{e}+h}} \qquad \left( \because G \: M_{e} = gR_{e}^{2} \right)$
$v_{\circ}= R_{e} \sqrt{\frac{g}{R_{e}+h}} $
This is the equation of the orbital velocity of a satellite revolving around the earth.
If the satellite is orbiting very close to the surface of the earth ( i.e $h=0$) then the orbital velocity
$v_{\circ}= R_{e} \sqrt{\frac{g}{R_{e}+0}} $
$v_{\circ}= \sqrt{g R_{e}} $
Now subtitute the value of radius of earth (i.e $R_{e}=6.4 \times 10^{6} \: m$) and gravitational accelertaion ($g=9.8 \:m/sec^{2}$) then orbital velocity
$v_{\circ}=7.92 \: Km/sec$
The time period of Revolving Satellite:
The time taken by satellite to complete on revolution around the planet is called the time period of the satellite.
Let us consider the time period of the revolving satellite is $T$ Then
$T= \frac{Distance \: covered \: by \: Satellite \: in \: one \: revolution}{Orbital \: Velocity}$
$T= \frac{2 \pi r}{v_{\circ}}$
$T= \frac{2 \pi \left( R+h \right)}{v_{\circ}}$
$T= \frac{2 \pi \left( R+h \right)}{v_{\circ}}$
Now subtitute the value of orbital velocity $v_{\circ}$ from equation $(3)$ in above equation then
$T= \frac{2 \pi \left( R+h \right)}{\sqrt{\frac{G \: M }{R+h}}}$
$T= 2 \pi \sqrt{ \frac{ \left( R+h \right)^{3}}{G M}}$
This is the equation of the time period of the revolution of satellites.
If a satellite revolves around the earth then the time period
$T= 2 \pi \sqrt{ \frac{ \left( R_{e}+h \right)^{3}}{G M_{e}}}$
$T= 2 \pi \sqrt{ \frac{ \left( R_{e}+h \right)^{3}}{g R_{e}^{2}}} \qquad \left( \because G \: M_{e} = gR_{e}^{2} \right)$
This is the equation of the time period of revolution of satellite revolving around the earth.
If the satellite revolves very nearly around the earth (i.e $h=0$) then the time period of the satellite from the above equation
$T= 2 \pi \sqrt{ \frac{ \left( R_{e}+0 \right)^{3}}{g R_{e}^{2}}} $
$T= 2 \pi \sqrt{ \frac{ R_{e}}{g}} $
$T= 84.6 \: min $