Distinction between Spontaneous and Stimulated Emission of Radiation

Some of the differences between spontaneous and stimulated emission of radiation are given as follows:

1. In spontaneous emission, an atom in excited state falls to the ground state on its own without any incident photon while in stimulated emission transition takes place by stimulating photons or by an external agency.

2. In stimulated emission for each incident photon there are two outgoing photons in the same direction while in spontaneous emission the emitted photons move randomly in any direction.

3. The photons emitted in spontaneous emiss ion have a random phase and hence are incoherent while in stimulated emission the emitted photons are in phase and hence are coherent.

4. The rate of spontaneous emission is proportional to only the number of atoms in the excited state while the rate of stimulated emission is proportional to the number of atoms left in the excited state as well as on the energy density of the incident radiation.

5. In stimulated emission of radiation an amplified beam is achieved while in spontaneous emission there is no such amplification.

6. The light emitted through the spontaneous emission is not monochromatic while in stimulated transition monochromatic radiation is obtained.

7. Spontaneous emission is not controllable from outside while stimulated emission is controllable from outside.

8. In spontaneous emission, the net intensity is proportional to the number of radiating atoms while in stimulated emission it is proportional to the square of the number of radiation atoms.

Characteristics, Advantages, Disadvantages and Applications of Ruby Laser

Characteristics of Ruby Laser →

Some of the characteristics of ruby laser are given as follows:

1. Ruby laser is the first working laser that was developed in 1960.


2. Ruby lasers are three-level solid-state pulsed lasers with pulse lengths of the order of a millisecond.


3. This laser uses a synthetic Ruby crystal that is Aluminium oxide as its gain medium.


4. A triply ionized chromium $$Cr^{+3} is used as a dopant for active ion, concentration bring of the order of $0.055%$.


5. Ruby crystals are hard and durable, chemically stable and it has good thermal conductivity.


6. Ruby lasers are optically pumped using a flash lamp.


7. In a ruby laser, water or liquid nitrogen is used as a coolant.


8. These lasers produce pulses of visible light at wavelength $6928A^{\circ}$ and $6943A^{\circ}$, with $6943A^{\circ}$ as dominant wavelength which is a deep red color.


9. Ruby laser is highly temperature-dependent.


10. A practical ruby laser operates at about $1%$ efficiency.


11. Pulse repetition rate is comparatively low, of the order of $1$ to $2$ pulse per second.

The Advantages of Ruby Laser →

Some advantages of ruby laser are mentioned below:

1. Ruby laser is very easy to construct and operate.


2. A very strong and intense laser beam up to an output power of $10^{4}- 10^{6} W$, is generated in this laser.


3. It has a degree of coherence.


4. Ruby crystal is hard, durable and it has good thermal conductivity and coherence length.


5. It is chemically very stable.


6. The laser crystal can be grown with a high degree of optical quality.

The disadvantage of Ruby Laser →

Following are some disadvantages of Ruby laser:

1. Ruby cannot be grown in large dimensions.


2. Ruby laser is less directional and has very small efficiency.


3. High excitation energy is required as more than half of the active centers are to be excited to achieve population inversion


4. It has a very small operation for only a few hours.


5. producers pulsed output of microsecond duration($\approx30 \mu s$).


6. Very high heat is produced in these lasers due to which an effective cooling system is required.


7. In these lasers, only a small part of pumping power is utilized in the excitation of chromium ion $Cr^{+3}$ and the rest goes to heat up to apparatus.

Applications of Ruby Laser →

Ruby laser have declined in use with the discovery of a better lasing medium but they are still used in a number of applications some of which are given as follows:

1. These lasers are used in optical holography to produce holographic portraits, in size up to a meter square.


2. These lasers are used in tattoo and hair removal but are being replaced by other lasers.


3. These lasers are used in the measurement of plasma properties such as electron density temperature etc.


4. These lasers are used where short pulses of red light are required.


5. These lasers are used in labs to create holograms of large objects such as aircraft tires to look for weaknesses in the lining.

Spiking in Ruby Laser →

Spiking in Ruby Laser

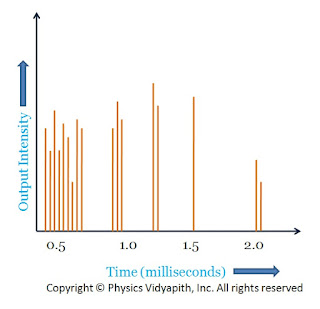
Ruby laser is a three-level pulsed laser. The operation of ruby laser leads to a pulsed output with flash lamps as pumping source. The output of a ruby laser is found to consist of a series of pulses of duration of a microsecond or less. The output of this laser is a highly irregular function of time with the intensity having random amplitude fluctuation of varying duration as shown in the figure. These pulses of the short duration are called spikes and the phenomenon is called laser spiking. Duration of individual spikes is of the order of $0.1-1 \mu s$, the time interval between two adjacent spikes is about $1-10 \mu s$. The power of each spike is of the order of $10^{4}- 10^{5} W$. The characteristic spiking of ruby laser

The Characteristic Spiking of Ruby Laser →

When the pumping source (flash lamp) is turned on the population at the upper level gradually increases while the population at the lower energy level decreases. The duration of the exciting flashlight is of the order of milliseconds and may be sufficiently intense to build up population inversion very rapidly. As soon as the population at the upper level becomes sufficiently large and the threshold condition is reached, laser action starts producing a laser pulse. Due to laser pulsed emission population of upper laser level is depleted more rapidly than it can be restored by flashlight. This process leads to leads to an interruption of laser oscillations, the laser oscillation ceases for a few microseconds. Because the flash lamp is still active it again builds up population inversion and laser oscillations beings causing other spikes and the sequence is repeated. A series of pulses is thus produced itself till the intensity of the flashlight has fallen below the threshold value due to which it is not possible to rebuild the necessary population inversion and the lasing action stops.

Principle, Construction and Working of the Ruby Laser

Principle of Ruby Laser → Ruby laser is the first working laser that was invented by T.H.Maima in 1960. It is a three-level solid-state pulsed laser that uses a synthetic ruby crystal or sapphire$(Al_{2}O_{3})$ as its gain medium and triply ionized chromium$(Cr^{+3})$ is used as a dopant.

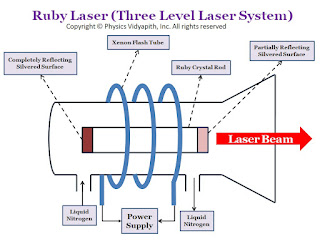
Construction of Ruby Laser → There are the following main components of ruby laser:

1. Active Medium
2. Resonant Cavity
3. Pumping and Cooling Device

Ruby laser diagram

1. Active Medium → The active medium or gained medium in ruby laser is a synthetic ruby crystal or Aluminium oxide $(Al_{2}O_{3})$ in the form of a cylindrical rod having size $2-30cm$ in length and $0.5-2.0cm$ in diameter. The size of the rod main varies depending upon the use. This gain medium falls in the category of 'narrow line width' laser material. A triply ionised chromium $(Cr^{+3})$ is used as doping material or dopant which works as an active ion. For doping of ruby $(Al_{2}O_{3})$, chromium oxide $(Cr_{2}O_{3})$ is mixed as impurity in ruby and small fraction of aluminium ion $(Al^{+3})$ in ruby are replaced by chromium ions $(Cr^{+3})$. The concentration of chromium ions $(Cr^{+3})$ is of the order of $0.055%$ and at this concentration, the number of chromium ions $(Cr^{+3})$ per cubic meter is nearly $10^{25}$. It is the chromium ions $(Cr^{+3})$ that population is set up in ruby laser and gives rise to the laser action. The chromium ions $(Cr^{+3})$ are active centers and provide the energy levels for both lasing transitions and pumping. The host Aluminium oxide $(Al_{2}O_{3})$ itself does not participate directly in lasing action.

2. Resonant Cavity → The ends of the ruby are optically flat and parallel and then silvered, one end completely and the other only partially. The one end of the rod acts as fully reflecting and another one as partially reflecting. The reflectors can be plane-parallel or with a slight curvature, curved mirrors being more useful for compensating the thermal lensing of the rod which takes place during the pumping cycle. The space between the end faces is known as a resonant cavity in which light intensity can be built up or amplified by multiple reflections.

The ends of the ruby rod are polished with great precision, such that the ends are flat to within a quarter of a wavelength of the output light and parallel to each other within a few seconds of arc. The rod with its reflecting ends acts as a Fabry Perot resonator. Modern laser often uses rods with ends cut and polished at "Brewster's Angle" to eliminate the reflections from the ends of the rod.

3. Pumping and cooling Device → In the ruby laser, population inversion is done by optical pumping. Xenon flash lamps provide the most efficient operation of ruby lasers with a pulse duration ranging from milliseconds. The ruby rod is wound by a helical xenon flashlight tube with an excitation source in the form of a power supply. The pumping absorption bands are at $4000 A^{\circ}$ and $5500 A^{\circ}$ with an approximation bandwidth of $500 A^{\circ}$ at each of the wavelengths. Pulses of energies up to $100J$ can be obtained through the pulse repetition rate is comparatively low, of the order of one to two pulses per second which limit the average power. Ruby laser requires high pumping flux to get population inversion due to which a considerable amount of heat is generated during laser operation. Ruby laser being highly temperature-dependent requires an arrangement of effective cooling. Water cooling of the rod combined with the higher thermal conductivity of Ruby provides a sufficient cooling effect to remove the excess heat. For this purpose, water is circulated in a glass tube surrounding the laser system. Being transparent in the wavelength region of pumping bands water does not affect the pumping flux from the flash lamp before it gets absorbed by Ruby road. Liquid nitrogen is also used as a coolant material in ruby lasers.

Working(Lasing Action) of Ruby Laser → The energy level diagram of chromium ion in ruby is shown in the figure below:

The energy level diagram of chromium ion in ruby

The energy level $E_{3}$ has two main pump bands or excited bands $T_{1}$ and $T_{2}$ having a bandwidth of nearly $800A^{\circ}$. The energy level $E_{2}$ which is known as the metastable state in ruby has a double energy level $A_{1}$ and $A_{2}$. These energy levels are separated by nearly $14A^{\circ}$. These are the twofold degenerate energy level.

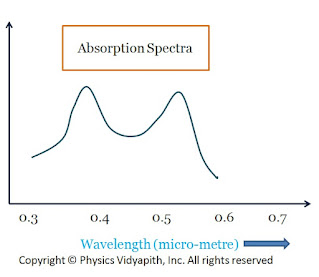
In the normal state, The chromium ions are in-ground energy state $E_{1}$. When light from the flash lamp is made to fall upon the ruby rod the incident radiation is absorbed by chromium ions and rises to an excited state $E_{3}$. The chromium ions in the ground state can absorb a photon of wavelength $5500A^{\circ}$ (green region) and jump to energy band $T_{2}$. It can also absorb the photon of a wavelength $4000A^{\circ}$ (Blue region) and jump to energy band $T_{1}$. The absorption spectrum of chromium ions is shown in the figure below

Absorption Spectra

The chromium ion goes to upper energy state $T_{1}$and $T_{2}$ and stay for $10^{-8} sec $ and then make non radiative transition to metastable states $E_{1}$ and $E_{2}$ respectively which have very log life time $\approx10^{-3}sec$. The number of atoms in these states keeps increasing and at the same time number of atoms in the ground state $E_{1}$ goes on decreasing due to optical pumping. Thus the population inversion is achieved between the metastable state and ground state. At room temperature, if radiation is kept constantly, during the process of pumping, the population at $A_{2}$ level is almost $15%$ more than at level $A_{1}$. Some of the excited atoms in states $E_{3}$ return to ground state $E_{1}$ but with less probability.

When the population inversion is achieved light amplification starts in the resonant cavity. When excited atoms at metastable state $E_{2}$ make transition to ground level $E_{1}$ there are two weak lines at $6943 A^{\circ}$ ($A_{2}$ → $E_{1}$) and $6928 A^{\circ}$ ($A_{1}$ → $E_{1}$) each of width $\approx 6 A^{\circ}$. But Under the lasing condition, the line $6943 A^{\circ}$ dominates over $6928 A^{\circ}$. The emission spectrum of chromium ions in ruby is shown in the figure below:

Emission Spectra

It shows that pumping transitions are spectrally broad while the emission transition is narrow. The wavelength of two spectral lines $6943 A^{\circ}$ and $6928 A^{\circ}$ are temperature dependent.

Four Level Pumping in Laser

Description:

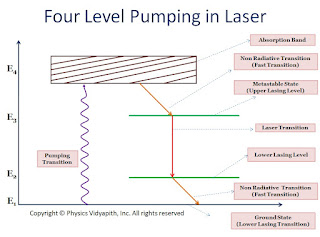
In four-level pumping, atoms of ground energy state go to upper energy state$(E_{4})$ by pumping transition to achieve the population inversion. Due to the short time of the upper energy state atoms go to metastable state by nonradiative transitions or spontaneous emission. Atoms of metastable state come to lower lasing level by laser transition process. The atoms come from lower lasing level to ground state by nonradiative transition or spontaneous emission. This process is repeated continuously.

Four-level pumping in Laser

In contrast to level pumping, the lower lasing transition level in the four-level scheme is not the ground state and is virtually vacant. As soon as some atoms are pumped to the upper lasing level, population inversion is achieved. So it is required less pumping energy than a three-level laser system. this is the major disadvantage of this scheme. Further, the lifetime of the lower lasing level is shorter as it is not a metastable state. Hence atom in level $E_{2}$ quickly drops to the ground state. This depletion of the $E_{2}$ energy level helps sustain the population inversion by avoiding and accumulation of atoms in the lower lasing level. Therefore four-level laser system can operate in a continuous wave mode.

Three level pumping in Laser

Description:

Three-level pumping in laser is suitable for attending population inversion.

When atoms of ground energy state observe the photon from incident energy. It goes from lower energy or ground energy state two to a higher energy state but the lifetime of a high energy state is very short that is $10^{-8}$ $sec$ i.e. So an atom cannot stay for a long time in high energy state i.e.$E_{3}$ and then the atom goes for non-radiative transition and reach to the metastable state. In a metastable state, Atoms cannot go to a lower energy state or ground energy state directly. Therefore, These atoms come from a metastable state to a lower energy state or ground energy state by lasing transition.

Three-level pumping in Laser

This is the process of three-level pumping in a laser. For better pumping efficiency, The level $E_{3}$ should be the band of energy levels instead of being a single arrow line. It allows the use of pumping radiation of wider bandwidth to excite more atoms. However, the major disadvantage of the three-level scheme is that it requires very high pumping powers. The three-level laser system can produce light only in pulses. Once stimulated emission commences, the metastable state $E_{2}$ gets depopulated very rapidly and the population of the ground energy state increases quickly. As a result, the population inversion ends. One has to wait till population inversion is again established. Thus, the Three-level laser system operates in pulse mode.

Two Level Pumping in Laser

Two-level pumping occurs between two energy levels. All the process of laser (absorption, spontaneous emission, or stimulated emission) occurs between two energy level. The absorption of light or emission of light energy is the difference between two energy levels. If two energy levels are $E_{1}$ and $E_{2}$ so absorption or emission of a photon →

$E_{2}-E_{1}=h\nu$

Where$h$ → Planck's Constant$\nu$ → Frequency of photon

Two-level pumping in laser is not suitable for attaining the population inversion. The transition of atoms between two energy levels by stimulated emission is called a lasing transition. The lower level is known as the lower lasing level and the upper level is known as the upper lasing level. The upper lasing level must be a metastable level. The uppermost level to which atoms are in the excited state is known as the pumping level. The transition between the ground level and pumping level is called the pumping transition.

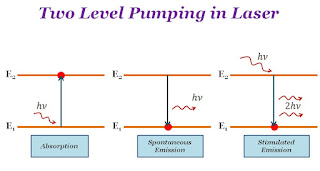Two-level pumping Laser

Absorption, Spontaneous Emission and Stimulated Emission of Radiation

Absorption →

When a photon (or light) incident on atoms then atoms absorb the energy from the photon and jump from a lower energy state to a higher energy state. This transition is known as induced absorption or stimulated absorption or simply as absorption.

The process is represented as

$A+h\nu=A^{*}$

Where$A$ → Lower energy state atom$A^{*}$ → Excited or Higher energy state atom

Absorption Transition

If $N_{1}$ and $N_{2}$ is the population of energy $E_{1}$ and $E_{2}$, the number of atoms per unit volume that makes upward transitions from the lower levels to the upper level per second is called the rate of absorption transitions. It is represented by

$R_{abs}=-\frac{dN_{1}}{dt} \qquad(1)$

Where $-\frac{dN_{1}}{dt}$ is rate of decrease of population at the lower energy level $E_{1}$

The rate of absorption transition can also be represented by the rate of the increase of population at the upper energy level $E_{2}$. i.e

$R_{abs}=\frac{dN_{2}}{dt} \qquad(2)$

From equation $(1)$ and equation $(2)$

$R_{abs}=-\frac{dN_{1}}{dt} =\frac{dN_{2}}{dt} \qquad(3)$

The number of absorption transitions occurring within the material at any instant will be proportional to the population in the lower energy level and the number of photons per unit volume in the incident beam. The rate of absorption can be expressed conveniently.

$R_{abs}=B_{12} \rho(v) N_{1} \qquad(4)$

Where$\rho(v)$ → Energy density of incident light$B_{12}$ → Einstien coefficient for induced absorption and it indicates the probability of an induced transition from level 1→2.

At thermal equilibrium, the population in the lower energy state is much larger than that in the higher energy state. Therefore, as light propagates through the medium. These lower energy state atoms gets absorbed.

Spontaneous Emission →

When atoms absorb energy from photons, it goes from lower energy levels to higher energy levels. An excited atom stays at the excited energy level for an average lifetime $\tau_{sp}$. If it is not stimulated by any other agent during its short lifetime, the excited atom undergoes a transition to the lower energy level on its own and gives up the excess energy in the form of a photon. This process is called spontaneous emission.

The process in which an excited atom emits a photon all by itself and without any external impetus is known as spontaneous emission.

The process is represented as

$A^{*} → A+ h \nu \qquad(5)$

Spontaneous Emission Transition

The rate of spontaneous transition $R_{sp}$ is given by

$R_{sp}=-\frac{dN_{2}}{dt}= \frac{N_{2}}{\tau_{sp}} \qquad(6)$

The number of emitted photons will be proportional to the population of the excited energy state only and can be expressed as follows

$R_{sp}=A_{21}N_{2}\qquad(7)$

Where $A_{21}$ is known as the Einstein coefficient for spontaneous emission and is a function of frequency and properties of the material. It indicates the probability of spontaneous emission is independent of light energy.

From equation$(6)$ and equation$(7)$

$A_{21}=\frac{1}{\tau_{sp}} \qquad(8)$

Important features of spontaneous emission →

1. The process of spontaneous emission isn't amenable for control from outside.


2. It is essentially probabilistic in nature.


3. The light isn't monochromatic due to various line broadening processes.


4. Due to a lack of directionality, the light spreads in all directions around the source. The intensity of light decreases as the distance from the source increases.


5. The light is incoherent.


6. An atom can radiate into any of the $4\pi$ steradians with any sense of polarization.

Stimulated Emission →

An atom absorbs the energy of a photon, goes from a lower energy level to a high energy level(or excited level). If a photon with appropriate energy interacts with the excited atom, it can trigger the atom to undergo a transition to the lower level and emit another photon. This process is known as stimulated emission.

The process of emission of a photon by an excited state atom through a forced transition occurring under the influence of an external agent is called induced or stimulated emission. The process may be represented as

$A^{*}+h\nu → A+2h\nu \qquad(9)$

Stimulated Emission Transition

The rate of stimulated emission of photons is given as by

$R_{st}=B_{21}\rho(v)N_{2} \qquad(10)$

Where $B_{21}$ is Einstein coefficient for stimulated emission

Important features of spontaneous emission →

1. The process of stimulated emission is controlled from the outside.


2. The photon emitted in this process propagates in the same direction as that of the stimulated photon.


3. The emitted photon has exactly the same frequency, phase, and plane of polarization as the incident photon.


4. The light produced in the process is directional, coherence and monochromatics.

Einstein Coefficient Relation

Derivation of Einstein Coefficient Relation→ Let us consider the $N_{1}$ and $N_{2}$ is the mean population of lower energy state and upper energy state respectively. If the energy density of incident light is $\rho(\nu)$ then

The rate of transition of number of atoms due to absorption process:

$R_{abs}=B_{12} \: \rho(v) \: N_{1} \qquad(1)$

The above equation shows the number of atoms absorbing the photon per second per unit volume

Where $B_{12}$= Einstein Absorption Coefficent

The rate of transition of number of atoms due to sponteneous emission process:

$R_{sp}=A_{21} \: N_{2} \qquad(2)$

The above equation shows the number of atoms emitting the photon per second per unit volume due to spontaneous emission

Where $A_{21}$= Einstein Spontaneous Emission Coefficient

The rate of transition of the number of atoms due to stimulated emission process:

$R_{st}=B_{21} \: \rho(v) \: N_{2} \qquad(3)$

The above equation shows the number of atoms emitting the photon per second per unit volume due to stimulated emission

Where $B_{21}$= Einstein Stimulated Emission Coefficient

Under the thermal equilibrium, the mean population $N_{1}$ and $N_{2}$ in lower and upper energy states respectively must remain constant. This condition requires that the transition of the number of atoms from $E_{2}$ to $E_{1}$ must be equal to the transition of the number of atoms from $E_{1}$ to $E_{2}$. Thus

$\left.\begin{matrix}The \: number \: of \: atoms \: absorbing \\ photons \: per \: second \: per \: unit \: volume \end{matrix}\right\} = \left.\begin{matrix} The \: number \: of \: atoms \: emitting \\ photons \: per \: second \: per \: unit \: volume \end{matrix}\right\}$

i.e $R_{abs}= R_{sp}+R_{st}$

$B_{12} \: \rho(v) \: N_{1}= A_{21} \: N_{2} + B_{21} \: \rho(v) \: N_{2}$

$B_{12} \: \rho(v) \: N_{1} - B_{21} \: \rho(v) \: N_{2} = A_{21} \: N_{2} $

$ \rho(v) (B_{12} \: N_{1} - B_{21} \: N_{2} ) = A_{21} \: N_{2} $

$\rho(v)=\frac{A_{21} \: N_{2}}{(B_{12} \: N_{1} - B_{21} \: N_{2} )} \qquad(4)$

We know that

$\frac{N_{1}}{N_{2}}=e^{\frac{(E_{2}-E_{1})}{kT}}$

$\frac{N_{1}}{N_{2}}=e^{\frac{h\nu}{kT}}$

Now substitute the value of $\frac{N_{1}}{N_{2}}$ in equation $(4)$

$\rho(v)=\frac{A_{21}}{B_{12}} \left [ \frac{1}{e^{\frac{h\nu}{kT}}- \frac{B_{21}}{B_{12}}} \right ] \qquad(5)$

According to Planck's Radiation Law

$\rho(v)=\frac{8\pi h \nu^{3}}{c^{3}} \left [ \frac{1}{e^{\frac{h\nu}{kT}}- 1} \right ] \qquad(6)$

Now comparing the equation $(5)$ and equation $(6)$

$\frac{B_{21}}{B_{12}}=1$ and $\frac{A_{21}}{B_{12}}=\frac{8\pi h \nu^{3}}{c^{3}}$

From the above equation, we get

$B_{21}=B_{12}$

$B_{12}=B_{21}=\frac{c^{3}}{8\pi h \nu^{3}}A_{21}$

Laser and properties of a Laser beam

Laser→

LASER is an acronym for Light Amplification by Stimulated Emission of Radiation. It is a device that produces a highly intense monochromatic, collimated, and highly coherent light beam. Laser action mainly depends on the phenomenon of population inversion and stimulated emission.

The first successful Laser is a solid-state laser which was built by TH Maiman in 1960 using Ruby as an active medium.

Note→

The laser has often been referred to as an optical MASER because it operates in the visible spectrum portion of the spectrum. In general, when the variation occurs below the infrared portion of the electromagnetic spectrum, the term MASER will be employed, and when stimulated emission occurs in the infrared, visible, or ultraviolet portion of the spectrum the term laser or optical MASER will be used.

Properties of a Laser Beam→

The laser beam has the following main characteristics properties:

1. A laser beam has high directionality and can be emitted only in one direction. The divergence of the laser beam can be less than $10^{-5}$ radian. Due to high directionality, these beams can be focused in very small areas.


2. A laser beam is very narrow and hence can travel long distances without any spread. The spectral width ($\Delta \lambda$)of a laser beam is of the order of $10^{-6} A^{\circ}$.


3. A laser beam is highly monochromatic. Its monochromaticity is much more than that of any conventional monochromatic source.


4. The laser beam has high intensity and high power levels that can produce a temperature of the order of $10^{4} \: ^{\circ}C$.


5. A laser beam has a high degree of coherence. It is highly temporally and spatially coherent.

Difference between stable and unstable resonators

Difference between Stable and Unstable Resonators:

1. The oscillating beam is converged in stable resonator while in unstable resonator is spreads out of the the resonator.


2. In stable resonator laser output is from the centre of optical axis while in unstable resonator laser output comes from the edge of the output mirror.


3. The field is confined to the axis in stable resonator while it is not so in unstable resonator.


4. Stable resonators are used for low power lasers while unstable resonators are used for high power lasers.


5. In stable resonator these remains risk of breakage of the m  irrors while it is reduced to unstable resonators.


6. The mode volume is is small in stable resonators while it is large in unstable resonators.


7. The geometrical losses are large in unstable resonator in comparison to stable resonators.


8. In unstable resonators better beam quality may be achieved in comparison to stable resonators.

Applications of Lasers

Description of Application of Lasers:

There are widespread applications of lasers in various disciplines such as in medicine, industries, astronomy, communication, chemistry, etc. Some of the laser applications are given below in short:

1.) Lasers in Medicine:Some of the applications of lasers in the medical are such as in:

• Controlling haemorrhage.
• Treatment of the liver and lungs and for the elimination of moles and tumours developing on the skin tissues.
• Therapy and stomatology.
• Microsurgery for virtually painless treatment.
• Ophthalmology to reattach a detached retina.
• Penetration of blood vessels in the eye for treating glaucoma.
• Treatment of cancer.
• Dentistry etc.

2.) Lasers in Industries: Some of the industrial applications of lasers are as follows:

• Testing the quality of optical components such as lenses, prism, gratings etc.
• More accurate measurement of the sizes of physical quantities, precision length measurement.
• Gelling of extremely fine holes in various substances, such as in paper clips, teeth, diamonds, human hair, etc.
• Cutting of different types of hard materials.
• Technical motion picture photography.
• Detection of fingerprints.
• High-power laser eyes are useful in welding small metal points, such as in the field of electronics and microelectronics thermocouple welding to a substrate etc.
• Used in vaporizing materials for subsequent deposition on a substrate.
• Rock-crushing and boring tunnels.

3.) Lasers in astronomy: Lasers are useful in radio telescopes to exchange and extend their range of observation and in amplification of very faint radio signals from space. The application of lasers is to record the burst of light and radiation waves from stars etc.

4.) Atmospheric Optics: Lasers are used for remote probing of the atmosphere including, the measurement of traces of pollutant gases, temperature, water, vapour concentration etc. Laser radar provides the distribution of atmospheric pollutants in different vertical sections.

5.) Lasers in Biology: Lasers are useful in micro Raman spectroscopic analysis for biological and biomedical samples available only in very small quantities. Argon-ion Laser is used to obtaining scattering spectra of a wide range of biological materials.

6.) Laser in Ranging: Lasers are used in finding the accurate position of a distant object and also make it possible to determine the size and shape of your object and its orientation. Lasers are useful in the measurement of the velocity of moving objects. Laser fluouresensors are used to monitor remote environments.

7.) Lasers in Communication: Lasers are very useful in transmitting a large volume of signals over long distances. The communication capacity of typical light is about 10⁶ greater than that of typical microwaves. Due to the fact that optical frequencies are extremely large as compared to conventional radio waves and microwaves, a light beam acting as a carrier wave can carry more information in comparison to radio waves and microwaves. Lasers are thus more efficient in long-distance communication. Due to the coherence and monochromaticity of laser beams, these are used in signal modulation. Glass fibres are used for the transmission of light waves employing the principle of total internal reflection. Laser is useful in communication with earth satellites, in rocketry, etc.

8.) Lasers in Chemistry: Lasers are used in chemistry in different ways such as in:

• Isotope separation for the enrichment of Uranium reactor fuel.
• The study of the nature of chemical bonds.
• Trace analysis of gases.
• Detection of the small number of atoms produced by the interaction of low-energy solar neutrinos.
• Microelectronic designing and fabrication.
• Triggering chemical and photochemical reactions
• Information regarding the presence of a trace of metals in various tissues etc.
• Thermo nuclear fusion reactor.

9.) Lasers in spatial frequency filtering: lasers are used in:

• Contrast enhancement of the image.
• Detecting random error in a periodic structure.
• Character recognition problems in an optical image forest of character recognition problems are used in military defence to identify certain objects of interest.
• Removing the dot patterns of the images.

10.) Lasers in Holography: Although the principle of holography was laid down by Gabor in 1948, but holography attend practical importance after the development of the laser in 1960. Due to high monochromaticity and spatial coherence properties lasers are used in holography. Holography is a method of recording information from a three-dimensional object in such a way that a three-dimensional image may subsequently be reconstructed. In holography, the photographic plate for holograms is illuminated by two laser beams simultaneously, one carrier beam and the other object beam. The hologram contains the detail of both the amplitude and phase of light received from different parts of the three-dimensional object. The holographic technique using a laser beam can be used for the examination of complicated shapes with diffusely reflecting surfaces which is not possible when ordinary light sources are used. The computer memories using laser as a source have very high storage capacity (~10¹⁰ bits/mm³) with rapid access and are easy to align and less subject to problems of vibration than other optical memories. A holographic memory records and read out a large number of bits simultaneously.

11.) Lasers in the Military: Lasers are useful in various military applications such as:

• Range finders, forget accurate information about the range to improve the first hit probability.
• Beam rider, for the guidance of weapons by making the weapon remain within the beams, All the way to get the target.
• Simulators simulate all aspects of the firing situation to ensure that the enemy is destroyed.
• In communication with submarines or satellites.
• Use again cruise missiles towards a ship etc.