Generation of wave function for a free particle

Simple harmonic motion:

If an object repeats the process or path at a fixed interval of time is known as periodic motion or Uniform circular motion. It is also called the Simple harmonic motion.

We know that the wave is the study of infinite S.H.M.

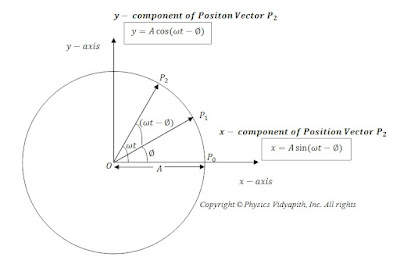
Let us consider a particle is moving with uniform velocity in a circular path with radius $A$ i.e. particle is doing simple harmonic motion. Let at any instant $t$ particle move from position $P_{1}$ to $P_{2}$. So vector resolution of $P_{2}$ position is:

From below figure-

Horizontal Component i.e. $x$ component of position vector $P_{2}$:

$x=A sin(\omega t - \phi) \qquad (1)$

Vertical Component i.e. $y$ component of position vector $P_{2}$:

$y=A cos (\omega t - \phi) \qquad (2)$

Simple harmonic motion of a particle

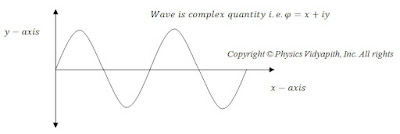
According to Max Born hypothesis-

“Wave is a complex quantity which is represented by a wave function $\varphi$ ”

 i.e. wave function mathematically can be represented as

$\varphi= x+iy \qquad (3)$

Substitute the value of $x$ component and $y$ component in above equation-

$\varphi= A sin (\omega t - \phi)+ i A cos (\omega t - \phi) $

$\varphi=A [sin (\omega t - \phi)+ i cos (\omega t - \phi) ]$

$\varphi=A e^ {i(\omega t - \phi)} \qquad (4)$

Where $\phi$is the phase of the wave. The value of $\phi$ can be found by the relation between phase difference and path difference of wave plane progressive wave.

$\phi =\frac {2\pi}{\lambda}\cdot x$

$\phi = k\cdot x$

Now substitute the value of $\phi$ from above in equation $(4)$. So wave function equation can be written as-

$\varphi=A e^ {i(\omega t - k \cdot x)}$

Propagation of a wave along the x-axis

Let a particle of mass m be in motion along the positive x-direction with accurately known momentum $p$ and total energy $E$.

So from the equation of plane progressive wave-

$\psi(x,t)=Ae^{-i\omega (t-\frac{x}{v})} \qquad(5) $

$\psi(x,t )=Ae^{-i(\omega t-kx)}$

$\psi(x,t )=Ae^{i(kx-\omega t)} \qquad(6)$

According to Planck’s hypothesis-

$E=h\nu  \qquad(7) $

$E=\frac{h}{2 \pi }\cdot 2 \pi \nu$

$E=\hbar.\omega$

$\omega=\frac{E}{\hbar } \qquad(8)$

According to de Broglie hypothesis-

$\lambda= \frac{h}{p}$

$p =\frac{h}{\lambda }$

$p =\frac{h}{2 \pi }\cdot \frac{2 \pi}{\lambda}$

$p=\hbar\cdot k$

$k=\frac{p}{\hbar}\qquad(9)$

Now put the value of $\omega$ and $k$ from equation $(8)$  and equation $(9)$in equation$(6)$

$\psi (x,t)=Ae^{ i(\frac{p}{\hbar }x-\frac{E}{\hbar }t)}$

$\psi (x,t )=Ae^{\frac{i}{\hbar}(px-Et)}$

The three-dimensional equation of wave function of a free particle:

$\psi (\overrightarrow{r},t)=Ae^{\frac{i}{\hbar}(\overrightarrow{p}x-Et)}$