Posts
Showing posts from August, 2022

Posted by
Physics Vidyapith
Magnetic dipole moment of a revolving electron
- Get link
- Other Apps
Posted by
Physics Vidyapith
Magnetic potential energy of current-loop in a magnetic field
- Get link
- Other Apps
Posted by
Physics Vidyapith
Magnetic Dipole Moment of Current carrying loop
- Get link
- Other Apps
Posted by
Physics Vidyapith
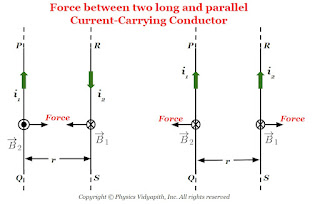
Force between two long and parallel current-carrying conductor
- Get link
- Other Apps
Posted by
Physics Vidyapith
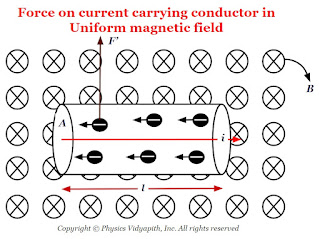
Force on current carrying conductor in uniform magnetic field
- Get link
- Other Apps