Conversion of Galvanometer into an Ammeter

What is Ammeter?

An Ammeter is an instrument that is used to measure the electric current in the electric circuits directly in Ampere. The instrument which measures the current of the order of milliampere $(mA)$ is called the milliammeter. The internal resistance of the ideal ammeter is always zero.

What is Galvanometer?

The galvanometer is an instrument that is used to measure the very small amount of the electric charge passing through the circuit. The internal resistance of the Galvanometer is not zero.

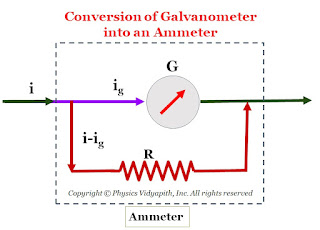
Galvanometer used as Ammeter: To use the galvanometer as an ammeter in the circuit, The resistance of the galvanometer should be very small or almost zero as compared to the other resistance of the circuit. Because the internal resistance of an ideal ammeter is zero.

So a low resistance is connected in parallel to the galvanometer which is known as a shunt.

When a low resistance is connected in parallel to the galvanometer then the resultant resistance decreases as compared to the other resistance of the circuit and it can be easily used as an ammeter and the actual current can be measured through it.

Mathematical Analysis:

Let us consider, $G$ is the resistance of the coil of the galvanometer and the $i_{g}$ current, passing through it, produces full scale deflection. If $i$ is the maximum current of the circuit then a part of current $i_{g}$ passes through the galvanometer and the remaining current $(i-i_{g})$ passes through the shunt $S$. Since $S$ and $G$ are parallel, the potential difference across them will be the same:

$i_{g} \times G = \left( i- i_{g} \right) \times S \qquad(1)$

$\frac{i_{g}}{i}=\frac{S}{S+G}$

i.e. only $\frac{S}{S+G}$th part of the total current will flow in the coil of the Galvanometer. Again from equation $(1)$:

$S=\left(\frac{i_{g}}{i-i_{g}}\right)G \qquad(2)$

If the current $i_{g}$ passes through the coil of the galvanometer and produces a full-scale deflection on the meter scale of a galvanometer, then the current $i$ in the circuit corresponds to the full-scale deflection. Thus, with a shunt $S$ of the above value, the galvanometer will be an ammeter in the range $0$ to $i$ ampere.

Example: Let a current of $1 A$ in the coil of a galvanometer produce a full-scale deflection. To convert it into an ammeter of range $10A$, a shunt is required such that when the current in the circuit is $10A$, only $1A$ flows in the coil remaining passes through the shunt. Now From substitute the $i_{g}=1A$ and $i=10A$ in the above equation $(2)$:

$\frac{S}{G}= \frac{1}{\left( 10 -1 \right)}$

$\frac{S}{G}= \frac{1}{9}$

The resistance of the shunt should be only $\frac{1}{9}$th the resistance of the galvanometer coil.

Note: As the shunt resistance value is very small so the combined resistance of the galvanometer and the shunt also becomes very small and hence the ammeter has a much smaller resistance than the galvanometer.

Resistance of Ammeter:

$\frac{1}{R_{A}}=\frac{1}{G}+\frac{1}{S}$

$R=\frac{G\:S}{G+S}$

When a Galvanometer is used in the circuit and connected in the series to measure the electric current:

The galvanometer is used in series to measure the electric current of the circuit so that the whole amount of the current passes through it. but the galvanometer will have some resistance due to the resultant resistance of the circuit increasing and the current in the circuit somewhat decreasing. Therefore the current read by the Galvanometer is less than the actual current.