Newton's Rings:
Experimental Arrangement:
A plano-convex lens $l_{1}$ of large radius of curvature is placed on a plane glass plate $G_{1}$ with the curved surface touching the glass plate.
An air film is enclosed between the curved surface of the lens and the glass plate.
A sodium vapor lamp $S$ is kept at the focus of a biconvex lens $L$ which converts the diverging beam of light into a parallel beam. The parallel beam of light is made to fall on a glass plate $G_{2}$ kept at an angle of $45^{\circ}$ with the incident beam.
A part of incident light is reflected toward the plano-convex lens. This light is again reflected back, partially from the top and partially from the bottom of the air fil and transmitted by the glass plate $G_{2}$. The interference of these rays is observed through a microscope $M$.
 |
| Newtons Rings Experiment Setup-Ray Diagram |
Explanation of the formation of Newton's rings:
Division of amplitude takes place at the curved surface of the plano-convex lens.
The incident light is partially reflected and partially transmitted at the curved surface.
The transmitted ray is reflected from the glass plate. These two rays interfere in reflected light
The path difference between these rays depends on the thickness of the air film enclosed between the curved surfaces of the lens and glass plate which increases radially outward from the center. The thickness of the air film is zero at the center
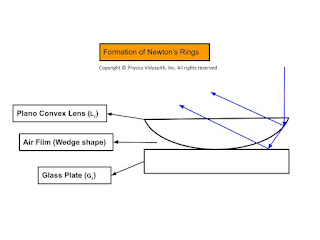 |
| Formation of Newton Rings |
Path difference:
Let $t$ is the thickness of air film at a radial distance of $r$ and $R$ is the radius of curvature. So the path difference for a wedge-shaped film is
$\Delta=2 \mu t \: cos(r+\alpha) \pm \frac{\lambda}{2} \qquad(1)$
HereRefractive index of air film ($\mu)=1$$\alpha$ is very small i.e. $\alpha \approx 0$For normal incidence $r=0$ i.e $cos(\alpha+r)=1$
Now apply the above condition to equation $(1)$ then we get
$\Delta = 2t + \frac{\lambda}{2} \qquad(2)$
 |
| Newton’s Rings Diagram for Path difference Formula Calculation |
Form figure, In $\Delta OAB$, apply the Pythagoras theorem
$OB^{2}=OA^{2}+AB^{2}$
$R^{2}=(R-t)^{2}+r^{2}$
$R^{2}=R^{2}+t^{2}-2Rt+r^{2}$
$2Rt=t^{2}+r^{2}$
As $t$ is very small, $t^{2}$ can be neglected in comparison with $r^{2}$. So
$2Rt=r^{2}$
$2t=\frac{r^{2}}{R} \qquad(3)$
Here $r$- Radius of a circle for which thickness is $t$
If $D$ is the diameter of this circle then
$r=\frac{D}{2}$
So from equation $(3)$
$2t=\frac{D^{2}}{4R} \qquad(4)$
Substitute the value of $2t$ in equation $(2)$ then we get
$\Delta = \frac{D^{2}}{4R}+\frac{\lambda}{2}$
Diameter of Bright rings:
For bright rings, the condition for constructive interference is satisfied. i.e.
$\Delta =n \lambda$
So from the above equations, we get
$\frac{D^{2}}{4R}+\frac{\lambda}{2}=n \lambda $
Where $D_{n}$- Diameter of the $n^{th}$ bright ring
$\frac{D^{2}}{4R}=(2n-1) \frac{\lambda}{2}$
$D_{n}= \sqrt {2 \lambda R (2n-1)}$
Where $n=1,2,3,4........$
$D_{n} \propto \sqrt{(2n-1)}$
i.e The diameter of the bright rings are proportional to the square root of odd natural numbers.
Diameter of Dark ring:
Condition for destructive interference is satisfied for dark rings i.e.
$\Delta=(2n+1)\frac{\lambda}{2}$
$\frac{D^{2}}{4R}+\frac{\lambda}{2}=(2n+1)\frac{\lambda}{2}$
$\frac{D^{2}}{4R}+\frac{\lambda}{2}=n \lambda + \frac{\lambda}{2}$
$\frac{D^{2}}{4R}=n \lambda$
$D_{n}= \sqrt{4Rn\lambda}$
$D_{n} \propto \sqrt{n}$
Where $n=1,2,3,4........$
i.e The diameter of dark rings are proportional to square root of natural numbers.





