Resolving power of an optical instrument:
The ability of an optical instrument to just resolve the images of two closely spaced objects is called its resolving power.
Limit of Resolution:
The smallest distance between two closely spaced objects that can be seen as separated or just separated from each other through an optical instrument is known as the limit of resolution of that optical instrument.
Rayleigh Criterion:
Rayleigh criterion describes the separation between the two objects or wavelengths (i.e. resolving power) by the resultant intensity distribution of objects and wavelengths. According to Rayleigh's criterion, there are the following cases:
Case:1 If two point sources have very small angular separation, then central or principal maxima in their diffraction patterns will overlap to a large extent and resultant intensity shows uniform variation. As shown in the figure below. In this case, the two objects or wavelengths can not be distinguished or unresolved.
Case:2 If two point sources have very large angular separation then the central or principal maxima are widely separated and the resultant intensity shows two widely separated peaks. As shown in the figure below. In this case, the objects or wavelengths are resolved well.
Case:3 If the central or principal maxima in the diffraction pattern of one object or wavelength coincide with the first minima in the diffraction pattern of the other objects or wavelength then the resultant intensity shows a small dip. As shown in the figure below. In this case, the objects or wavelengths are seen to be just separate or just resolved.
Showing posts with label Optics. Show all posts
Showing posts with label Optics. Show all posts
Principle Construction, Working and Angular Magnification of Simple Microscope
Principle of Simple Microscope:
The principle of the simple microscope is based on the magnification of an image by using a simple convex lens.
Construction:
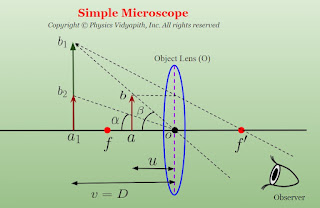
A simple microscope consists of one convergent lens only. The object is placed between the lens and its focal length, and the eye is placed just behind the lens. Then the eye sees a magnified, erect, and virtual image on the same side as the object at the least distance of distinct vision $(D)$ from the eye, and the image is then seen most distinctly.
Working:
If the small object $ab$ is placed between a lens $O$ and its first focus $f$ then Its magnified virtual image $a_{1}b_{1}$ is formed at a distance $D$ from the lens. Since the eye is just behind the lens, the distance of image $a_{1}b_{1}$ from the eye is also $D$.
Angular Magnification Or Magnifying Power($M$):
The ratio of the angle subtended by the image at the eye ($\beta$) to the angle subtended by the object at the eye when placed at the least distance of distinct vision ($\alpha$) is called the angular magnification or magnifying power.
$M= \frac{Angle \: subtended \: by \: the \: image \: at \: the \: eye \: (\beta)}{Angle \: subtended \: by \: the \: object \: at \: the \: eye \: when \\ placed \: at \: least \: distance \: of \: distinct \: vision \: (\alpha)}$
$M=\frac{\beta}{\alpha} \approx \frac{tan \beta}{tan \alpha} \quad (1)$
From figure
$tan \beta = \frac{ab}{oa} $
$tan \alpha = \frac{a_{1}b_{2}}{a_{1}o}$
Here $a_{1}b_{2} = ab$
$tan \alpha = \frac{ab}{a_{1}o}$
Now substitute these values in equation $(1)$, then
$M=\frac{\frac{ab}{ao}}{\frac{ab}{a_{1}o}}$
$M=\frac{a_{1}o}{ao}$
Here $ao = u$ (Distance between object and optical center of the lens) and $a_{1}o = D$ (Least Distance of distinct vision), then the above equation can be written as
$M=\frac{D}{u} \qquad(2)$
We know that the lens formula $\frac{1}{v}-\frac{1}{u} = \frac{1}{f}$
Now put
$v=-D$ (The image $a'b'$ is being formed at a distance $D$ from lens)
$u=-u$
$\frac{1}{-D}-\frac{1}{-u} = \frac{1}{f}$
Multiply $D$ in the above equation
$-\frac{D}{D}-\frac{D}{-u} = \frac{D}{f}$
$-1-\frac{D}{-u} = \frac{D}{f}$
$\frac{D}{u} =1 + \frac{D}{f} \qquad(3)$
From equation $(2)$ and equation $(3)$, then
$M=1 + \frac{D}{f} $
If eye is kept at distance $d$ from lens then $v=-(D-d)$, and the magnifying power will be
$M=1+\frac{D-d}{f}$
To see with a relaxed eye, the image $a'b'$ should be formed at infinity. In this case, the object $ab$ will be at the focus of the lens, i.e. $u=f$ then magnifying power
$M= \frac{D}{f} $
$v=-D$ (The image $a'b'$ is being formed at a distance $D$ from lens)
$u=-u$
Light and its properties
The basic definition of Light:
Light is a form of energy that produces the sensation of vision in the eye by which we can see objects.
There are some facts about light as follows:
1. Lightwave moves along a straight line path.
2. Light waves can travel through both a vacuum and a medium.
3. Light is an electromagnetic wave.
4. Light waves are transverse waves in nature.
5. Light can be dispersed.
Besides these facts, light also shows the phenomenon of interference, diffraction, polarisation, photoelectric effect, etc.
To explain the above facts, many principles have been given from time to time, e.g., Newton's corpuscular theory, Huygen's wave theory, Maxwell's principle of electromagnetic waves, Planck's quantum principle, dual nature of light, etc.
Principle Construction, Working and Angular Magnification of Compound Microscope
Principle: The principle of the compound microscope is based on the magnification of an image by using two lenses.
Construction: A compound microscope consists of two convergent lenses (i.e. objective lens $O$ and eye-piece lens $e$) placed coaxially in a double tube system. The objective lens is an achromatic convergent lens system of short focal length and short aperture. The other eye-piece lens $e$ is also an achromatic convergent lens system of large focal length and large aperture. The observation is taken through the eye-piece lens by the observer. The eye-piece lens is fitted outer side of a movable tube and the inner side connects with a non-movable tube in which the objective lens is fitted on another side of the non-movable tube. The separation between the objective or eye-piece lens can be changed by an arrangement, this is known as rack and pinion arrangement.
Working: Suppose a small object $ab$ is placed slightly away from the first focus $f_{\circ}$ of the objective lens which forms a real, inverted, and magnified image $a_{1}b_{1}$. Now adjust the eye-piece lens by moving like this, that the image $a_{1}b_{1}$ lies in between the optical center and the second focal length $f_{e}$ of the eye-piece lens. This image $a_{1}b_{1}$ works as an object for the eye-piece lens which forms a magnified, virtual, and final image $a_{2}b_{2}$. The final image $a_{2}b_{2}$ is generally formed at the least distance $D$ of distinct vision, although it can be formed anywhere between this position and infinity.
Angular Magnification Or Magnifying Power($M$):
The angular magnification or magnifying power can be defined as the ratio of the angle subtended by the image at the eye ($\beta$) to the angle subtended by the object at the eye when placed at least distance of distinct vision ($\alpha$)
$M= \frac{Angle \: subtended \: by \: the \: image \: at \: the \: eye \: (\beta)}{Angle \: subtended \: by \: the \: object \: at \: the \: eye \: when \\ placed \: at \: least \: distance \: of \: distinct \: vision \: (\alpha)}$
$M=\frac{\beta}{\alpha} \approx \frac{tan \beta}{tan \alpha} \quad (1)$
From figure
$tan \beta = \frac{a_{2}b_{2}}{a_{2} e} $
$tan \alpha = \frac{a_{2}a_{3}}{a_{2}e}$
Now subtitute these values in equation $(1)$, then
$M=\frac{\frac{a_{2}b_{2}}{a_{2} e}}{\frac{a_{2}a_{3}}{a_{2}e}}$
$M=\frac{a_{2}b_{2}}{a_{2}a_{3}}$
Here $a_{2}a_{3} = ab$
So the above equation can be written as
$M=\frac{a_{2}b_{2}}{ab}$
$M=\frac{a_{2}b_{2}}{ab} \frac{a_{1}b_{1}}{a_{1}b_{1}}$
$M=\frac{a_{2}b_{2}}{a_{1}b_{1}} \frac{a_{1}b_{1}}{ab}$
Here $m_{e}=\frac{a_{2}b_{2}}{a_{1}b_{1}}$ and $m_{\circ}= \frac{a_{1}b_{1}}{ab}$
Now substitute the values of $m_{e}$ and $m_{\circ}$ in the above equation
$M=m_{e} \times m_{\circ} \qquad(1)$
Where
$m_{e} \rightarrow$ The linear magnification produced by eye-piece lens system
$m_{\circ} \rightarrow$ The linear magnification produced by the object lens system
So now again from the figure
The linear magnification produced by object lens system $m_{\circ} = -\frac{v_{\circ}}{u_{\circ}}$
The linear magnification produced by eye-piece lens system $m_{e} = \frac{D}{u_{e}}$
Substitute the value of $m_{\circ}$ and $m_{e}$ in equation $(1)$
$M= -\frac{v_{\circ}}{u_{\circ}} \left( \frac{D}{u_{e}} \right) \qquad(2)$
Adjustment of a Compound Microscope:
1.) Adjustment for Clear Vision: In this final image an object is formed at least a distance of distinct vision $D$. For this configuration,
On substitution $u=-u_{e}$, $v=-D$ and $f=f_{e}$ in the lens formula for eyepiece lens
$\frac{1}{-D}+\frac{1}{u_{e}}=\frac{1}{f_{e}}$
$\frac{1}{u_{e}}=\frac{1}{f_{e}} + \frac{1}{D}$
$\frac{D}{u_{e}}= \left( \frac{D}{f_{e}} + 1 \right)$
Now substitute the value of $\frac{D}{u_{e}}$ in equation $(2)$
$M= -\frac{v_{\circ}}{u_{\circ}} \left(1+ \frac{D}{f_{e}} \right) $
The length of the microscope tube in this setup
$L=$ Distance between the object and the eye-piece lenses
$L= v_{\circ} + |u_{e}|$
2.) Adjustment for Relaxed Eye: In this configuration, the final image of an object is formed in a relaxed eye position i.e. at $\infty$. In this setup, the eye-piece lens system is moved back until the image of object $ab$, formed by object lens,i.e., $a_{1}b_{1}$ fall at (coincide with)second focus $f'_{e}$ of the eye-piece lens system. Mathematically this situation comes when $u_{e} = f_{e}$
Thus, the magnifying power in this position,
$M=-\frac{v_{\circ}}{u_{\circ}} \left( \frac{D}{f_{e}} \right)$
For this set the length of the microscope tube,
$L=v_{\circ}+f_{e}$
$m_{e} \rightarrow$ The linear magnification produced by eye-piece lens system
$m_{\circ} \rightarrow$ The linear magnification produced by the object lens system
Difference Between Prism Spectra and Grating Spectra
Prism Spectra
1.) Prism spectra are obtained by the phenomena of dispersion of light.
2.) Prism spectra have only one order.
3.) A prism spectrum is of bright intensity.
4.) In prism spectra, spectral colors overlap each other.
5.) Red color is dispersed least whereas violet color disperses the maximum.
6.) Prism spectrum depends upon the material of prism.
7.) The prism spectral lines are curved.
.
Grating Spectra
1.) Grating spectra are obtained by the phenomena of diffraction of light.
2.) Grating spectra has more than one order.
3.) Grating spectra is of less intensity.
4.) In grating spectra, there is no overlapping of color.
5.) Red color diffracts the maximum whereas violet color diffracts the least.
6.) Grating spectra are independent of the material of grating.
7.) The grating spectral lines are almost straight.
Difference between interference and diffraction
Interference
1.) It is due to the superposition of two or more than two wavefronts coming from coherent sources.
2.) The intensity of all bright fringes are same
3.) Interference fringes either of the same size or decrease after moving away from the center.
4.) Dark fringes are usually perfectly dark.
5.) A minimum coherent source is needed.
Diffraction:
1.) It occurs due to secondary wavelets, originating from infinite different points of the same wavefronts.
2.) Central maxima of bright fringe is followed by either side maxima of decreasing intensity.
3.) Interference fringes are never of the same shape and size.
4.) Dark fringes are not perfectly dark.
5.) It is possible by either one or more than one source which need not be coherent.
Newton's Corpuscular Model
Newton's Corpuscular Theory
In the year 1675, Newton proposed the corpuscular theory of light to explain the existing phenomenon of light. There are the following assumptions of this theory:
1. The light consists of very small, lightweight, and invisible particles. These particles are known as corpuscles.
2. These corpuscles move with the velocity of light in a homogeneous medium in all possible directions in a straight line and they carry kinetic energy with them.
3. When these corpuscles fall on the retina of the eye, they produce the sensation of vision.
4. The size of corpuscles of different colors is different (ie, the color of light depends on the size of the corpuscle).
(A) Success of Carpuscles Theory
Based on this theory, the following facts related to light were explained successfully:
1. The light has energy: Since corpuscles have kinetic energy. Therefore, the energy of the light beam is due to the kinetic energy of the corpuscles.
2. Motion of light along a straight line: Since velocity of the corpuscle is very high, the effect of external forces on it is
negligible. Therefore, it moves in a straight line.
3. Motion of light in vacuum: Corpuscles can move through vacuum.
4. Reflection of light: To explain the reflection of light, Newton assumed that when a corpuscle reaches close to a reflecting surface, then the surface repels it with a force whose direction is perpendicular to the surface and whose magnitude decreases sharply as the distance of corpuscles increases from the surface.
In Figure, let $PO$ be a reflecting surface and $P'Q'$ be an imaginary surface just above it at negligible height. When a light corpuscle moves towards the surface, then it moves along a straight line from $A$ to $B$ (since the force is zero). As it reaches the point $B$ of surface $PQ$, a repulsive force starts acting perpendicular to the surface (upward in the figure). Let $i$ is an angle of incidence at point $B$, then the velocity of the corpuscles at point $B$ has two components- component parallel to surface $V_{||} =v \: sin \: i$ and component perpendicular to surface $V_{|} = v \: cos \: i$. After crossing point $B$, the parallel component remains same but the perpendicular component decreases. At point $C$ of surface $PQ$, the perpendicular component becomes zero. After this direction of the perpendicular component changes and the corpuscles move along path CD. Beyond D again it moves along a straight line as the force becomes ineffective. If $r$ is the angle of reflection at point $D$, then the parallel component of velocity at $D$ will be $v\: sin\: r$. Since the parallel component remains constant. Therefore, comparing them at points $B$ and $D$.
$v \: sin \: i=v \: sin\: r$
$sin \: i= sin\: r$
$i=r$
i.e., the above equation shows that the incident angle and the reflected angle are equal. In the figure above, incident ray, reflected ray and normal all three are in the plane of paper. Therefore laws of reflection are verified.
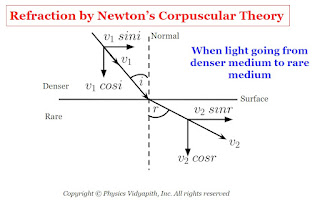
5. Refraction of light: To explain the refraction of light, Newton considered two different situations :
a.) When the light goes from a denser medium to a rare medium: In this condition when the corpuscle reaches near the surface, the surface exerts a normal repulsive force on it. As a result, the perpendicular component of velocity of the corpuscles decreases however it does not reduce to zero as in the case of refraction. Therefore, enters the second medium with a reduced perpendicular component and same constant value of the parallel component i.e., moves along a straight line bending away from normal.
If $i$ and $r$ are the angle of incidence and angle of refraction and $v_{1}$ and $v_{2}$ are the velocity of corpuscle in medium first and second medium. If the parallel component is constant,
$v_{1} \: sin \: i =v_{2} \: sin\: r$
$\frac{sin \: i}{sinr} =\frac{v_{2}}{v_{1}}$
From Figure
$i \lt r$
Therefore
$sin \: i \lt sin\: r$
$v_{2} \lt v_{1}$
Therefore, from the corpuscular theory, velocity light in a denser medium ($v_{1}$) is greater than the velocity light in a rare medium ($v_{2}$).
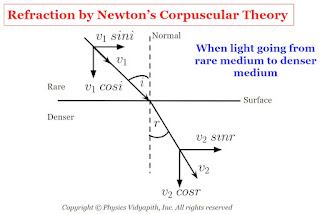
b.) When the light goes from a rare medium to a denser medium: In this condition when the corpuscle reaches near to the surface, the surface attracts it normally. As a result, the normal component of its velocity increases. Therefore, the corpuscular enters the second medium with an increased normal component and the same parallel component of velocity and moves along a straight line bending towards the normal.
$v_{1} \: sin \: i =v_{2} \: sin\: r$
$\frac{sin \: i}{sinr} =\frac{v_{2}}{v_{1}}$
From Figure
$i \gt r$
Therefore
$ sin \: i \gt sin\: r$
$v_{2} \gt v_{1}$
Therefore, velocity light in a denser medium ($v_{1}$) is greater than the velocity light in a rare medium ($v_{2}$).
B) Failure of the Corpuscles Theory
The following are the main reasons for the failure of this theory:
1. Interference, diffraction, polarisation of light, and the photoelectric effect, etc. can not be explained using this principle. For example, in interference, when two light beams interfere, darkness is produced at the same places. It is not possible that two corpuscles destroy each other.
2. According to this theory, the velocity of light is greater in the denser medium as compared to the rare medium. But Focault's had proved experimentally that the velocity of light is less in denser mediums as compared to the velocity of light in rare mediums.
3. According to this theory, greater the temperature of the source greater the velocity of the corpuscles. Actually, the velocity of light does not depend on the temperature of the source.
4. According to this theory, the mass of the source should decrease as it continuously emits corpuscles but it does not happen in reality.
5. In this theory two opposite assumptions are considered to explain reflection and refraction. To explain reflection and refraction through denser to rarer, the repulsive force by the surface is assumed and to explain refraction from rare to denser, the force of attraction by the surface is assumed. These assumptions are opposite and they don't have any scientific base.
Expression for fringe width in Young's double slit experiment
Expression for fringe's width:
Let us consider two wave from slit $S_{1}$ and $S_{2}$ superimpose on each other and form interfernece patteren on the screen. The distance between the two slits is $d$ and distance between slit to screen is $D$. Now take a $n^{th}$ fringe from the centre $O$ of the screen which is at distance $y_{n}$.
So the path difference between the rays
$\Delta x = S_{2}P- S_{1}P \quad(1)$
In $\Delta S_{1}PM$
$S_{1}P^{2}=S_{1}M^{2}+PM^{2} \quad(2)$
From figure:
$S_{1}M =D$
$PM= y_{n}- \left(\frac{d}{2}\right) $
Now subtitute these values in equation $(2)$, then
$S_{1}P^{2}=D^{2}+ \left( y_{n}- \frac{d}{2} \right)^{2} \quad(3)$
In $\Delta S_{2}PN$
$S_{2}P^{2}=S_{2}N^{2}+PN^{2} \quad(4)$
From figure:
$S_{2}N =D$
$PN= y_{n} + \left(\frac{d}{2}\right) $
Now subtitute these values in equation $(4)$, then
$S_{2}P^{2}=D^{2}+ \left( y_{n} + \frac{d}{2} \right)^{2} \quad(5)$
Now subtract the equation $(3)$ in equation $(5)$
$S_{2}P^{2} - S_{1}P^{2} = y_{n} d + y_{n} d $
$ \left( S_{2}P + S_{1}P \right) \left( S_{2}P - S_{1}P \right) = 2y_{n} d$
In this experiment, the distance between slit and screen i.e. $D$ is much greater than the distance between the slit i.e. $d$ so angle $\theta$ will be very small. So from figure
$S_{1}P = S_{2}P = D$
Substitute this value in the equation $(6)$, therefore equation $(6)$ can be written as
$ 2D \Delta x = 2y_{n} d $
$D \Delta x = y_{n}$
$\Delta x = \frac{y_{n} d}{D} \quad (7) $
This is equation of path differnce between two wave from slit $S_{1}$ and slit $S_{2}$.
Condition For Bright Fringe:
The path difference for bright fringe is
$\Delta x= n \lambda \qquad(8)$
From equation $(7)$ and equation $(8)$
$n \lambda = \frac{ d}{D} $
$y_{n} = \frac{n \lambda D}{d} \quad(9)$
This is the equation for distance of $n^{th}$ bright fringe. Now the distance of $(n+1)^{th}$ bright fringe.
$y_{n+1} = \frac{\left( n+1 \right) \lambda D}{d} \quad(10)$
The dark fringe lie between the two consecutive bright fringe. So width of the dark fringe
$\beta = y_{n+1} - y_{n}$
Now subtitute the value of $y_{n+1}$ and $y_{n}$ in the above equation $(9)$ and equation $(10)$, then
$\beta = \frac{\left( n+1 \right) \lambda D}{d} - \frac{n \lambda D}{d}$
$\beta = \frac{\lambda D}{d} \quad(11)$
This is the equation of width of dark fringe.
Condition For Dark Fringe:
The path difference for dark fringe is
$\Delta x = (2n-1) \lambda \quad(12)$
From equation $(7)$ and equation $(12)$
$ (2n-1) \lambda = \frac{y_{n} d}{D} $
$y_{n} = \frac{(2n-1) \lambda D}{d} \quad(13)$
This is the equation for distance of $n^{th}$ dark fringe. Now the distance of $(n+1)^{th}$ dark fringe.
$y_{n+1} = \frac{\left[ 2 (n+1)-1) \right] \lambda D}{d} $
$y_{n+1} = \frac{(2n+1)\lambda D}{d} \quad(14)$
The bright fringe lie between the two consecutive dark fringe. So width of the bright fringe
$\beta = y_{n+1} - y_{n}$
Now subtitute the value of $y_{n+1}$ and $y_{n}$ in the above equation $(13)$ and equation $(14)$, then
$\beta = \frac{(2n+1)\lambda D}{d} - \frac{(2n-1) \lambda D}{d}$
$\beta = \frac{\lambda D}{d} \quad(15)$
This is the equation of width of bright fringe.
The equation $(11)$ and equation $(15)$ shows that the width of bright fring and dark fringe is same.
Alternative method to find the path differnce of two wave in Young's double-slit Experiment
Let us consider: Two wave from slit $S_{1}$ and $S_{2}$ superimpose on each other and form interfernece patteren on the screen.
The distance between the two slits is $\rightarrow d$
The distance between slit to screen is $\rightarrow D$
The distance of $n^{th}$ fringe from the centre $O$ of the screen is $\rightarrow y_{n}$.
So the path difference between the two rays is
$\Delta x = S_{2}M \quad(1)$
Now from figure, In $\Delta S_{1}S_{2}M$
$sin \theta = \frac{S_{2}M}{S_{1}S_{2}} \quad(2)$
In $\Delta PNO$
$tan \theta = \frac{PO}{NO} \quad(3)$
The distance between slit and screen i.e. $D$ is much greater than the distance between the slit i.e. $d$ so angle $\theta$ will be very small i.e. $sin \theta \approx tan \theta \approx \theta $. Now equate the equation $(2)$ and equation $(3)$
$\frac{PO}{NO} = \frac{S_{2}M}{S_{1}S_{2}} \quad(4)$
Now the value from the above figure
$\frac{y_{n}}{D} = \frac{\Delta x}{d} $
$\Delta x = \frac{y_{n} d}{D} $
This is the equation of the path difference between two wave from slit $S_{1}$ and $S_{2}$.
Now the derivation for the condition for Bright and Dark fringe can be used here as it is given above.
$PM= y_{n}- \left(\frac{d}{2}\right) $
$PN= y_{n} + \left(\frac{d}{2}\right) $
$S_{2}P^{2} - S_{1}P^{2} = \left[D^{2}+ \left( y_{n} + \frac{d}{2} \right)^{2}\right] - \left[ D^{2}+ \left( y_{n}- \frac{d}{2} \right)^{2} \right] $
$S_{2}P^{2} - S_{1}P^{2} = D^{2}+ \left( y_{n} + \frac{d}{2} \right)^{2} - D^{2} - \left( y_{n}- \frac{d}{2} \right)^{2} $
$S_{2}P^{2} - S_{1}P^{2} = \left( y_{n} + \frac{d}{2} \right)^{2} - \left( y_{n}- \frac{d}{2} \right)^{2} $
$S_{2}P^{2} - S_{1}P^{2} = y^{2}_{n} + \left(\frac{d}{2}\right)^{2} +2 y_{n} \left(\frac{d}{2}\right) - y^{2}_{n} - \left(\frac{d}{2}\right)^{2} +2 y_{n} \left(\frac{d}{2}\right) $
$S_{2}P^{2} - S_{1}P^{2} = y^{2}_{n} + \left(\frac{d}{2}\right)^{2} + y_{n} d - y^{2}_{n} - \left(\frac{d}{2}\right)^{2} + y_{n} d $
$ \left( S_{2}P + S_{1}P \right) \Delta x = 2y_{n} d \quad \left\{from \: equation\: (1)\right\} \qquad(6)$
Analytical expression of intensity for constructive and destructive interference due to Young's double slit
Analytical expression of intensity for interference due to Young's double slit:
Let us consider two waves from slit $S_{1}$ and $S_{2}$ having amplitude $a_{1}$ and $a_{2}$ respectively superimpose on each other at point $P$ . If the displacement of waves is $y_{1}$ and $y_{2}$ and the phase difference is $\phi$ then
$y_{1}=a_{1} \: sin \omega t \qquad(1)$
$y_{2}=a_{2} \: sin \left( \omega t + \phi \right) \qquad(2)$
According to the principle of superposition:
$y=y_{1}+y_{2} \qquad(3)$
Now substitute the value of $y_{1}$ and $y_{2}$ in the above equation $(3)$
$y=a_{1} \: sin \omega t + a_{2} \: sin \left( \omega t + \phi \right)$
Let
$a_{1} + a_{2} \: cos \phi = A\: cos\theta \qquad(5)$
$a_{2} \: sin \phi = A\: sin\theta \qquad(6)$
Now the above equation $(4)$ can be written as
$y= A\: cos\theta \: sin \omega t + A\: sin\theta \: cos \omega t $
$y= A \left( cos\theta \: sin \omega t + sin\theta \: cos \omega t \right)$
$y= A \: sin \left( \omega t + \theta \right) \qquad(7)$
This is the equation of the resultant displacement of the waves from slit $S_{1}$ and $S_{2}$ at point $P$ on the screen.
Now square the equation $(5)$ and equation $(6)$ and then add to them so
$ A^{2} = a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} \: cos\phi \qquad(8)$
$ A = \sqrt{ a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} \: cos\phi }\qquad(9)$
Resultant Intensity:
The resultant intensity at point $P$ due waves from slit $S_{1}$ and $S_{2}$ can be find by flollowing formula:
$I=A^{2}$
Now subtitute the va;ue of $A^{2}$ from equation $(8)$ in the above equation
$I= a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} \: cos\phi \qquad(10)$
$I= I_{1} + I_{2} + 2\sqrt{I_{1} \: I_{2}} \: cos\phi \qquad(11)$
Constructive Interference:
For constructive interference the $cos\phi$ should be equal to +1 i.e. $cos\phi =1$
Phase Difference in Constructive Interference:
We know that for constructive interference $cos\phi =1$
$cos\phi = cos( 2n\pi)$
$\phi = 2n\pi \qquad(12)$
Path difference in Constructive Interference:
We know that the path difference
$\Delta x = \frac{\lambda}{2 \pi} \phi$
Now subtitute the value of $\phi $ from equation $(12)$ in the above equation
$\Delta x = \frac{\lambda}{2 \pi} 2n\pi$
$\Delta x = n \lambda \qquad(13)$
Resultant Amplitude due to Constructive Interference:
For constructive interference, the resultant amplitude is maximum at point $P$. So from equation $(9)$
$ A_{max} = \sqrt{ \left (a_{1} + a_{2} \right)^{2}} $
$ A_{max} = \left( a_{1} + a_{2} \right) \qquad(14)$
For constructive interference, the resultant amplitude of the waves is the sum of the amplitude of individual waves.
Resultant Intensity due to Constructive Interference:
For constructive interference, the resultant intensity is maximum at point $P$. So from equation $(10)$
$I_{max}=\left( a_{1} + a_{2} \right)^{2} \qquad(15)$
From equation $(11)$
$I_{max}= I_{1} + I_{2} + 2\sqrt{I_{1} \: I_{2}} \qquad(16)$
Destructive Interference:
For destructive interference the $cos\phi$ should be equal to -1 i.e. $cos\phi = -1$
Phase Difference in Destructive Interference:
We know that for destructive interference $cos\phi = -1$
$cos\phi = cos \left( \left( 2n \pm 1 \right)\pi \right)$
$\phi = \left( 2n \pm 1 \right)\pi \qquad(17)$
Path difference in Destructive Interference:
We know that the path difference
$\Delta x = \frac{\lambda}{2 \pi} \phi$
Now subtitute the value of $\phi $ from equation $(17)$ in the above equation
$\Delta x = \frac{\lambda}{2 \pi} \left( 2n \pm 1 \right)\pi$
$\Delta x = \left( 2n \pm 1 \right) \frac{\lambda}{2} \qquad(18)$
Resultant Amplitude due to Destructive Interference:
For the destructive interference, the resultant amplitude is minimum at point $P$. So from equation $(9)$
$ A_{min} = \sqrt{ \left (a_{1} - a_{2} \right)^{2}} $
$ A_{min} = \left( a_{1} - a_{2} \right)$
For constructive interference, the resultant amplitude of the waves is the difference in amplitude of individual waves.
Resultant Intensity due to Destructive Interference:
For the destructive interference, the resultant intensity is minimum at point $P$. So from equation $(10)$
$I_{min}=\left( a_{1} - a_{2} \right)^{2}$
From equation $(11)$
$I_{min}= I_{1} + I_{2} - 2\sqrt{I_{1} \: I_{2}} $
$y=a_{1} \: sin \omega t + a_{2} \left( sin \omega t \: cos \phi + cos \omega t \: sin \phi \right) $
$y=a_{1} \: sin \omega t + a_{2} \: sin \omega t \: cos \phi + a_{2}\: cos \omega t \: sin \phi $
$y= \left( a_{1} + a_{2} \: cos \phi \right) \: sin \omega t + a_{2} \: sin \phi \: cos \omega t \qquad(4)$
$ A^{2} \: sin^{2}\theta + A^{2}\: cos^{2}\theta = \left( a_{1} + a_{2} \: cos \phi \right)^{2} + a^{2}_{2} \: sin^{2} \phi $
$ A^{2} \left( sin^{2}\theta + cos^{2}\theta \right) = a^{2}_{1} + a^{2}_{2} \: cos^{2} \phi + 2a_{1} \: a_{2} \: cos\phi + a^{2}_{2} \: sin^{2} \phi $
$ A^{2} = a^{2}_{1} + a^{2}_{2} \left( cos^{2}\phi + sin^{2}\phi \right) + 2a_{1} \: a_{2} \: cos\phi $
$ A_{max} = \sqrt{ a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} } \qquad \left( \because cos\phi =+1 \right)$
$I_{max}= a^{2}_{1} + a^{2}_{2} + 2a_{1} \: a_{2} \qquad \left( \because cos\phi =+1 \right)$
$ A_{min} = \sqrt{ a^{2}_{1} + a^{2}_{2} - 2a_{1} \: a_{2} } \qquad \left( \because cos\phi =-1 \right)$
$I_{min}= a^{2}_{1} + a^{2}_{2} - 2a_{1} \: a_{2} \qquad \left( \because cos\phi =-1 \right)$
Combined Focal Length and Power of two thin lenses in contact
Derivation of the combined focal length and power of two thin lenses in contact:
Case (1): When both are convex lens-
a.) The combined focal length of two thin convex lenses in contact:
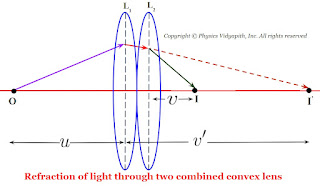
Let us consider that two convex lenses $L_{1}$ and $L_{2}$ are connected with transparent cement Canada Balsam. If the focal length of the lenses is $f_{1}$ and $f_{1}$ and an object $O$ is placed at distance $u$ from the first lens $L_{1}$ and its image $I'$ is formed at a distance $v'$ from the first lens $L_{1}$. Therefore from the equation of focal length for lens $L_{1}$
$\frac{1}{f_{1}} = \frac{1}{v'} - \frac{1}{u} \qquad(1)$
For the second lens, The image $I'$ works as a virtual object for the second lens $L_{2}$ which image $I$ is formed at a distance $v$ from the second lens $L_{2}$. Therefore from the equation of focal length for lens $L_{2}$
$\frac{1}{f_{2}} = \frac{1}{v} - \frac{1}{v'} \qquad(2)$
Now add the equation $(1)$ and equation $(2)$. then
$\frac{1}{f_{1}} + \frac{1}{f_{2}} = \frac{1}{v'} - \frac{1}{u} + \frac{1}{v} - \frac{1}{v'} $
$\frac{1}{f_{1}} + \frac{1}{f_{2}} = \frac{1}{v} - \frac{1}{u} $
Where $ \frac{1}{f} = \frac{1}{v} - \frac{1}{u} $
$\frac{1}{f_{1}} + \frac{1}{f_{2}} = \frac{1}{f} \qquad(3)$
$\frac{1}{f} = \frac{f_{1} + f_{2}}{f_{1}f_{2}} $
$f = \frac{f_{1}f_{2}}{f_{1} + f_{2}} $
This is the equation of the combined focal length of two thin convex lenses in contact.
b.)The combined power of two thin convex lenses in contact:
We know that the power of the lens equation
$P = \frac{1}{f}$
So from equation $(3)$
$P=P_{1} + P_{2}$
This is the equation of the combined power of two thin convex lenses in contact.
Similarly for another two cases $(2)$ and case $(3)$:
Case (2): When both are concave lens-
a.) The combined focal length of two thin concave lenses in contact:
For concave lenses the focal length for both lenses i.e. ($f_{1} \: and \: f_{2}$) will be negative. Therefore the combined focal length of the two thin concave lens
$ \frac{1}{f} = \frac{1}{- f_{1}} + \frac{1}{- f_{2}} $
$\frac{1}{f} =- \frac{\left(f_{1} + f_{2} \right)}{f_{1}f_{2}} $
$f = -\frac{f_{1}f_{2}}{f_{1} + f_{2}} $
b.) The combined power of two thin concave lenses in contact:
$P= - \left(P_{1} + P_{2}\right)$
Case (3): When one lens is convex and the second is concave-
a.) The combined focal length of two thin lenses for convex and concave:
If the focal length of convex lens is $f_{1}$ and for concave is $f_{2}$ then the combine focal length of lenses
$ \frac{1}{f} = \frac{1}{ f_{1}} + \frac{1}{- f_{2}} $
$\frac{1}{f} = \frac{\left(f_{1} - f_{2} \right)}{f_{1}f_{2}} $
$f = \frac{f_{1}f_{2}}{f_{1} - f_{2}} $
b.) The combined power of two thin lenses for convex and concave:
$P= \left(P_{1} - P_{2}\right)$
Refraction of light through a thin lens : Lens maker's formula
Derivation of refraction of light through a thin lens & Lens maker's formula:
Let us consider, A convex lens having thickness $t$ and radius of curvature of surfaces is $R_{1}$ and $R_{2}$. If an object $O$ is placed at distance $u$ from the first surface of the convex lens and its image $I'$ is formed at distance $v'$ from the first surface of the convex lens then refraction of light through the first spherical surface of the lens
$ \frac{\left( n_{2} - n_{1} \right)}{R_{1}} = \frac{n_{2}}{v'} - \frac{n_{1}}{u} \qquad(1) $
Now the Image $I'$ works as a virtual object for the second surface of the convex lens which image $I$ formed at distance $v$ from the second surface of the lens. So refraction of light through the second surface of the lens
$ \frac{\left( n_{1} - n_{2} \right)}{R_{2}} = \frac{n_{1}}{v} - \frac{n_{2}}{v' - t} $
Here $t$ is the thickness of the lens. If the lens is very thin then thickness will be $t=0$. Therefore above equation for second surface of the lens can be written as
$ \frac{\left( n_{1} - n_{2} \right)}{R_{2}} = \frac{n_{1}}{v} - \frac{n_{2}}{v'} \qquad(2) $
Now add the equation $(1)$ and equation $(2)$, So
$\frac{\left( n_{2} - n_{1} \right)}{R_{1}} + \frac{\left( n_{1} - n_{2} \right)}{R_{2}} = \frac{n_{2}}{v'} - \frac{n_{1}}{u} + \frac{n_{1}}{v} - \frac{n_{2}}{v'} $
$\frac{\left( n_{2} - n_{1} \right)}{R_{1}} + \frac{\left( n_{1} - n_{2} \right)}{R_{2}} = - \frac{n_{1}}{u} + \frac{n_{1}}{v} $
$\left( n_{2} - n_{1} \right) \left( \frac{1}{R_{1}} - \frac{1}{R_{2}} \right) =n_{1} \left( \frac{1}{v} - \frac{1}{u} \right) $
$n_{1} \left( \frac{1}{v} - \frac{1}{u} \right) = \left( n_{2} - n_{1} \right) \left( \frac{1}{R_{1}} - \frac{1}{R_{2}} \right) $
$ \left( \frac{1}{v} - \frac{1}{u} \right) = \frac{\left( n_{2} - n_{1} \right)}{n_{1}} \left( \frac{1}{R_{1}} - \frac{1}{R_{2}} \right) $
We know that the equation of the focal length of a lens
$\frac{1}{f} = \frac{1}{v} - \frac{1}{u}$
Where $f \rightarrow$ Focal length of convex lens. Now substitute the value of $f$ in the above equation
$ \frac{1}{f} = \frac{\left( n_{2} - n_{1} \right)}{n_{1}} \left( \frac{1}{R_{1}} - \frac{1}{R_{2}} \right)$
$ \frac{1}{f} = \left( \frac{n_{2}}{n_{1}} - 1 \right) \left( \frac{1}{R_{1}} - \frac{1}{R_{2}} \right)$
$ \frac{1}{f} = \left( n - 1 \right) \left( \frac{1}{R_{1}} - \frac{1}{R_{2}} \right) \qquad \left( \because \frac{n_{2}}{n_{1}}= n\right)$
The above equation represents the equation of refraction of light through a thin lens and lens maker's formula.
Refraction of light through the convex spherical surface
Derivation of refraction of light through the convex spherical surface:
Let us consider, a convex spherical surface which has radius of curvature $R$. If an object $O$ is placed at a distance $u$ from pole $P$ and its image $I$ is formed at distance $v$ from pole $P$ and the angle subtended by the object, image, and center of curvature is $\alpha$, $\beta$, and $\gamma$ then from figure
In $\Delta MOC$
$i= \gamma + \alpha \qquad(1)$
In $\Delta MIC$
$r = \gamma + \beta \qquad(2)$
According to Snell's Law:
$\frac{sin \: i}{sin \: r} = \frac{n_{2}}{n_{1}} \qquad(3)$
Here the aperture of the spherical surface is very small so point $M$ will be very close to point $P$ and angle $i$ and $r$ will be small. So
$sin \: i \approx i$
$sin \: r \approx r$
So equation $(3)$ can be written as
$\frac{ i}{ r} = \frac{n_{2}}{n_{1}} \qquad(4)$
Now subtitute the value of $i$ and $r$ from equation $(1)$ and equation $(2)$ in equation $(4)$
$\frac{ \left( \gamma + \alpha \right)}{\left( \gamma + \beta \right)} = \frac{n_{2}}{n_{1}} $
$ \left( \gamma + \alpha \right) n_{1} = \left( \gamma + \beta \right) n_{2} $
$ \gamma \: n_{1} + \alpha \: n_{1} = \gamma \: n_{2} + \beta \: n_{2} $
$ \gamma \: n_{1} - \gamma \: n_{2} = \beta \: n_{2} - \alpha \: n_{1} $
$ \left( n_{1} - n_{2} \right) \gamma = \beta \: n_{2} - \alpha \: n_{1} \qquad(5)$
Again here the aperture of the spherical surface is very small so point $N$ will be very close to point $P$. Therefore the angle $\alpha$, $\beta$, and $\gamma$ will be very small. Then in $\Delta MON$
$\alpha = tan \alpha = \frac {MN}{ON} \approx \frac{MN}{OP} = \frac{h}{-u}$
Similarly for angle $\beta$ and $\gamma$, Apply in $\Delta MIN$ and $\Delta MCN$
$\beta = tan \beta = \frac {MN}{IN} \approx \frac{MN}{IP} = \frac{h}{-v}$
$\gamma = tan \gamma = \frac {MN}{CN} \approx \frac{MN}{CP} = \frac{h}{R}$
Now subtitute the value of $\alpha$, $\beta$, and $\gamma$ from above in equation $(5)$
$ \left( \frac{h}{R} \right) \left( n_{1} - n_{2} \right) = \left( \frac{h}{-v} \right) n_{2} - \left( \frac{h}{-u} \right) n_{1} $
$ \frac{\left( n_{2} - n_{1} \right)}{R} = \frac{n_{2}}{v} - \frac{n_{1}}{u} $
This is the equation of refraction of light through a convex spherical surface.
Another form of the above equation:
$ n_{1} \frac{\left( \frac{n_{2}}{n_{1}} - 1 \right)}{R} = n_{1} \frac{\frac{n_{2}}{n_{1}}}{v} - \frac{1}{u} $
$ n_{1} \frac{\left( \frac{n_{2}}{n_{1}} - 1 \right)}{R} = n_{1} \frac{\left(\frac{n_{2}}{n_{1}}\right)}{v} - \frac{1}{u} $
$ \frac{\left( \frac{n_{2}}{n_{1}} - 1 \right)}{R} = \frac{\left(\frac{n_{2}}{n_{1}}\right)}{v} - \frac{1}{u} $
$ \frac{\left( n - 1 \right)}{R} = \frac{n}{v} - \frac{1}{u} \qquad \left( \because \frac{n_{2}}{n_{1}}= n\right) $
Where $n \rightarrow Refractive \: index \: of \: glass \: with \: respect \: to \: air$
This is another form of the equation of refraction of light through a convex spherical surface.
$sin \: r \approx r$
Refraction of light through the concave spherical surface
Derivation of refraction of light through the concave spherical surface:
Let us consider, a concave spherical surface of radius of curvature $R$. If an object $O$ is placed at a distance $u$ from pole $P$ and its image $I$ is formed at distance $v$ from pole $P$ and the angle subtended by the object, image, and center of curvature is $\alpha$, $\beta$, and $\gamma$ then from figure
In $\Delta MOC$
$\gamma= \alpha + i $
$i= \gamma - \alpha \qquad(1)$
In $\Delta MIC$
$\gamma= \beta + r $
$r = \gamma - \beta \qquad(2)$
According to Snell's Law:
$\frac{sin \: i}{sin \: r} = \frac{n_{2}}{n_{1}} \qquad(3)$
Here the aperture of the spherical surface is very small so point $M$ will be very close to point $P$ and angle $i$ and $r$ will be small. So
$sin \: i \approx i$
$sin \: r \approx r$
So equation $(3)$ can be written as
$\frac{ i}{ r} = \frac{n_{2}}{n_{1}} \qquad(4)$
Now subtitute the value of $i$ and $r$ from equation $(1)$ and equation $(2)$ in equation $(4)$
$\frac{ \left( \gamma - \alpha \right)}{\left( \gamma - \beta \right)} = \frac{n_{2}}{n_{1}} $
$ \left( \gamma - \alpha \right) n_{1} = \left( \gamma - \beta \right) n_{2} $
$ \gamma \: n_{1} - \alpha \: n_{1} = \gamma \: n_{2} - \beta \: n_{2} $
$ \gamma \: n_{1} - \gamma \: n_{2} = -\beta \: n_{2} + \alpha \: n_{1} $
$ \left( n_{1} - n_{2} \right) \gamma = -\beta \: n_{2} + \alpha \: n_{1} \qquad(5)$
Again here the aperture of the spherical surface is very small so point $N$ will be very close to point $P$. Therefore the angle $\alpha$, $\beta$, and $\gamma$ will be very small. Then in $\Delta MON$
$\alpha = tan \alpha = \frac {MN}{ON} \approx \frac{MN}{OP} = \frac{h}{-u}$
Similarly for angle $\beta$ and $\gamma$, Apply in $\Delta MIN$ and $\Delta MCN$
$\beta = tan \beta = \frac {MN}{IN} \approx \frac{MN}{IP} = \frac{h}{-v}$
$\gamma = tan \gamma = \frac {MN}{CN} \approx \frac{MN}{CP} = \frac{h}{-R}$
Now subtitute the value of $\alpha$, $\beta$, and $\gamma$ from above in equation $(5)$
$ \left( \frac{h}{-R} \right) \left( n_{1} - n_{2} \right) = - \left( \frac{h}{-v} \right) n_{2} + \left( \frac{h}{-u} \right) n_{1} $
$ \frac{\left( n_{2} - n_{1} \right)}{R} = \frac{n_{2}}{v} - \frac{n_{1}}{u} $
This is the equation of refraction of light through a concave spherical surface.
Another form of the above equation:
$ n_{1} \frac{\left( \frac{n_{2}}{n_{1}} - 1 \right)}{R} = n_{1} \frac{\frac{n_{2}}{n_{1}}}{v} - \frac{1}{u} $
$ n_{1} \frac{\left( \frac{n_{2}}{n_{1}} - 1 \right)}{R} = n_{1} \frac{\left(\frac{n_{2}}{n_{1}}\right)}{v} - \frac{1}{u} $
$ \frac{\left( \frac{n_{2}}{n_{1}} - 1 \right)}{R} = \frac{\left(\frac{n_{2}}{n_{1}}\right)}{v} - \frac{1}{u} $
$ \frac{\left( n - 1 \right)}{R} = \frac{n}{v} - \frac{1}{u} \qquad \left( \because \frac{n_{2}}{n_{1}}= n\right) $
Where $n \rightarrow Refractive \: index \: of \: glass \: with \\ respect \: to \: air$
This is another form of the equation of refraction of light through a concave spherical surface.
$sin \: r \approx r$
Refraction of light and its Properties
Definition of Refraction of light→
When a light goes from one medium to another medium then light bends from the path. This bending of the light phenomenon is knowns as the refraction of light.
When light goes from a rarer medium to a denser medium, light bends toward the normal as shown in the figure below:
When light goes from a denser medium to a rarer medium, the light goes away from normal as shown in the figure below.
Properties of refraction of light→
$\frac{sin \: i}{sin \: r}=constant(_{1}n_{2}) $
$\frac{sin \: i}{sin \: r}= (_{1}n_{2})$
$\frac{sin \: i}{sin \:r}=\frac{n_{2}}{n_{1}}$
Where $_{1}n_{2}$ is the refractive index of medium $(2)$ with respect to medium $(1)$ .
Absolute refractive index→
The ratio of the speed of light in a vacuum to the speed of light in a medium is called the absolute refractive index of the medium.
$refractive\: index(n)=\frac{speed\: of\:light\: in\: vacuum(c)}{speed \:of \:light\: in\: medium(v)}$
$n=\frac{c}{v}$
Note
According to Snell's law -
$\frac{sin \: i}{sin \: r}=\frac{n_{2}}{n_{1}} \quad\quad (1)$
$\frac{sin \: i}{sin \: r}=\frac{\frac{c}{v_{1}}}{\frac{c}{v_{2}}} \quad\quad \left \{ \because n=\frac{c}{v} \right \}$
$\frac{sin i}{sin r}=\frac{v_{1}}{v_{2}} \qquad (2)$
When the light goes from one medium to another medium frequency of the light does not change but the wavelength of the light changes. So above given equation can be written as
$\frac{sin \: i}{sin \: r}=\frac{\nu \lambda_{1}}{\nu \lambda_{2}} \quad\quad \left \{ \because v=\nu \lambda \right \} $
$\displaystyle \frac{sin \: i}{sin \: r}=\frac{\lambda_{1}}{ \lambda_{2}} \qquad (3)$
From equation $(1)$ ,equation $(2)$, and equation $(3)$ we can write the equation
$\frac{sin \: i}{sin \: r}=\frac{n_{2}}{n_{1}} =\frac{v_{1}}{v_{2}}= \frac{\lambda_{1}}{ \lambda_{2}}$
Conditions for a light ray to pass undeviated on refraction of light→
A ray of light passes undeviated from medium $1$ to medium $2$ in either of the following two conditions:
Factors affecting the refractive index of the medium→
The refractive index of a medium depends on basically following three factors:
1. Nature of the medium (on the basis of speed of light)→
Less the speed of light in the medium as compared to that in the air more is the refractive index of the medium.
$\left ( n=\frac{c}{v}\right)$
Speed of light in glass- $v_{glass} = 2\times 10^{6} ms^{-1}$
$\mu_{glass} = 1\cdot 5$
Speed of light in water- $v_{water} = 2\cdot25\times10^8ms^{-1}$
$\mu_{water} = 1\cdot33$
2. Physical conditions such as temperature→
With the increase in temperature, the speed of light in the medium, so the refractive index of the medium decreases.
3. The colour or wavelength of light→
The speed of light of all colours is the same in the air ( or vacuum), but in any other transparent medium, the speed of light is different for different colours. In a given medium the speed of red light is maximum and that of the violet light is least, therefore the refractive index of that medium is maximum for violet is and least for red light i.e. $\left ( \ n_{violet}> n_{red}\right )$. The wavelength of visible light increase from violet to red end, so the refractive index of a medium decreases with the increases in wavelength.
 |
| Propagation of light from rarer medium to denser medium |
 |
| Propagation of light from denser medium to rarer medium |
- The incident ray, normal ray, and refracted ray lie on the same point.
- According to Snell's law - The ratio of the sine of the incident angle to the sine of the refractive angle is always constant. This constant value is known as the refractive index of the medium.
- When the angle of incidence at the boundary of two media is zero $\angle i =0^{\circ} so \ \angle r= 0^{\circ}$.
- When the refractive index of the medium (2) and medium (1) is the same i.e. $i=r$.
Difference between Fraunhofer and Fresnel diffraction
Difference between Fraunhofer Diffraction and Fresnel Diffraction→
| S.No. | Fresnel Diffraction | Fraunhofer Diffraction |
|---|---|---|
| 1. | The distance between source to slit and slit to screen is finite. | The distance between source to slit and slit to screen is infinite. |
| 2. | The shape of the incident wavefront on the slit is spherical or cylindrical. | The shape of the incident wavefront on the slit is plane. |
| 3. | The shape of the incident wavefront on the screen is spherical or cylindrical. | The shape of the incident wavefront on the screen is a plane. |
| 4. | There is a path difference created between the rays before entering the slit. This path difference depends on the distance between the source and slit. | There is not any path difference between the rays before entering the slit. |
| 5. | Path difference between the rays forming the diffraction pattern depends on the distance of the slit from the source as well as the screen and the angle of diffraction. Hence the mathematical treatment is complicated. | Path difference depends only on the angle of diffraction. Hence the mathematical treatment is comparatively easier. |
| 6. | Lenses are not required to observe or perform Fresnel diffraction in the laboratory. | Lenses are required to observe or perform Fraunhofer diffraction in the laboratory. |
Missing Order in double slit diffraction pattern
The equation for missing order in the double-slit diffraction pattern→
The nature of the diffraction pattern due to the double slits depends upon the relative values of $e$ and $d$. If, however, $e$ is kept constant and $d$ is varied, then certain orders of interference maxima will be missing.
We know that, the direction of interference maxima
$(e+d)\:sin\theta=\pm n\lambda \qquad(1)$
The direction of diffraction minima
$e \: sin\theta=\pm m\lambda \qquad(2)$
Divide the equation $(1)$ by equation $(2)$
$\frac{(e+d)}{e}=\frac{n}{m}$
Case (I)→
If $e=d$ then
n=2m
So for $m=1,2,3,....$
The $n=2,4,6,....$
Thus, the $2_{nd}, 4^{th}, 6^{th}, ...$ order interference maxima will be missing.
Case (II) →
If $e=\frac{d}{2}$ then
n=3m
So for $m=1,2,3,....$
The $n=3,6,9,....$
Thus, the $3_{rd}, 6^{th}, 9^{th}, ...$ order interference maxima will be missing.
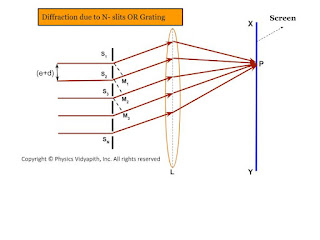
Diffraction due to a plane diffraction grating or N- Parallel slits
A diffraction grating (or $N$-slits) consists of a large number of parallel slits of equal width and separated from each other by equal opaque spaces.
It may be constructed by ruling a large number of parallel and equidistance lines on a plane glass plate with the help of a diamond point. the duplicates of the original grating are prepared by pouring a thin layer of colloidal solution over it and then allowed to Harden. This layer is then removed from the original grating and fixed between two glass plates which serve as a plane transmission grating. Generally, A plane transmission grating has 10000 to 15000 lines per inch.
Theory→
Since plane diffraction grating is an $N$-slit arrangement, the deflection pattern due to it will be the combined diffraction effect of all such slits. Let a plane wavefront of monochromatic light be incident normally on the $N$-parallel slit of the gratings. Each point within the slits then sends out secondary wavelets in all directions.
Let $e$ be the width of each slipped and $d$ be the separation between any two consecutive slits then $(e+d)$ is known as the grating element. The diffracted ray from each slit, then $(e+d)$ is knowns as the grating element. The diffracted ray from each slit is focussed at a point $P$ on the screen $XY$ with the help of a convex lens $L$.
Expression for Intensity→
Let $S_{1}, S_{2}, S_{3},.......$ be the middle point of each slit and $S_{1}M_{1}, S_{2}M_{2}, S_{3}M_{3}, ........S_{N-1}M_{N-1}$ be the perpendicular drawn as shown in the figure.The waves diffracted from each slit are equivalent to a single wave amplitude:
$R=\frac{A\:sin\alpha}{\alpha} \qquad(1)$
The path difference between the waves from slit $S_{1}$ and $S_{2}$ is
$S_{2}M_{1}=(e+d)sin\theta$
The path difference between the waves from slit $S_{2}$ and $S_{3}$ is
$S_{3}M_{2}=(e+d)sin\theta$
The path difference between the waves from slit $S_{n-1}$ and $S_{n}$ is
$S_{N}M_{N-1}=(e+d)sin\theta$
Thus, it is obvious that the path difference between all the consecutive waves is the same and equal to $(e+d)sin\theta$
The corresponding phase difference
$\Delta \phi=\frac{2\pi}{\lambda}(e+d)sin\theta \qquad(2)$
Let $\Delta \phi=2\beta$
$\beta=\frac{\pi}{\lambda}(e+d)sin\theta \qquad(3)$
Thus, the resultant amplitude at $P$ is the resultant amplitude of $N$ waves, each of amplitude $R$ and its common phase difference is $(2\beta)$
$R'=\frac{R \: sin \left( \frac{2N\beta}{2} \right) }{sin \left( \frac{2\beta}{2} \right)} \qquad(4)$
The resultant amplitude at $P$
$R'=\frac{R \: sin N\beta}{sin \beta} $
Where $R=\frac{A\: sin\alpha}{\alpha}$. Now substitute the value of $R$ in the above equation and we get
$R'= \frac{A\: sin\alpha}{\alpha} \frac{ \: sin N\beta}{sin \beta} \qquad(5)$
The resultant intensity at $P$
$I=R'^{2}$
$I=\frac{A^{2} \: sin^{2} \alpha}{\alpha^{2}} \frac{ \: sin^{2} N\beta}{sin^{2} \beta} \qquad(6)$
The factor $\frac{A^{2} \: sin^{2} \alpha}{\alpha^{2}}$ gives the intensity pattern due to diffraction from a single slit while the factor $\frac{ \: sin^{2} N\beta}{sin^{2} \beta}$ gives the distribution of intensity due to interference from all the $N$-slit
Principle Maxima→
The intensity will be maximum when $sin\beta=0$ or $\beta=\pm n\pi$
Where $n=0,1,2,3,.....$
But under this condition, $sinN\beta$ is also equal to zero. Hence term $\frac{sin N\beta}{sin \beta}$ can be solve by
$\lim_{\beta \rightarrow \pm n\pi} \frac{ \: sin N\beta}{sin \beta}=\lim_{\beta \rightarrow \pm n\pi} \frac{\frac{d}{d\beta} (sin N\beta)}{\frac{d}{d\beta}(sin \beta)}$
$\lim_{\beta \rightarrow \pm n\pi} \frac{ \: sin N\beta}{sin \beta}=\lim_{\beta \rightarrow \pm n\pi} \frac{N cos N\beta}{cos \beta}$
$\lim_{\beta \rightarrow \pm n\pi} \frac{ \: sin N\beta}{sin \beta}=N \lim_{\beta \rightarrow \pm n\pi} \frac{ cos N\beta}{cos \beta}$
Where the value of $\lim_{\beta \rightarrow \pm n\pi} \frac{ cos N\beta}{cos \beta}=1$
$\lim_{\beta \rightarrow \pm n\pi} \frac{ \: sin N\beta}{sin \beta}=N \qquad(7)$
So the maximum intensity
$I=\frac{A^{2} \: sin^{2} \alpha}{\alpha^{2}} N^{2} \qquad(8)$
Thus, the condition for principle maxima
$sin \beta=0$
$\beta=\pm n\pi$
$(e+d)sin\theta=\pm n \lambda \qquad(9)$
For $n=0$, we get $\theta=0$ This $\theta=0$ gives the direction of zero-order principal maxima. For the value of $n=1,2,3,......$, gives the direction of first, second, third,....... order principal maxima.
Minima →
The intensity will be minimum, when $sin N\beta=0$ but $sin\beta=0$
$N\beta=\pm m\pi$
$N(e+d)sin\theta=\pm m \lambda \qquad(10)$
Where $m$ can take all integral values except $0, N,2N,3N,......$ because for these values of $m$, $sin\beta=0$ which gives the position of principal maxima.
Secondary maxima→
It is obvious from the above condition of minima, there are $(N-1)$ minima between two successive principal maxima. Hence, there are $(N-2)$ other maxima with alternative minima between two successive principal maxima. These $(N-2)$ maxima are called secondary maxima. To find the condition of secondary maxima equation $(6)$ is differentiated with respect to $\beta$ and equated to zero.
$\frac{dI}{d\beta}= \frac{A^{2}\:sin^{2}\alpha}{\alpha^{2}}2 \frac{sinN\beta}{sin\beta} \left [\frac{sin\beta . N. cosN\beta-sinN\beta . cos\beta}{sin^{2}\beta} \right ]$
$0= \frac{A^{2}\:sin^{2}\alpha}{\alpha^{2}}2 \frac{sinN\beta}{sin\beta} \left [\frac{sin\beta . N. cosN\beta-sinN\beta . cos\beta}{sin^{2}\beta} \right ]$
$N.sin\beta . cosN\beta - sinN \beta . cos\beta=0$
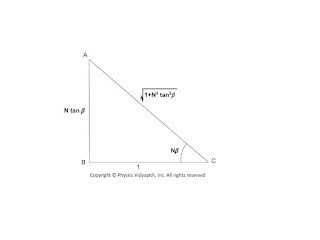
$\tan N\beta = N tan \beta \qquad(11)$
Now construct a right-angled triangle with the sides according to the above equation$(11)$
From the above triangle:
$sinN\beta=\frac{N tan\beta}{\sqrt{1+N^{2}tan^{2}\beta}} \qquad(12)$
Substituting the value of $sinN\beta$ from the above equation to equation (6)
$I=\frac{A^{2} \: sin^{2} \alpha}{\alpha^{2}} \frac{N^{2} tan^{2}\beta}{1+N^{2}tan^{2}\beta} \frac{ 1}{sin^{2} \beta}$
$I=\frac{A^{2} \: sin^{2} \alpha}{\alpha^{2}} \frac{N^{2}}{1+N^{2}tan^{2}\beta} \frac{ 1}{cos^{2} \beta} \qquad \left(\because tan\beta =\frac{sin\beta}{cos\beta} \right)$
$I=\frac{A^{2} \: sin^{2} \alpha}{\alpha^{2}} \frac{N^{2}}{cos^{2} \beta+N^{2}sin^{2}\beta} $
$I=\frac{A^{2} \: sin^{2} \alpha}{\alpha^{2}} \frac{N^{2}}{1- sin^{2} \beta+N^{2}sin^{2}\beta} $
$I=\frac{A^{2} \: sin^{2} \alpha}{\alpha^{2}} \frac{N^{2}}{1+(N^{2}-1) sin^{2} \beta} \qquad(12)$
Now divide the equation $(12)$ by equation $(8)$ so
$\frac{Intensity\: of\:secondary\:maxima}{Intensity\:of\:principal\:maxima}=\frac{1}{1+(N^{2}-1) sin^{2} \beta}$
It is obvious from the above equation that When $N$ increases then the intensity of secondary maxima decreases.
 |
| Diffraction due to N- slits OR Grating |
 |
| Right-angled Triangle for Intensity Calculation |
 |
| Intensity distribution diagram due to a diffraction grating |
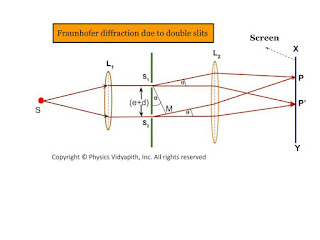
Fraunhofer diffraction due to a double slit
Let a plane wavefront be incident normally on slit $S_{1}$ and $S_{2}$ of equal $e$ and separated by an opaque distance $d$.The diffracted light is focused on the screen $XY$. The diffracted pattern on the screen consists of equally spaced bright and dark fringe due to interference of light from both the slits and modulated by diffraction pattern from individual slits.
op
The diffraction pattern due to double-slit can be explained considering the following points →
All the points in slits $S_{1}$ and $S_{2}$ will send secondary waves in all directions.
All the secondary waves moving along the incident wave will be focussed at $P$ and the diffracted waves will be focussed at $P'$
The amplitude at $P'$ is the resultant from two slit each of amplitude $R=\frac{A\:sin\alpha}{\alpha}$
T two waves from two-slit $S_{1}$ and $S_{2}$ will interfere at $P'$
Expression for Intensity →
$\Delta = S_{2}M$
$\Delta=(e+d)sin\theta\qquad(1)$
The corresponding phase difference →
$\Delta\phi= \frac{2\pi}{\lambda}(e+d)sin\theta \qquad(2)$
Let $\Delta \phi =2 \beta \qquad(3)$
$\beta=\frac{\pi}{\lambda}(e+d)sin\theta\qquad(4)$
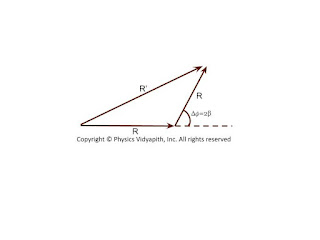
The resultant amplitude at $P'$ can be obtained by the vector addition method. The resultant amplitude at $P'$
$R'^{2}=R^{2}+R^{2}+2R.R.cos\Delta\phi$
$R'^{2}=R^{2}+R^{2}+2R.R.cos2\beta$ {\qquad $\because 2\beta=\Delta\phi$}
$R'^{2}=2R^{2}+2R^{2}cos2\beta$
$R'^{2}=2R^{2} \left( 1+cos2\beta \right)$
$R'^{2}=4R^{2} cos^{2}\beta \qquad(5)$
Where $R$ - Resultant amplitude of each slit $S_{1}$
$R=\frac{A\: sin\alpha}{\alpha} \qquad(6)$
Substituting the value of $R$ in equation $(5)$
$R'^{2}=4 A^{2} \frac{sin^{2}\alpha}{\alpha^{2}} cos^{2} \beta \qquad(7)$
$R'=2 A \frac{sin\alpha}{\alpha} cos\beta \qquad(8)$
The intensity of the resultant diffraction pattern at $P'$
$I=4 A^{2} \frac{sin^{2}\alpha}{\alpha^{2}} cos^{2} \beta \qquad(9)$
Where $\alpha=\frac{\pi}{\lambda}e\:sin\theta \qquad(10)$
The resultant intensity at any point is the contribution of the following two factors →
The factor $\frac{A^{2}sin^{2}\alpha}{\alpha^{2}}$, represents the intensity distribution due to diffraction from any individual slits.
The factor $cos^{2}\beta$ represents the intensity distribution due to interference of waves from two parallel slits.
Condition for Maxima and Minima →
1. Maxima and minima due to diffraction term →
i.) Principal Maxima →
The diffraction term $\frac{A^{2}sin^{2}\alpha}{\alpha^{2}}$ gives the central maxima, for $\alpha=0$ so
$\frac{\pi}{\lambda}e\: sin\theta=0$
$sin\theta =0 $
$\theta=0$
ii.) Minima →
The diffraction term $\frac{A^{2}sin^{2}\alpha}{\alpha^{2}}$ gives the central minima, for $sin\alpha=0$ so
$\alpha=\pm m\pi$
$e\:sin\theta=\pm m\pi$
iii.) Secondary Maxima →
The secondary maxima are obtained in the direction given by →
$\alpha= \pm\frac{3\pi}{2},\pm\frac{5\pi}{2},\pm\frac{7\pi}{2},..............$
2. Maxima and minima due to interference term →
i.) Maxima→
The interference term $cos^{2}\beta$ gives maxima in the direction →
$cos^{2}=1$
$\beta=\pm n \pi$
$\frac{\pi}{\lambda}(e+d)sin\theta= \pm n \pi$
$(e+d)sin\theta= \pm n \lambda$
Where $n=0,1,2,3,.....$
In the direction $\theta=0^{\circ}$, the principle maxima due to interference and diffraction coincide.
ii.) Minima→
The interference term $cos^{2}\beta$ gives minima in the direction →
$cos^{2}\beta=0$
$\beta=\pm(2n+1)\frac{\pi}{2}$
$(e+d)sin\theta=\pm(2n+1)\frac{\pi}{2}$
The intensity distribution curve due to the diffraction term, interference term, and the combined effect is shown in the figure below →
 |
| Fraunhofer diffraction due to double slits |
 |
| Resultant Vector |
- Maxima and minima due to diffraction term
- Maxima and minima due to interference term
 |
| Intensity diagram of Fraunhofer double slit Experiment |
Popular Posts
-
Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is ...
-
Angle of Acceptance → "If incident angle of light on the core for which the incident angle on the core-cladding interface equals t...
-
Derivation of interference of light due to a wedge-shaped thin film: Interference of light due to wedge-shaped thin film The wedge...
-
Maxwell's Equations: Maxwell's equation of the electromagnetic wave is a collection of four equations i.e. Gauss's law of elec...
-
Let a plane wavefront be incident normally on slit $S_{1}$ and $S_{2}$ of equal $e$ and separated by an opaque distance $d$.The diffracted l...
Study-Material
Categories
Alternating Current Circuits
(10)
Atomic and Molecular Physics
(4)
Biomedical
(1)
Capacitors
(6)
Classical Mechanics
(12)
Current carrying loop in magnetic field
(5)
Current Electricity
(10)
Dielectric Materials
(1)
Electromagnetic Induction
(3)
Electromagnetic Wave Theory
(23)
Electrostatic
(22)
Energy Science and Engineering
(2)
Error and Measurement
(2)
Gravitation
(11)
Heat and Thermodynamics
(3)
Kinematics Theory Of Gases
(2)
Laser System & Application
(15)
Magnetic Effect of Current
(9)
Magnetic Substances
(3)
Mechanical Properties of Fluids
(5)
Nanoscience & Nanotechnology
(4)
Nuclear Physics
(7)
Numerical Problems and Solutions
(2)
Optical Fibre
(5)
Optics
(25)
Photoelectric Effect
(3)
Quantum Mechanics
(37)
Relativity
(8)
Semiconductors
(2)
Superconductors
(1)
Topic wise MCQ
(9)
Units and Dimensions
(1)
Waves
(5)