Mutual Induction Phenomenon and its Coefficient

  November 17, 2023   
Mutual Induction:

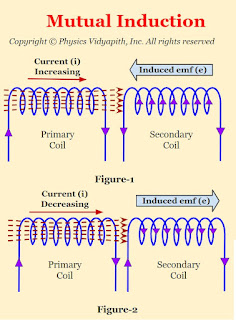
When two coils are placed near each other then the change in current in one coil ( Primary Coil) produces electro-motive force $\left( emf \right)$ in the adjacent coil ( i.e. secondary coil). This phenomenon is called the principle of Mutual Induction.

The direction of electro-motive force $\left( emf \right)$ depends or can be found by "Lenz's Law"

Mathematical Analysis of Coefficient of Mutual Induction:

Let us consider that two coils having the number of turns are $N_{1}$ and $N_{2}$. If these coils are placed near to each other and the change in current of the primary coil is $i_{1}$, then linkage flux in the secondary coil will be
Mutual Induction between two coils
$N_{2}\phi_{2} \propto i_{1}$

$N_{2}\phi_{2} = M i_{1} \qquad(1)$

Where $M$ $\rightarrow$ Coefficient of Mutual Induction.

According to Faraday's law of electromagnetic induction. The electro-motive force $\left( emf \right)$ in the secondary coil is

$e_{2}=-N_{2}\left( \frac{d \phi_{2}}{dt} \right)$

$e_{2}=-\frac{d \left(N_{2} \phi_{2} \right)}{dt} \qquad(2)$

From equation $(1)$ and equation $(2)$

$e_{2}=-\frac{d \left(M i_{1} \right)}{dt} $

$e_{2}=-M \left(\frac{d i_{1}}{dt} \right) $

$M = \frac{e_{2}}{\left(\frac{d i_{1}}{dt} \right)}$

If $\left(\frac{d i_{1}}{dt} \right) = 1$

Then

$M = e_{2}$

The above equation shows that If the rate of flow of current in the primary coil is unit then the coefficient of mutual induction will be equal to the induced electro-motive force $\left( emf \right)$ in the secondary coil.