Derivation of variation of mass with velocity:
Consider two systems of reference (frame of reference) $S$ and $S’$. The frame $S’$ is moving with constant velocity $v$ relative to frame $S$.
Let two bodies of masses $m_{1}$ and $m_{2}$ be traveling with velocities $u’$ and $-u’$ parallel to the x-axis in the system $S’$. Suppose the two bodies collide and after collision coalesce into one body.
The principles of conservation of mass and of momentum also hold good in relativity same as in classical mechanics. So now apply the principle of conservation of momentum.
Apply the law of addition of velocities, the velocities $u_{1}$ and $u_{1}$ in the system $S$ corresponding to $u’$ and $-u’$ in frame $S’$ are given by $\rightarrow$
$u_{1}= \frac{u'+v}{1+\frac{u'v}{c^{2}}}\quad or \quad u_{2}= \frac{-u'+v}{1-\frac{u'v}{c^{2}}}\qquad(2)$
Now substitute the value of $u_{1}$ and $u_{1}$ in equation $(1)$
A point or a particle at any instant, in space has different cartesian coordinates in the different reference systems. The equation which provide the relationship between the cartesian coordinates of two reference system are called Transformation equations.
Galilean Transformation Equation:
Let us consider, two frames $S$ and $S'$ in which frame $S'$ is moving with constant velocity $v$ relative to an inertial frame $S$. Let
The origin of the two frames coincide at $t=0$
The coordinate axes of frame $S'$ are parallel to that of the frame $S$ as shown in the figure below
The velocity of the frame $S'$ relative to the frame $S$ is $v$ along x-axis;
The position vector of a particle at any instant $t$ is related by the equation
The equation $(1)$ and equation $(2)$ express the transformation of coordinates from one inertial frame to another. Hence they are referred to as Galilean transformation.
The equation $(1)$ and equation $(2)$ depending on the relative motion of two frames of reference, but it also depends upon certain assumptions regarding the nature of time and space. It is assumed that the time t is independent of any particular frame of reference. i.e. If $t$ and $t'$ be the times recorded by observers $O$ and $O'$ of an event occurring at $P$ then
$ t=t'\qquad (3)$
Now add the above assumption with transformation equation $(3)$ so the Galilean transformation equations are
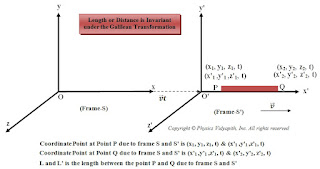
The other assumption, regarding the nature of space, is that the distance between two points (or two particles) is independent of any particular frame of reference. For example if a rod has length $L$ in the frame $S$ with the end coordinates $(x_{1}, y_{1}, z_{1})$ and $(x_{2}, y_{2}, z_{2})$ then
So from equation $(5)$, equation $(6)$ and equation $(7)$, we can write as:
$L=L'$
Thus, the length or distance between two points is invariant under Galilean Transformation.
The hypothesis of Galilean Invariance:(Principle of Relativity)
The hypothesis of Galilean invariance is based on experimental observation and is stated as follows:
The basic laws of physics are identical in all reference system which move with uniform velocity with respect to one another.
OR in other words
The basics laws of physics are invariant in inertial frame.
Modify the hypothesis of Galilean Invariance by giving the following statement-
The basic law of physics are invariant in form in two reference system which are connected by Galilean Transformation
Failure of Galilean Relativity OR Galilean Transformation:
There are the following points that could not explain by Galilean transformation:
Galilean Transformation failed to explain the actual result of the Michelson-Morley experiment.
It violates the postulates of the Special theory of relativity.
According to Maxwell's electromagnetic theory, the speed of light in a vacuum is $c$ $(3\times10^{8} m/sec)$ in all directions. Let us consider a frame of reference relative to which the speed of light is $c$ in all directions, According to Galilean transformation the speed of light in any other inertial system, which is in relative motion with respect to the former, will be different in a different direction. For example- If an observer is moving with speed $v$ opposite or along with the propagation of light, The speed of light $c_{0}$ in the frame of the observer is given by
Length Contraction (Lorentz-Fitzgerald Contraction):
Lorentz- Fitzgerald, first time, proposed that When a body moves comparable to the velocity of light relative to a stationary observer, then the
length of the body decreases along the direction of velocity. This decrease in length in the direction of motion is called 'Length Contraction'.
Expression for Length Contraction:
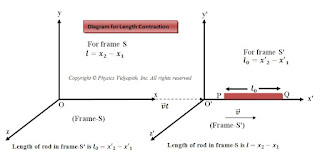
Let us consider two frames $S$ and $S'$ in which frame $S'$ is moving with constant velocity $v$ relative to frame $S$ along the positive x-axis direction. Let a rod is associated with frame $S'$. The rod is at rest in frame $S'$ so the actual length $l_{0}$ is measured by frame $S'$. So
$ l_{0}=x'_{2}-x'_{1}\quad\quad (1)$
Where $x'_{2}$ and $x'_{1}$ are the x-coordinate of the ends of the rod in frame $S'$.
According to Lorentz's Transformation
$ x'_{1}=\alpha (x_{1}-vt)\quad\quad (2)$
$ x'_{2}=\alpha (x_{2}-vt)\quad\quad (3)$
Now put the value of $x'_{1}$ and $x'_{2}$ in equation $(1)$, then
Here $l$ is the length of the rod measured in frame $S$.
Here The factor $\sqrt{1-\frac{v^{2}}{c^{2}}}$ is less than unity. It means
that
$ \sqrt{1-\frac{v^{2}}{c^{2}}}< 1 $
so
$l< l_{0}$
So the length of the rod in frame $S$ will be less than the proper length or
actual length which is measured in frame $S'$.
Case:
If $v=c$, Then $l=0$, i.e. a rod moving with the velocity of light will
appear as a point to a stationary observer. So from the above discussion, we
can conclude that in relativity there is no absolute length'.
**What is the proper length?
The length of the rod is measured by a stationary observer relative to the length of the rod in the frame.
Time Dilation (Apparent Retardation of Clocks):
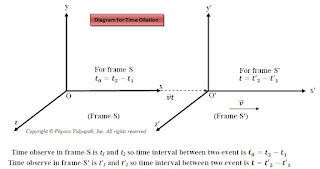
Let us consider two frames $S$ and $S'$ in which frame $S'$ is moving with constant velocity $v$ relative to frame $S$ along the positive x-axis direction.
Let two events occur in frame $S$ which is at rest at time $t_{1}$ and $t_{2}$. These two event measured in frame $S'$ at time $t'_{1}$ and
$t'_{2}$. So time interval between these two events in frame $S'$ is
Here the factor $\sqrt{1-\frac{v^{2}}{c^{2}}}$ is less then unity. i.e
$ \sqrt{1-\frac{v^{2}}{c^{2}}}< 1$
Then
$t> t_{0}$
So the time interval between two events in frame $S'$ will be longer than the time interval taken in frame $S$.
The time dilation is a real effect. All clocks will appear running slow for
an observer in relative motion. It is incorrect to say that the clock in
moving frame $S'$ is slow as compared to the clock in stationary frame $S$. The
correct statement would be that All clocks will run slow for an observer in
relative motion.
Case:
If $v=c$, then $t=∞ $ i.e. When a clock moving with the speed of light appears to be completely stopped to an observer in a stationary frame of reference.
** Proper and Non-Proper Time:
The time interval between two events that occur at the same position recorded by a clock in the frame in which the events occur (or frame at rest) is called 'proper time'.
The time interval between the same two events recorded by an observer in a frame that is moving with respect to the clock is known as 'Non -proper time or relativistic time'.
Experimental Verification of Time Dilation:
The direct experimental confirmation of time dilation is found in an experiment on cosmic ray particles called mesons. μ-mesons are created at
high altitudes in the earth's atmosphere (at the height of about 10 km) by the interaction of fast cosmic-ray photons and are projected towards the earth's surface with a very high speed of about $2.994\times10^{8}$ m/s which is $0.998$ of the speed of light $c$. μ-mesons are unstable and decay into electrons or positrons with an average lifetime of about $2.0\times10^{-6}$sec. Therefore, in its lifetime a μ-mesons can travel a
distance.
Now the question arises how μ-mesons travel a distance of 10 km to reach the earth's surface. This is possible because of the time dilation effect. In fact, μ-mesons have an average lifetime $t_{0}=2.0\times10^{-6}$ sec in their own frame of reference. In the observer's frame of reference on the earth's surface, the lifetime of the μ-mesons is lengthened due to relativity effects to the value $t$ given as,
Let us consider two inertial frames $S$ and $S'$ in which frame $S'$ is moving with constant velocity $v$ along the positive x-axis direction
relative to the frame $S$. Let $t$ and $t'$ be the time recorded in two frames. Let the origin $O$ and $O'$ of the two reference systems coincide at $t=t'=0$.
Now suppose, a source of light is situated at the origin $O$ in the frame $S$, from which a wavefront of light is emitted at time $t=0$. When
the light reaches point $P$, the time required by a light signal in travelling the distance OP in the Frame $S$ is
$ t=\frac{OP}{c}$
$ t=\frac{\left (x^{2}+y^{2}+z^{2} \right )}{c}$
$ x^{2}+y^{2}+z^{2}=c^{2}t^{2}\qquad (1)$
The equation $(1)$ represents the equation of wavefront in frame $S$. According to the special theory of relativity, the velocity of light will be $c$ in the second frame $S'$. Hence in frame $S'$ the time required by the light signal in travelling the distance $O'P$ is given by
$ t'=\frac{O'P}{c}$
$ x'^{2}+y'^{2}+z'^{2}=c^{2}t^{2}\qquad (2)$
According to the Galilean transformation equation:
Now substitute these values in equation $(2)$ then we get
$ (x-vt)^{2}+y^{2}+z^{2}=c^{2}t^{2}$
$ x^{2}+v^{2}t^{2}-2xvt+y^{2}+z^{2}-c^{2}t^{2}=0$
The above equation is certainly not same as the equation $(1)$ because it contains an extra term $(-2xvt+v^{2}t^{2})$. Thus the Galilean transformation fails.
Further $t=t'$ because $\left( t=\frac{OP}{c} \: and \: t'=\frac{O'P}{c} \right)$ which does not agree with Galilean transformation equations.
The extra term $(-2xvt+v^{2}t^{2})$ indicates that transformations in $x$ and $t$ should be modified so that this extra term is cancelled. So modification in transformation
$ x'=\alpha (x-vt) \quad for \: x'=0,\: x=vt$
$ t'=\alpha (t+fx)$
Where $α$, $α'$ and $f$ are constant to be determined for Galilean Transformations $α= α'=1$ and $f=0$. Now substituting these modified values in equation $(2)$ so
These equations are called Lorentz Transformations because they were first obtained by Dutch Physicist H. Lorentz.
The above transformation equation shows that frame $S'$ is moving in positive x-direction with velocity $v$ relative to the frame $S$. But if we
say that frame $S$ is moving with $v$ velocity relative to frame $S'$ along negative x-direction then the transformation is:
Let us consider two frames $S$ and $S'$, frame $S'$ is moving with constant velocity $v$ relative to frame $S$ along the positive direction of the X-axis.
Let us express the velocity of the body in these frames. Suppose that body moves a distance $dx$ in time $dt$ in frame $S$ and through a distance $dx'$ in the time $dt'$ in the system $S'$ from point $P$ to $Q$. Then
From equation $(1)$. The above equation can be written as:
$u = \frac{u' +v}{1+ \frac{u'v}{c^{2}}} $
This equation represents the relativistic law of addition of velocities with respect to an observer at frame-$S$ whereas in classical mechanics it is simply $u = u'+v$. There is the following point observed from the addition of the velocities equation.
When $u'$ and $v$ are the smaller as compare to $c$, then $\frac{v\cdot u'}{c^{2}}$ can be negligible so
$u = u'+v$
which is classical formula.
When $u' = c$Then $u =\frac{c+v}{1+\frac{v}{c}}$ So,
$u=c$
Therefore a object moves with velocity of light $c$ with respect to other, then their relative velocity is always $c$.
When $v=u'=c$Then $u =\frac{c+c}{1+\frac{c^{2}}{c^{2}}}=c$ So,
$u=v$
This shows that the addition of the velocity of light simply reproduces the velocity of light. It means that the velocity of light in a vacuum is the maximum achievable velocity in nature and no signal and any object can travel faster than the velocity of light in a vacuum.
Now substitute the value of $dk$ from equation $(5)$ in equation $(7)$. So above equation can be written as:
$dk = c^{2}dm$
Now consider that the particle is at rest initially and by the application of force it acquires a velocity $v$. The mass of body increase from ${m_{\circ}}$ to $m$. The total kinetic energy acquired by the particle is given by
$dk = \int_{m_\circ}^{m}c^{2}\cdot dm$
$k = c^{2}\left ( m-m_{\circ} \right )$
$k = mc^{2} - m_\circ c^{2}$
$k+m_\circ c^{2} = mc^{2}$
Where $k$ is the kinetic energy of the particle and $m_\circ c^{2}$ is the rest mass-energy of the particle. So The sum of these energies is equal to the total energy of the particle $E$. So
Concept of Simultaneity (Relative character of Time ):
The interval aren't the same for two observes in relative motion. This cause an important incontrovertible fact that two events that appear to happen simultaneously to at least one observer are not simultaneous to another observer in relative motion.
Suppose two events occur (or two-time bombs explode) at different places $x_{1}$ and $x_{2}$ but at the same time $t_{0}$ with respect to an observer in a stationary frame (or on the ground). The situation of the different to an observer in moving frame $S'$ or to a pilot of a spaceship moving with velocity $v$ relative to stationary frame $S$ (or ground). To him, according to Lorentz transformation for time.
The explosion at $x_{1}$ occurs at
Hence the two events (explosions) that occur simultaneously to one observer in the stationary frame are separated to another observer in a moving frame by an interval of
Therefore, the principle of simultaneity in relativity is an absolute concept for two events. It depends on an observer or a frame of reference. The effect is not due to the time dilation. Hence, we conclude that there is no such thing as “absolute time” which is the same for all observers.
“Time is relative and it varies for all observers in relative motion.”
It is assumed that space is continuous and the motion of particles in space can be described by their position at different instants of time. The position of a particle is known as a point in space. These points are described by the coordinate system in space.
When point (position of particle in space) and the time are taken together then it is called an Event.
The coordinate system of a particle which describe the position of any particle relative to it, then such coordinate system is known as Frame of Reference or System of Reference.
Absolute Space:
The absolute space is those frame of reference relative to which every motion and position should be measured.
Types of Frame of Reference:
According to the motion of particles frame of reference is divided into two categories
Inertial frame of reference
Non-inertial frame of reference
Inertial frame of reference:
Those unaccelerated frame of reference, in which Newton's first and second laws hold, are called inertial frames.
In an inertial frame, body does not experience any force so according to second law of Newton-
$F=ma \qquad (1)$
$F=0$
so from equation $(1)$
$ ma=0$
$ a=0$
$ \frac{d^2r}{dt^2}=0\qquad (2)$
In component form, above equation, can be written as:
Discussion of Inertial Frame in terms of relative frame of reference:
Let us consider an inertial frame $S$ and another frame $S'$ which is moving with constant velocity $v$ relative to frame $S$. If the position of the origins of the two frames coincide, then in the two frames the position vector of any particle $P$ at any instant $t$ can be related by the following expression-
Now we conclude that "If a frame is an inertial frame then all those frames which are moving with constant velocity relative to the first frame are also inertial"
Non-inertial Frame:
Those frames of reference in which Newton's law of inertia does not hold are called non-inertial frames.
All the accelerated and rotating frames are the non-inertial frames of reference.
According to Newton's Second Law, the force $F$ applied on a body of mass $m$ is given by
$ F_{i}=ma_{i}\qquad (1)$
Newton's Second Law is not valid when a body of mass $m$ self accelerated and accelerated body will observe the acceleration $a_{N}$. Hence
$ F_{i}\neq ma_{N}\qquad (2)$
If no external force is acting on a particle. Even then in the accelerated frame, It will appear that a force is acting on it. This force is called pseudo force or fictitious force. The direction of force is opposite to acceleration.
$ F_{o}\neq ma_{o}\qquad (3)$
Discussion of Non-inertial Frame in term of relative frame of reference:
Let us consider, an inertial frame $S$ and another frame $S'$ is moving with an acceleration $a_{0}$ relative to frame $S$.
The principles of conservation of mass and of momentum also hold good in relativity same as in classical mechanics. So now apply the principle of conservation of momentum.
