Definition of Gravitational Potential:
When an object is brought from infinity to a point in the gravitational field then work done acquired by the gravitational force is called gravitational potential.
Let us consider, An object of mass $m$ brought from infinity to a point in the gravitational field. If work done acquired by force is $W$ then gravitational potential
$V=-\frac{W}{m}$
Derivation of Gravitational Potential due to a Point mass:
Let us consider,
The mass of the point object (i.e point mass)=$m$
The mass of the object that produces the gravitational field = $M$
If the point mass $m$ is at a distance $x$ then the gravitational force between the objects is
$F=G \frac{M \: m}{x^{2}} \qquad(1)$
If the point mass moves a very small distance element $dx$ that is at distance $x$ from point $O$ then the work done to move the point object from point $B$ to $A$
$dw=F.dx$
Now substitute the value of $F$ from equation $(1)$ in above equation
$dw=G \frac{M \: m}{x^{2}}.dx$
Therefore, the work done to bring the point mass from infinity to point $P$ that is at distance $r$ from point $O$ then work done to move the point object from infinity ($\infty$) to point $P$
$\int_{0}^{W} dw = \int_{\infty}^{r} G \frac{M \: m}{x^{2}}.dx $
$ [w]_{0}^{W} = G\: M\: m \int_{\infty}^{r} \frac{1}{x^{2}}.dx $
$ [W-0] = G\: M\: m [-\frac{1}{x} ]_{\infty}^{r} $
$ W = G\: M\: m [\left(-\frac{1}{r}\right) - \left(-\frac{1}{\infty}\right)]$
$ W = -\frac{G\: M\: m }{r} \qquad \left( \because \frac{1}{\infty} =0 \right)$
$ W = -\frac{G\: M\: m }{r} $
$\frac{W}{m} = -\frac{G\: M }{r} $
$ V = -\frac{G\: M}{r} \qquad \left( \because V=\frac{W}{m} \right)$
$ V = -\frac{G\: M}{r}$
Thus the above equation represents the gravitational potential at point $P$
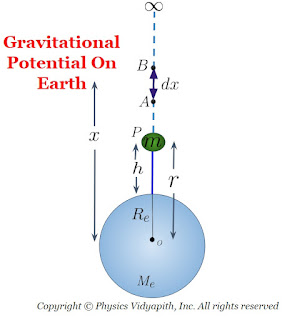
Gravitational Potential on Earth:
Let us consider,
The mass of Earth = $M_{e}$
The radius of earth = $R_{e}$
The mass of the object = $m$
The distance from centre $O$ of the earth to point $P$ = $r$
The distance from the surface of the earth to point $P$ = $h$
If the object is at a distance $x$ then the gravitational force is
$F=G \frac{M_{e} \: m}{x^{2}} \qquad(1)$
If the object moves a very small distance element $dx$ that is at distance $x$ from centre point $O$ of the earth then the work done to move an object from point $B$ to $A$
$dw=F.dx$
Now substitute the value of $F$ from equation $(1)$ in above equation
$dw=G \frac{M_{e} \: m}{x^{2}}.dx$
Therefore, the work done to bring the object from infinity to point $P$ that is at distance $r$ from centre point $O$ of the earth then the work done to move an object from infinity ($\infty$) to point $P$
$\int_{0}^{W} dw = \int_{\infty}^{r} G \frac{M_{e} \: m}{x^{2}}.dx $
$ [w]_{0}^{W} = G\: M_{e}\: m \int_{\infty}^{r} \frac{1}{x^{2}}.dx $
$ [W-0] = G\: M_{e}\: m [-\frac{1}{x} ]_{\infty}^{r} $
$ W = G\: M_{e}\: m [\left(-\frac{1}{r}\right) - \left(-\frac{1}{\infty}\right)]$
$ W = -\frac{G\: M_{e}\: m }{r} \qquad \left( \because \frac{1}{\infty} =0 \right)$
$ W = -\frac{G\: M_{e}\: m }{r} $
$\frac{W}{m} = -\frac{G\: M_{e} }{r} $
$ V = -\frac{G\: M_{e}}{r} \qquad \left( \because V=\frac{W}{m} \right)$
$ V = -\frac{G\: M_{e}}{r}$
Where $r=R_{e}+h$, then above equation can be written as
$V=-\frac{G \: M_{e}}{R_{e}+h} \qquad(2)$
This is the equation of gravitational potential at point $P$. The other form of the above equation i.e
$V=-\frac{g R_{e}^{2}}{R_{e}+h} \qquad \left( \because GM_{e}= g R_{e}^{2} \right)$
If the object is placed on the surface of the earth then $h=0$. So gravitational potential on the surface of the earth
$V=-\frac{G \: M_{e}}{R_{e}}$
This is the equation of gravitational potential on the surface of the earth. The other form of the above equation is
$V=-\frac{g R_{e}^{2}}{R_{e}} \qquad \left( \because GM_{e}= g R_{e}^{2} \right)$
$V=-g R_{e}$