Four Level Pumping in Laser

Description:

In four-level pumping, atoms of ground energy state go to upper energy state$(E_{4})$ by pumping transition to achieve the population inversion. Due to the short time of the upper energy state atoms go to metastable state by nonradiative transitions or spontaneous emission. Atoms of metastable state come to lower lasing level by laser transition process. The atoms come from lower lasing level to ground state by nonradiative transition or spontaneous emission. This process is repeated continuously.

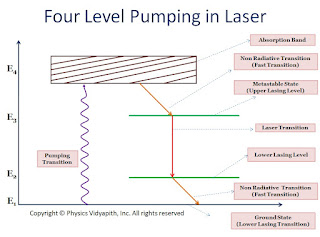Four-level pumping in Laser

In contrast to level pumping, the lower lasing transition level in the four-level scheme is not the ground state and is virtually vacant. As soon as some atoms are pumped to the upper lasing level, population inversion is achieved. So it is required less pumping energy than a three-level laser system. this is the major disadvantage of this scheme. Further, the lifetime of the lower lasing level is shorter as it is not a metastable state. Hence atom in level $E_{2}$ quickly drops to the ground state. This depletion of the $E_{2}$ energy level helps sustain the population inversion by avoiding and accumulation of atoms in the lower lasing level. Therefore four-level laser system can operate in a continuous wave mode.

Comments

Numerical Aperture and Acceptance Angle of the Optical Fibre

Angle of Acceptance → If incident angle of light on the core for which the incident angle on the core-cladding interface equals the critical angle then incident angle of light on the core is called the "Angle of Acceptance. Transmission of light when the incident angle is equal to the acceptance angle If the incident angle is greater than the acceptance angle i.e. $\theta_{i}>\theta_{0}$ then the angle of incidence on the core-cladding interface will be less than the critical angle due to which part of the incident light is transmitted into cladding as shown in the figure below Transmission of light when the incident angle is greater than the acceptance angle If the incident angle is less than the acceptance angle i.e. $\theta_{i}<\theta_{0}$ then the angle of incidence on the core-cladding interface will be greater than the critical angle for which total internal reflection takes place inside the core. As shown in the figure below Transmission of lig

click here »

Fraunhofer diffraction due to a single slit

Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is incident normally from $S$ on a narrow slit $AB$ of width $e$ and is diffracted from it. The diffracted beam is focused at the screen $XY$ by another converging lens $L_{2}$. The diffraction pattern having a central bright band followed by an alternative dark and bright band of decreasing intensity on both sides is obtained. Analytical Explanation: The light from the source $S$ is incident as a plane wavefront on the slit $AB$. According to Huygens's wave theory, every point in $AB$ sends out secondary waves in all directions. The undeviated ray from $AB$ is focused at $C$ on the screen by the lens $L_{2}$ while the rays diffracted through an angle $\theta$ are focussed at point $p$ on the screen. The rays from the ends $A$ and $B$ reach $C$ in the same phase and hence the intensity is maximum. Fraunhofer diffraction due to

click here »

Particle in one dimensional box (Infinite Potential Well)

Let us consider a particle of mass $m$ that is confined to one-dimensional region $0 \leq x \leq L$ or the particle is restricted to move along the $x$-axis between $x=0$ and $x=L$. Let the particle can move freely in either direction, between $x=0$ and $x=L$. The endpoints of the region behave as ideally reflecting barriers so that the particle can not leave the region. A potential energy function $V(x)$ for this situation is shown in the figure below. Particle in One-Dimensional Box(Infinite Potential Well) The potential energy inside the one -dimensional box can be represented as $\begin{Bmatrix} V(x)=0 &for \: 0\leq x \leq L \\ V(x)=\infty & for \: 0> x > L \\ \end{Bmatrix}$ $\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2m}{\hbar^{2}}(E-V)\psi(x)=0 \qquad(1)$ If the particle is free in a one-dimensional box, Schrodinger's wave equation can be written as: $\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2mE}{\hbar^{2}}\psi(x)=0$ $\frac{d^{2} \psi(x)}{d x

click here »

Physics Vidyapith ✍️

Search This Blog