Nanoparticles and Its Properties
Introduction:
The prefix 'nano' means a billionth ($10^{-9}$). The field of nanotechnology is the study of various structures of matter having dimensions of the order of a billionth of a meter. These particles are called nanoparticles. Nanotechnology is based on the fact that particles that are smaller than about $100 nm$ give rise to new properties of nanostructures built from them.
Particles that are smaller than the characteristic length for a particular phenomenon show different physical and chemical properties than particles of larger sizes. For example, mechanical properties, optical properties, conductivity, melting point, and reactivity have all been observed to change when particles become smaller than the characteristic length.
Gold and silver nanoparticles were used in window glass panes to obtain a variety of beautiful colors. Nanotechnology has a wide range of applications like producing lighter but stronger materials, constructing faster switches for computers, improving drug delivery to specific organs of the body, etc.
The radii of atoms and most of the molecules are less than a nanometer. Nanoparticles are generally considered to have a radius in the range of $1 nm$ to $100 nm$ which can have $25$ to $10^{6}$ atoms. A cluster of $1 nm$ radius has approximately $25$ atoms. This definition of nanoparticles based on size does not distinguish between molecules and nanoparticles as many organic molecules contain more than $25$ atoms.
Nanoparticles can be more appropriately defined as an aggregate of atoms, with a radius between 1 nm and 100 nm, with dimensions less than the characteristic length of some physical phenomena.
When particle size is less than the characteristic length of some physical phenomena, the particles show different properties. The nanoparticles show unique properties that change with their size. Classical mechanics is able to explain the properties of bulk materials but is unable to explain the properties of nanoparticles. Quantum mechanical principles have to be used to explain the properties of the nanoparticles.
Properties of Nanoparticles
As discussed earlier, the properties of nanoparticles are different from the bulk material. The properties of nanoparticles also vary with size and shape. Hence different properties can be obtained by changing the size and shape of the nanoparticles. Some of the properties of nanoparticles are as follows :
1) Optical properties: The color of nanoparticles is different from the bulk material. When a bulk material is reduced in size to a few hundred atoms, the energy band structure of the bulk material changes to a set of discrete energy levels. Atomic clusters of different sizes will have different energy level separations. As clusters of different sizes have different energy level separations, the color of the clusters (which are due to transitions between the energy levels) will depend on their size. Hence the size of the cluster can be altered to change the colour of a material. For example, gold in bulk form appears yellow but gold nanoparticles appear bright red in color. The medieval glass makers produced tinted glass with a beautiful variety of colors by dissolving metal particles like gold, silver, cobalt, iron, etc. Due to these metal nanoparticles, the glasses appear colored.
In semiconductor nanoparticles (which are used in quantum dots) there is a significant shift in the optical absorption spectra towards blue as the particle size is reduced.
2) Electrical properties: The resistivity in bulk matter is mainly due to the scattering of electrons by ions and crystal defects. In nanostructures, the resistivity mainly depends on scattering from the boundaries of nanoparticles when particle size becomes less than the mean free path between collisions. Thus smaller particle size increases the resistivity.
Various types of defects in the lattice also increase the resistivity by limiting the mean free path. However many nanostructures are too small to have internal defects.
Another effect of reduced size is the confinement of conduction electrons. In bulk conductors, the electrons move freely throughout the entire conductor. The situation changes when one or more dimensions of the conductor are made very small.
Consider a flat conducting plate with a large length and width but a small thickness in the range of a few nanometers. In this configuration, called a quantum well, the electron will be confined along one dimension but will move freely along the remaining two dimensions.
If a conducting wire has a long length but a very small diameter, the electrons can move freely along the length but will be confined in two mutually perpendicular transverse directions. This configuration is known as a quantum wire.
If all three dimensions of the conductor are in nanometer range, the configuration is called a quantum dot and the electron is confined in all three dimensions. Confinement of electrons to small dimensions leads to quantization of energy.
The level of doping in semiconductors gives rise to another important phenomenon. For typical doping levels of 1 donor impurity atom in $10^{8}$ atoms of semiconductor atoms, a quantum dot of $10^{7}$ semiconductor atoms would have an average of $10^{-1}$ electrons. In other words, on an average, one quantum dot in 10 will have a free electron. These result in the phenomena of single-electron tunneling and coulomb blockade. The conduction is due to the tunneling of electrons through the quantum dot. The electrons are blocked from tunneling except at discrete voltage change positions. This phenomenon is called coulomb blockade. The I-V characteristic shown in the above Figure is called the coulomb staircase.
3) Magnetic properties: Magnetic properties are basically due to the orbital and spin motions of electrons around the nucleus. Every electron in an atom has spin and orbital magnetic moment which, when added, gives the total magnetic moment of the electron. The vector sum of all the moments of electrons gives the total moment of the atom. In most of the atoms, the net magnetic moment is zero.
However, atoms like iron, cobalt, and manganese, have a net magnetic moment. Crystals of these become atoms ferromagnetic when magnetic moments of all atoms are aligned in the same direction. The magnetic moment of magnetic nanoparticles is observed to be less than the value for perfect alignment of all moments. The net magnetic moment is observed to decrease with increasing temperature. This is due to thermal vibration of atoms in the cluster which disturbs the alignment of magnetic moments.
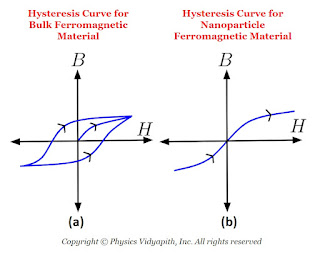
In bulk ferromagnetic materials, the magnetic moment is less than the moment the material would have if every atomic moment were aligned in the same direction. This is due to the presence of 'domains' which are regions in which all atomic moments are in one direction but moments of different domains are in different directions. When bulk ferromagnetic materials are subjected to alternating magnetic fields, they show hysteresis for which the B-H curve is shown in the above Figure (a). In nanosized ferromagnetic particles, essentially consisting of a single domain, there is no hysteresis and the $B-H$ curve is as shown in the above Figure (b). These particles are called the superparamagnetic.
The saturation magnetization is observed to increase significantly on decreasing the particle size. Another interesting property of nanoparticles is that clusters made of up nonmagnetic atoms like rhenium show magnetic moment which increases with the decrease in particle size.
4) Structural properties: The structure of small nanoparticles can be entirely different from that of the bulk material. The crystal structure of large nanoparticles is observed to be the same as the bulk material but with different lattice parameters. As a result of the changed structure, the electronic structure changes which in turn leads to changes in optical properties and reactivity. (TWD)
5) Mechanical properties: Mechanical properties like hardness, elasticity, and ductility depend upon the bonds between atoms. Imperfections in the crystal structure and impurities result in changes in these properties. As the nanoparticles are highly pure and free from imperfections, they show different mechanical properties than the bulk material. It has been observed that Young's modulus decreases in metallic nanocrystals with a decrease in particle size. The yield stress has been observed to increase with the decrease in grain size in bulk materials with nanosized grains. Hence stronger materials can be produced by making materials with nanosized grains. The carbon nanotubes are estimated to be about 20 times stronger than steel.