Description of Force and their Types

Force:

Force is a push or pull by which the state of the object changes or tends to change.

Types of forces:

There are two types of forces-

1.) Contact Force
2.) Non-Contact Force

1.) Contact force:

When there is physical contact between the two objects by push or pull then it is known as contact force.

For Example:

i.) When a coiled spring is stretched (pulled), the two ends of the spring must be in actual contact with the person's hands.
ii.) Kicking a football, and pulling a cart are also contact forces.

Types of Contact Force:

I.) Applied Force
II.) Frictional Force
III.) Normal Force
IV.) Tension Force
V.) Air Resistance (Drag Force)
VI.) Elastic or Restoring force

I.) Applied Force:

When a force is exerted by a person or an object to another person or object then this force is known as applied force.

$F=ma$

Example: Pushing a shopping cart, pulling a door open.

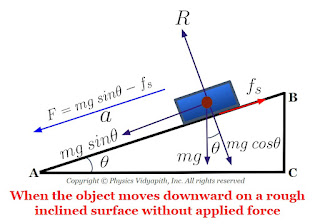
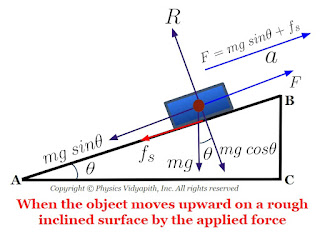
II.) Frictional Force:

When two surfaces are in motion relative to each other and in contact then a force acting in the opposite direction of the motion of one surface over the other is called the force of friction. The frictional force is also called the force of friction or simply friction.

$F=\mu R$

A smooth surface exerts a lesser force of friction than a rough surface. The rolling frictional froce is always less than the sliding frictional force.

Types of Friction Force:

i.) Static Friction:

When the frictional force is applied on the object due state of the rest of the object then frictional force is known as static friction.

ii.) Kinetic Friction:

When the frictional force is applied to the object due motion of the object then frictional force is known as dynamic friction.

iii.) Limiting Friction:

The maximum value of static frictional force is known as limiting friction.

Example: Rubbing hands together, a car’s brakes stopping a vehicle

III.) Normal Reaction Force:

When an object is placed on a surface (or another object), the object exerts a force on the surface (or another object) vertically downwards. However, the object does not move in the direction of the force. This is because the surface (or another object) exerts an equal and opposite force on the object vertically upwards. then this force is called normal reaction force.

$Normal \: reaction \: force (N) = Weight \: of \: the \: object (mg) $

Example: A book resting on a table, a person standing on the ground.

IV.) Tension force:

The force on the string, rope, or cable due to pulled tight is known as Tension. Force is transmitted through a s when pulled tight.

Example: A person pulling a rope in a tug-of-war, a hanging lightbulb.

V.) Air Resistance (Drag Force):

It is a type of friction force that acts against objects moving through the air.

Example: A parachute slowing down a skydiver, wind resistance on a car.

VI.) Spring Force (Elastic Force Or Restoring force):

A force that always acts in the opposite direction of the object's displacement is known as elastic or restoring force.

Example: A compressed spring in a toy, a rubber band being stretched.

2. Non-Contact Forces (Act at a distance)

I.) Gravitational Force (F)

The force of attraction between two heavy objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

$F=G \frac{m_{1}m_{2}}{r^{2}}$

This force is most effective between very heavy objects like satellites, Planets Su,n and Stars.

Example: Objects falling to the ground, Earth’s gravity keeping the Moon in orbit.

II.) Electromagnetic Force:

When electric force and magnetic force are applied perpendicular to each other on charged particles then a force acts perpendicular to both this force is known as electromagnetic force.

The force between charged objects include both electric force and magnetic forces.

Example: Lightning (electric force), magnets attracting iron nails.

i.) Magnetic Force:

The force between magnetic materials, either attracting or repelling is known as magnetic force. The magnitude of magnetic force due to moving charge is described by Lorentz's law ($F=qvB sin \theta$)and direction is described by Fleming's left-hand rule. Similarly, the magnetic force due to the conductor is described by the formula $F=iBl sin\theta$ that is deduced by Lorentz's law, and the direction of force in a conductor is also described by Fleming's left-hand rule.

Example: A compass needle pointing north, fridge magnets sticking to a fridge.

ii.) Electric Force:

The attraction and repulsion force between the charges is known as the electric force. The magnitude of this force is described by Coulomb's law and the direction is described by the vector form of Coulomb's Law.

$F=\frac{1}{4\pi \epsilon_{\circ} K} \frac{q_{1}q_{2}}{r^{2}}$

IV.) Nuclear Forces: The force between the nucleons (i.e. proton and neutron) is known as nuclear force. Nuclear forces are two types.

i.) Strong Nuclear Force:

It is the very strongest and short-distance force that holds protons and neutrons together in an atomic nucleus.

ii.) Weak Nuclear Force:

When the nucleus is involved in radioactive $\beta$ decay then the force between the particles is known as weak nuclear force. The force is involved in the reaction of nuclear fission and fusion.

Example: The energy released in nuclear reactions, like in the Sun or nuclear power plants.

Read more

Work energy theorem Statement and Derivation

Work-energy theorem statement:

The work between the two positions is always equal to the change in kinetic energy between these positions. This is known as the work energy Theorem.

$W=K_{f}-K_{i}$

$W=\Delta K$

Derivation of the Work-energy theorem:

According to the equation of motion:

$v^{2}_{B}=v^{2}_{A}+2as $

$2as=v^{2}_{B}-v^{2}_{A}$

$2mas=m(v^{2}_{B}-v^{2}_{A})$

$mas=\frac{m}{2} (v^{2}_{B}-v^{2}_{A})$

$Fs=\frac{1}{2}mv^{2}_{B}-\frac{1}{2}mv^{2}_{A} \qquad (\because F=ma)$

$W=\frac{1}{2}mv^{2}_{B}-\frac{1}{2}mv^{2}_{A} \qquad (\because W=Fs)$

$W=K_{f}-K_{i}$

Where
$K_{f}$= Final Kinetic Energy at position $B$
$K_{i}$= Initial Kinetic Energy at position $A$

$W=\Delta K$

Alternative Method (Integration Method):

We know that the work done by force on a particle from position $A$ to position $B$ is-

$W=\int F ds$

$W=\int (ma)ds \qquad (\because F=ma)$

$W=m \int \frac{dv}{dt}ds$

$W=m \int dv \frac{ds}{dt}$

$W=m \int v dv \qquad (\because v=\frac{ds}{dt})$

If position $A$ is the initial point where velocity is $v_{A}$ and position $B$ is the final point where velocity is $v_{B}$ then work is done by force under the limit-

$W=m \int_{v_{A}}^{v_{B}} v dv$

$W=m[\frac{v^{2}}{2}]_{v_{A}}^{v_{B}} $

$W=\frac{1}{2}mv^{2}_{B}-\frac{1}{2}mv^{2}_{A}$

$W=K_{f}-K_{i}$

$W=\Delta {K}$

Read more

Force of Friction | Expression for the acceleration and the work done on inclined rough surface| Advantage and Disadvantage

Definition of Friction:

When an object slides over the surface of another object then each surface applies a parallel force to the other. This force is called friction force. The direction of the force of friction on every object with respect to the other is always opposite to the motion of the second object.

$F=\mu R$

Properties of Friction Force:

The force of friction always acts in the opposite direction of the motion of the object.

The force of friction always opposes the motion of the object. So it does not help in motion.

Friction force always helps an object to be in the rest of the position. i.e If an object is in the rest of the position that is due to only frictional force.

The frictional force is act on both states of the object i.e Rest and motion.

Modern Concept of Friction:

It is now believed that frictional forces arise because of a fundamental force occurring in nature commonly known as an electric force. Every object has surface irregularities at the atomic level.

When two surfaces come in contact then the real area in contact is much smaller than the actual area of the surface. At the contact points, the distance between the particles becomes very small and as such the molecular electrical forces begin to act between the surfaces and molecular bonds are formed.

When one of the surfaces is pulled over the other, the molecular bonds are broken. As a result, the material of the objects is deformed and new bonds are formed. The successive loading and deformation processes result in loss of energy which appears in the form of heat. To compensate for the energy loss, a force is required to be applied to start the motion.

Types of forces of friction: There are two types of forces of friction

1. Force of Static Friction
2. Force of Dynamic Friction

1. Force of Static Friction:

When the friction forces acting between two surfaces at rest with respect to each other are called the force of static friction.

Note: The maximum value of the force of static friction is always equal to the minimum value of force required to start the motion. Once the motion starts, the force of friction after reducing becomes such that it is sufficient to maintain uniform motion.

Due to the force of static friction between two dry and unlubricator surfaces, the maximum force is according to the following two laws:

i.) The maximum force does not normally depend upon the area of contact.
ii.) It is directly proportional to the normal reaction.

Coefficient of Static Friction:

The ratio of the maximum value of force in static friction and normal reaction is called the coefficient of static friction.

$\mu_{s}=\frac{F}{R}$

2. Force of Dynamic Friction:

When the force of friction acting between the two surfaces in relative motion is called the force of dynamic friction.

Note: Due to dynamic friction between the dry and unlubricated surfaces the value of dynamic friction is according to the two laws:

i.) It does not depend upon the surfaces of contact.
ii.) It is equal to the maximum normal reaction force.

Coefficient of Dynamic Friction:

The ratio of force in dynamic friction and normal reaction is called the coefficient of dynamic friction.

$\mu_{k}=\frac{F}{R}$

Limiting friction:

It is the maximum value of friction that acts when the object just begins to move is called Limiting Friction. The limiting friction is directly proportional to the normal reaction in the object. i.e

$F \propto R$

$F = \mu R$

Angle of friction:

The angle between the effective resistance $S$ (i.e resultant of frictional force and normal reaction) and normal reaction $R$ is called the angle of friction.

Let us consider, A object of mass $m$ placed on a horizontal surface. If $F$ force is applied on the object then the value of limiting friction

$F \propto R$

$F = \mu R$

$\mu=\frac{F}{R} \qquad(1.1)$

From figure in $\Delta ROS$

$tan \theta =\frac{RS}{RO}$

$tan \theta =\frac{RS}{RO}$

$tan \theta =\frac{F}{R} \qquad \left( \because RS=F \: and \: RO=R \right)$

From the equation $(1.1)$ and the above equation, We can conclude that

$\mu=tan\theta$

Angle of Repose and Angle of Sliding:

The angle of repose or angle of sliding is defined as the minimum angle of inclination of a surface with the horizontal, such that an object placed on the surface just begins to slide down.

The various forces acting on the object are shown in the figure below:

i.) Weight $mg$ of the object acting vertically downwards.
ii.) Normal Reaction $R$ acting perpendicular to inclined surface $AB$
iii.) Force of friction $f$ acting up in the inclined surface $AB$

Now from the figure apply the equilibrium condition:

$R=mg \: cos\theta \qquad(1.2)$

$f=mg \: sin\theta \qquad(1.3)$

Now divide by equation $(1.3)$ to equation $(1.2)$

$\frac{f}{R}=\frac{mg \: sin\theta}{mg \: cos\theta}$

$\frac{f}{R}=\frac{sin\theta}{cos\theta}$

$\frac{f}{R}=tan \theta$

$\frac{\mu R}{R}=tan \theta \qquad \left( \because f=\mu R \right)$

$\mu =tan \theta $

Thus the angle of friction is equal to the angle of repose.

1.) Expression for the acceleration and work done on the object moves downward on a rough inclined surface without applied force:

Let us consider, A object of mass $m$ moving sliding downward on a rough surface that is inclined at an angle $\theta$ from horizontal. If the angle $\theta$ of the inclined surface is greater than the angle of repose, the object slides down with an acceleration $a$ without any applied force.

The various forces acting on the object are shown in the figure below:

i.) Weight $mg$ of the object acting vertically downwards.
ii.) Normal Reaction $R$ acting perpendicular to inclined surface $AB$
iii.) Force of friction $f$ acting up in the inclined surface $AB$

Apply the equilibrium condition from the figure:

$R=mg \: cos\theta \qquad(1.4)$

The net force on the object moving down the inclined surface

$F=mg \: sin\theta - f \qquad(1.5)$

$F=mg \: sin\theta - \mu R $

Now substitute the value of $R$ from equation $(1.4)$ in above equation

$F=mg \: sin\theta - \mu mg \: sin \theta$

$ma=mg \left( \: sin\theta - \mu \: sin \theta \right) \qquad( F=ma)$

$a=g \left( \: sin\theta - \mu \: sin \theta \right) $

If the object is displaced the distance $S$ by the acceleration $a$ then work done by force:

$W=F.S$

$W= mg \left(\: sin\theta - \mu \: sin \theta \right). S$

2.) Expression for acceleration and work done on the object moving upward on a rough inclined surface by the applied force:

Let us consider, A object of mass $m$ moving upward on a rough inclined surface by applying the force $F$ sliding downward on a rough surface so the various forces acting on the object are shown in the figure below:

i.) Weight $mg$ of the object acting vertically downwards.
ii.) Normal Reaction $R$ acting perpendicular to inclined surface $AB$
iii.) Force of friction $f$ acting up in the inclined surface $AB$

In equilibrium condition from the figure:

$R=mg \: cos\theta \qquad(1.6)$

The net force on the object moving down the inclined surface

$F=mg \: sin\theta + f \qquad(1.7)$

$F=mg \: sin\theta + \mu R $

Now substitute the value of $R$ from equation $(1.6)$ in above equation

$F=mg \: sin\theta + \mu mg \: sin \theta$

$ma=mg \left( \: sin\theta + \mu \: sin \theta \right) \qquad( \because F=ma)$

$a=g \left( \: sin\theta + \mu \: sin \theta \right) $

If the object is displaced the distance $S$ by the force $F$ then work done by force:

$W=F.S$

$W= mg \left(\: sin\theta + \mu \: sin \theta \right). S$

3.) Expression for acceleration and work done on the object moves on a rough horizontal surface by the applied force:

Let us consider, A object is moving on a rough horizontal surface by applying the force $F$ on the object of mass $m$ and then the net force on the object from the figure below

$F-f=ma$

$F-\mu R=ma \qquad \left(\because f=\mu R \right)$

$F-\mu mg=ma \qquad \left(R=mg \right)$

$F=m \left(\mu g+a \right)$

$a=\frac{F-\mu mg}{m}$

If the object is displaced the distance $S$ by the force $F$ then work done by force:

$W=F.S$

$W= m \left(\mu g+a \right). S$

The Advantages of Friction:

The two objects will not stick to each other if there is no friction between the surface.

The parts of machinery are held together with the help of nuts and bolts but without friction, these can not be held.

A person can not walk or stand on the surface without friction.

The brakes of any vehicle will not work without friction.

It is not possible to transfer motion from one part of a machine to the other part without the help of friction.

Sandpaper is used in cleaning because this cleaning is only possible with the help of friction.

Adhesives will lose their purpose.

The Disadvantage of Friction:

Friction always opposes the relative motion between any two objects in contact. Therefore, extra energy is lost to overcome friction. Thus, friction involves the unnecessary loss of energy. This shows that the output is always less than the input.

Friction between the parts of machinery causes wears and tear. Therefore, the lifetime of the parts of the machinery reduces.

Frictional forces produce heat, which causes damage to the machinery.

Methods of Reducing friction:

By Polishing: Polishing makes the surface smoother. Therefore, friction reduces.

By Streamlining: Friction due t air is considerably reduced by streamlining the shape of the object (sharp in front) moving through the air.

By Lubrication: Oil, grease, and many other materials are used as lubricants. These lubricants fill up the irregularities of the surface making them smother. Hence, friction decreases.

By proper selection of materials.

By using ball bearings.

Read more

Motion of body in a vertical circle and its Practical Applications

Calculation of Motion of a body in a vertical Circle: Let us consider, A body that has mass $m$ moving in a vertical circle of radius $r$. If at any instant the body is at position $P$ with angular displacement $\theta$ from the lower position $L$ of the circle. As shown in the figure below.

The various forces acting on the body are:

The weight $mg$ of the body, acting vertically downwards

Tension $T$in the string acting along the $PO$. Now $mg$ can be resolved into two components:

1.) The horizontal component $mg cos\theta$ opposite to $T$

2.) The vertical component $mg sin\theta$ act along tangent to the circle at $P$

So the net force on the body at position $P$ provides the necessary centripetal force required by the body

$T-mg cos\theta = \frac{m v^{2}}{r}$

$T= \frac{m v^{2}}{r} + mg \: cos\theta \qquad(1)$

Tension and velocity at the highest position $H$ of the verticle circle: At the highest position $H$ the tension $T_{H}$ of the will be minimum and the velocity $v_{H}$ will also be minimum.

If $cos\theta = -1$ i.e. $\theta=180^{\circ}$

Then Tension $T$ and velocity $v$ will be minimum i.e $T_{H}$ and $v_{H}$

so from equation $(1)$

$T_{H}= \frac{m v_{H}^{2}}{r} - mg $

So from the above equation, we can conclude that The body will move along the vertical circle only when $T_{H} \geq 0$

$\left( \frac{m v_{H}^{2}}{r} - mg \right) \geq 0$

$ \frac{m v_{H}^{2}}{r} \geq mg $

$ \frac{ v_{H}^{2}}{r} \geq g $

$ v_{H} \geq \sqrt {rg} $

Thus the minimum value of the velocity at the highest position is $\sqrt{rg}$

Tension and velocity at lowest position $L$ of the verticle circle: At the lowest position $L$ the tension and velocity will be maximum. Now applying the principle of energy conservation for the position $H$ and $L$ of the body.

Total energy at $L$ =Total energy at $H$

$\frac{1}{2}m v_{L}^{2}=\frac{1}{2}m v_{H}^{2} +mg(2r)$

Now substitute the value of $v_{H} \geq \sqrt{gr}$ in above equation then we get

$\frac{1}{2}m v_{L}^{2}=\frac{1}{2}m (gr) +mg(2r)$

$\frac{1}{2}m v_{L}^{2}=\frac{5mgr}{2}$

$v_{L} \geq \sqrt{5gr}$

For the maximum value of tension $T_{L}$ at the lowest position $L$ of the vertical circle. Now put $cos \theta =1$ i.e $\theta=0^{\circ}$ in the equation $(1)$ then we get

$T_{L}= \frac{m v_{L}^{2}}{r} + mg $

Now substitute the value of $v_{L} \geq \sqrt{5gr}$ in the above equation then

$T_{L} \geq \frac{m 5gr}{r} + mg $

$T_{L} \geq 6gr$

Tension and velocity at horizontal position $M$ of the verticle circle:

Now apply the principle of conservation of energy for position $M$ and position $L$

Total energy at $M$ =Total energy at $L$

$ \frac{1}{2}m v_{M}^{2} + mgr = \frac{1}{2} m v_{L}^{2}$

$ \frac{1}{2}m v_{M}^{2} = \frac{1}{2} m v_{L}^{2} - mgr$

Now substitute the value of $v_{L} \geq \sqrt{5gr}$ in the above equation then

$ \frac{1}{2}m v_{M}^{2} \geq \frac{1}{2} m 5gr - mgr$

$ \frac{1}{2}m v_{M}^{2} \geq \frac{3 mgr}{2}$

$v_{M}^{2} \geq 3 gr$

$v_{M} \geq \sqrt{3 gr}$

To find the tension $T_{M}$ at position $M$ substitute the $cos \theta =0$ i.e $\theta =90^{\circ}$ in equation $(1)$. Then we get

$T_{M} = \frac{m v_{M}^{2}}{r} + 0$

$T_{M} = \frac{m v_{M}^{2}}{r}$

Now substitute the value of $v_{M} \geq \sqrt{3gr}$ in the above equation. Then we get

$T_{M} \geq 3mg$

Practical Application of motion in a vertical Circle:

1.) When a bucket containing water is rotated in a vertical circle with a velocity at the lowest point $v_{L} \geq \sqrt{5gr}$, water shall not spill even at the highest point, when the bucket is upside down. If the bucket is whirled slowly, so that $ \left(mg \gt \frac{mv_{H}^{2}}{r} \right) $, then a part of the weight shall provide the necessary centripetal force $\left( \frac{mv_{H}^{2}}{r} \right)$; and the rest of the weight of water $\left( mg - \frac{mv_{H}^{2}}{r} \right) $ causes some water to accelerate downwards and spill. Only this much water shall leave the bucket.

2.) A pilot of an aircraft can successfully loop a vertical loop without falling at the top of the loop (being without a belt) when its velocity at the bottom of the loop is $\geq \sqrt{5gr}$

3.) In a circus, a motorcyclist is able to perform the feat of driving the motorcycle along a vertical circle in a cage. The motorcyclist does not fall even at the highest point, when his velocity at the bottom of the cage is $\geq \sqrt{5gr}$.

To acquire this velocity at the lowest point $L$ of the vertical circle of radius $r$, he has to roll down a vertical height $h$, As shown in the figure below:

From the equation of motion $v^{2}=u^{2}+2as$

Let $u=0$, $a=+g$ and $s=h$

we get, $v^{2}=0 +2gh$

$v=\sqrt{2gh}$

To move in a vertical circle, the velocity $v$ acquired at $L$ must at least be equal to $\sqrt{5gr}$. i.e.

$\sqrt{2gh}= \sqrt{5gr}$

$h=\frac{5r}{2}$

Read more

Definition of work done and its essential condition

Work: When a force is applied on a body and a body is displaced along the line of action of force then this is called the work done by force. Work is a scalar quantity.

Unit: $Joule$, $N-m$

Dimension: $[ML^{2}T^{-2}]$

Example: When a boy kicks a football to move it, the boy is said to have done some work.

Let us consider, A body that has mass $m$. If a force $F$ applied on a body at an angle $\theta$ and body is displaced from position $A$ to position $B$ with distance $d$ then work done by force:

$W= horizontal \: component \: of \: the \: force \times displacement $

$W=F\:cos\theta \times d$

$W=F d\:cos\theta \qquad(1)$

$W=\overrightarrow{F}. \overrightarrow{d}$

So, we can conclude from the above equation that "The work done by the force is the scalar product of the force and displacement ".

Note: When the force is applied at an angle $\theta$ then the vertical component of the force is balanced by weight $mg$ and the horizontal component of the force is responsible for the motion of the body.

Essential Condition for work to be done:

For work to be done, the following two conditions should be satisfied

A force should act on the body.

The body should move in the direction of the force, or opposite to it, i.e the point of application of the force should move in the direction of the force or opposite to it. In other words, the body must be displaced

Types of Work done by force:

Positive Work done

Zero Work done

Negative Work done

Positive Work done: When a force is applied on a body and the body is displaced along in direction of the force then this is called the positive work done by force.

If $\theta=0 ^{\circ}$, then $cos0 ^{\circ} =1$

the from equation $(1)$

So Work done by force

$W=Fd$

Zero Work done: When a force is applied on a body and the body is not displaced from its position then this is called the zero work done by force.

If $\theta=90 ^{\circ}$, then $cos90 ^{\circ} =0$

then from equation $(1)$

So Work done by force

$W=0$

Negative Work done: When a force is applied on the body and a body is displaced along in the opposite direction of the force then this is called the negative work done by force.

If $\theta=180^{\circ}$, then $cos 0^{\circ} =-1$

then from equation $(1)$

So Work done by force

$W=-Fd$

** 1 Joule Work done: When $1 \: Newton$ of force is applied on a body and a body is displaced by $1\: m$ along the line of action of force then this is called the $1 \: Joule$ work done by force.**

Read more

Principle and Proof of Law of Conservation of Energy

Law of Conservation of Energy: According to this principle

The energy is neither created nor destroyed. The energy can be changed from one form to another form. i.e. when there is not any external influence is applied on the particle then the total energy of the particle is always conserved.

Proof of Conservation's Law of Energy: Let us consider, A particle is freely falling from height $h$ under the gravitational acceleration $g$. So the total energy of the particle at different points :

Calculation of Total Energy at Point $A$:

The initial velocity of the particle at point $A$ is $(v_{A})=0$

The kinetic energy of the particle at point $A$ is $(K_{A})=\frac{1}{2}mv_{A}^{2}$

$K_{A}=0\qquad \left( \because v_{A}=0 \right)$

The potential energy of the particle at point $A$ is $(U_{A})=mgh$

The total energy of a particle at point $A$ is $(E_{A})=K_{A}+U_{A}$

Now substitute the value of $K_{A}$ and $U_{A}$ in the above equation. Now the above equation can be written as:

$E_{A}=0+mgh$

$E_{A}=mgh \qquad(1)$

Calculation of Total Energy at Point $B$: If a particle travels the distance $x$ and reaches point $B$ then velocity at point $B$ can be calculated by the equation of motion. i.e.

$v_{B}^{2}=v_{A}^{2}+2gx$

But the initial velocity of the particle is zero. i.e $v_{A}=0$ then the above equation can be written as

$v_{B}^{2}=0+2gx$

$v_{B}^{2}=2gx$

The kinetic energy of the particle at point $B$ is $(K_{B})=\frac{1}{2}mv_{B}^{2}$

Now substitute the value of $v_{B}^{2}$ in the above equation. Now the above equation can be written as:

$K_{B}=\frac{1}{2}m \left( 2g x \right)$

$K_{B}=mgx $

The height of the particle at point $B$ is $(h-x)$ then the potential energy at point $B$ is $(U_{B})=mg(h-x)$

The total energy of a particle at point $B$ is $(E_{B})=K_{B}+U_{B}$

Now substitute the value of $K_{B}$ and $U_{B}$ in the above equation. Now the above equation can be written as:

$E_{B}=mgx+mg(h-x)$

$E_{B}=mgh \qquad(2)$

Calculation of Total Energy at Point $C$: Now the particle reaches point $C$ by traveling distance $h$ from the initial point $A$. This point $C$ is just before the collision from the surface. So the velocity of the particle at point $C$.

$v_{C}^{2}= v_{A}^{2}+2gh$

$v_{C}^{2}= 0+2gh \qquad \left( v_{A}=0 \right)$

$v_{C}^{2}= 2gh$

The kinetic energy of the particle at point $C$ is $(K_{C})=\frac{1}{2}mv_{C}^{2}$

Now substitute the value of $v_{C}^{2}$ in the above equation. Now the above equation can be written as:

$K_{C}=\frac{1}{2}(2mgh)$

$K_{C}=mgh$

At point $C$ the particle is just above the surface so the height $h$ of the object will be zero. i.e. $h=0$

The potential energy at point $C$ is $(U_{C})=0$

The total energy of the particle at point $C$ is $(E_{C})=K_{C}+U_{C}$

Now substitute the value of $K_{C}$ and $U_{C}$ in the above equation. Now the above equation can be written as:

$E_{C}=mgh+0$

$E_{C}=mgh \qquad(3)$

From the above equation $(1)$, equation $(2)$ and equation $(3)$, we get

$E_{A}=E_{B}=E_{C}$

Now we can conclude that the total energy of the particle is always conserved when there is no external influence applied. This is proof of the law of conservation of Energy.

Read more

Definition and Practical Applications of Centripetal Force

Definition of Centripetal Force:

When a particle moves in a circular path then a force act, toward the centre of the circle, on a particle. This type of force is called the centripetal force.

This force is also known as a radial force because the direction of force is toward the centre of the circle.

Let us consider, A particle of mass $m$ moving around a circular path of radius $r$ with linear velocity $v$. So the force on a particle:

$F=ma$

Where $a$ is centripetal acceleration i.e. $a=\frac{v^{2}}{r}$. So the force on a particle can be written as

$F=m\frac{v^{2}}{r}$

$F=\frac{mv^{2}}{r}$

$F=m\frac{(r \omega)^{2}}{r} \qquad \left( \because v=r \omega \right)$

$F=mr\omega^{2}$

$F=mr\left(\frac{2\pi}{T}\right)^{2} \qquad \left( \because \omega=\frac{2\pi}{T} \right)$

$F=mr\frac{4\pi^{2}}{T^{2}}$

$F= \frac{4 \pi^{2} m r}{T^{2}} $

$F=4 \pi^{2} m r n^{2} \qquad \left( \because n=\frac{1}{T} \right)$

Practical Applications of Centripetal Force:

1. The planets revolve around the sun and the necessary centripetal force is achieved by gravitational force between the sun and the planet. as shown in the figure below

2. The electrons revolve around the nucleus of the atom and the necessary centripetal force is achieved by the force of attraction on the revolving electrons and protons in the nucleus. as shown in the figure below

3. In this case, When a piece of stone is tied to the end of a string whose other end is held in the hand then the required centripetal force, to revolve the stone in a circular path, is achieved by the tension of the string.

4. When a motor car is moving in a curved path then the necessary centripetal force is achieved by friction between the wheels and the road.

5. Rounding a Level Curve Road: When a vehicle goes in round a curved road, it requires some centripetal force. While rounding the curve, the wheels of the vehicle have a tendency to leave the curved path and regain the straight line path. The force of friction between the wheels and the road opposes this tendency of the wheels. This frictional force acts towards the centre of the circular track and provides the required centripetal force.

The forces acting on moving vehicles on the curved road are

Weight $mg$ of the vehicle act vertically downward

Normal reaction $R_{1}$ and $R_{2}$ from both sides of the wheels act vertically upward from the horizontal surface

The frictional force $F_{1}$ and $F_{2}$ from both sides of wheels of the vehicle

Hence, the centripetal force is provided by friction force only, therefore

$\frac{mv^{2}}{r} \leq F_{1}+F_{2}$

Where $F_{1}=\mu R_{1}$ and $F_{2}=\mu R_{2}$, then

$\frac{mv^{2}}{r} \leq \mu R_{1}+\mu R_{2}$

$\frac{mv^{2}}{r} \leq \mu \left( R_{1}+ R_{2} \right)$

$\frac{mv^{2}}{r} \leq \mu R \qquad \left( R= R_{1}+ R_{2} \right)$

$\frac{mv^{2}}{r} \leq \mu mg \qquad \left(R=mg \right)$

$\frac{v^{2}}{r} \leq \mu g $

$v^{2} \leq \mu r g$

$v \leq \sqrt{\mu r g}$

Here, $\mu$ is the frictional coefficient.

This is the maximum velocity of the vehicle for rounding on a level curved road without sliding. But the value is very low as it depends on the friction coefficient.

6. Banking of roads: The phenomenon of raising the outer age of the curved road above the inner age is called the banking of roads. When a vehicle moves on the curved path at a reasonable speed without slipping then sufficient centripetal force is required to move in a curved path which is achieved by banking of the road.

In the case of the Banking of roads, The centripetal force is not provided by friction between the wheels and the road.

Calculation of the angle of banking:

Let us consider, A vehicle of mass $m$ moving around the curved path of radius $r$ with velocity $v$ on a road banking through an angle $\theta$. The forces applying to the vehicle are:

A.) The weight $mg$ act vertically downward.

B.) Normal reaction $R$ of the ground acts perpendicular to the banked road and can be resolved into two components. i.e. Verticle component $R sin\theta$ and Horizontal component $R cos\theta$.

C.) The horizontal component $R cos\theta$ is balanced by the weight $mg$ of the vehicle. i.e.

$R cos\theta= mg \qquad (1)$.

D.) The vertical component of normal reaction $R sin\theta$ acts along the horizontal towards the centre of the circular path and it provides the centripetal force. i.e.

$R sin\theta=\frac{mv^{2}}{r} \qquad (2)$

Now divide equation $(2)$ and equation $(1)$

$\frac{R sin\theta}{R cos\theta}= \frac{\frac{mv^{2}}{r}}{mg}$

$\frac{ sin\theta}{ cos\theta}=\frac{v^{2}}{rg} $

$ tan\theta=\frac{v^{2}}{rg} \qquad(3)$

$ \theta=tan ^{-1} \left( \frac{v^{2}}{gr} \right)$

If $h$ is the height $AB$ of the outer edge of the road above the inner edge and $b$ is the breadth $OB$ of the road then from the figure:

$OA=\sqrt {(OB)^{2}-(AB)^{2}}$

$OA=\sqrt {b^{2}-h^{2}}$

$tan\theta=\frac{AB}{OA}$

$tan\theta=\frac{h}{\sqrt {b^{2}-h^{2}}} \qquad (4)$

From equation $(3)$ and equation $(4)$

$tan\theta=\frac{v^{2}}{rg}=\frac{h}{\sqrt {b^{2}-h^{2}}}$

From the above equation, we can calculate $h$. Usually $h << b$. Therefore, $h^{2}$ is negligibly small compared to $b^{2}$. The above equation can be written as:

$tan\theta=\frac{v^{2}}{rg}=\frac{h}{b}$

Roads are usually banked for the average speed of the vehicle passing over them. However, If the speed of a vehicle is somewhat less or more than this, the self-adjusting static friction will operate between the tyres and the road, and the Vehicle will not skid.

7. Bending of Cyclist: When a cyclist takes a turn on the curved path then the cyclist has to bend the cycle a little inwards from his vertical position to achieve the necessary centripetal force.

Calculation of the angle of bending:

Let us consider, The cyclist of mass $m$ moving around the curved path of radius $r$ with velocity $V$. The force acting on the cyclist:

A.) The weight $mg$ act vertically downward.

B.) Normal reaction $R$ of the ground act on the cyclist at an angle $\theta$ with the verticle and can be resolved into two components. i.e. Verticle component $R sin\theta$ and Horizontal component $R cos\theta$.

C.) The horizontal component $R cos\theta$ is balanced by the weight $mg$ of the cyclist. i.e.

$R cos\theta= mg \qquad (1)$.

D.) The vertical component $R sin\theta$ acts along the horizontal towards the centre of the circular path and it provides the centripetal force. i.e.

$R sin\theta=\frac{mv^{2}}{r} \qquad (2)$

Now divide equation $(2)$ and equation $(1)$

$\frac{R sin\theta}{R cos\theta}= \frac{\frac{mv^{2}}{r}}{mg}$

$\frac{ sin\theta}{ cos\theta}=\frac{v^{2}}{gr}$

$ tan\theta=\frac{v^{2}}{gr}$

$ \theta=tan ^{-1} \left( \frac{v^{2}}{gr} \right)$

Read more

Definition and Derivation of Centripetal Acceleration

Definition:

When a particle moves in a circular path then acceleration act on the particle which has a direction toward the center of the circle. This acceleration is called centripetal acceleration.

Derivation of Centripetal Acceleration: Let us consider, A particle that has mass $m$ moving with velocity $v$ in a circular path of radius $r$.

If a particle is moving from point $P_{1}$ to point $P_{2}$ by covering distance $\Delta s$ on the circumference of the circle by making an angular displacement of $\theta$ at the center $O$ of the circle. The direction of velocity of the particle at point $P_{1}$ and $P_{2}$ is $\overrightarrow{v_{1}}$ and $v_{2}$.

Now take the change in velocity from point $P_{1}$ to $P_{2}$ by vector subtraction method as shown in figure below:

To find the expression for the centripetal acceleration, Now take two similar triangles $\Delta OP_{1}P_{2}$ and $\Delta ABC$ from the figure:

$\frac{OP_{1}}{AB}=\frac{P_{1}P_{2}}{BC}$

Now substitute the values from the figure in the above equation i.e.

$\frac{r}{v}=\frac{\Delta s}{\Delta v}$

$\Delta v = \frac{v}{r} \Delta s $

Now divide by $\Delta t$ into both sides the above equation can be written as

$\frac{\Delta v}{\Delta t}=\frac{v}{r} \frac{\Delta s}{\Delta t}$

If $\Delta t$ is tends to zero i.e. $\Delta t \rightarrow 0$ then

$\underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta v}{\Delta t}=\frac{v}{r} \: \underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta s}{\Delta t}$

Where
$\underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta v}{\Delta t} \rightarrow$ Instantaneous Acceleration. It is also known as Centripetal Acceleration $(a)$

$\underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta s}{\Delta t} \rightarrow$ Instantaneous Velocity $(v)$

Now the above equation can be written as

$a = \frac{v^{2}}{r} $

$a = \frac{(r\omega)^{2}}{r} \quad \left( \because v=r\omega \right)$

$a = r \omega ^{2} $

Read more

Relation between angular acceleration and linear acceleration

Derivation of equation of the relation between linear acceleration and angular acceleration:

Deduce the equation from the General form

Deduce the equation from the Differential form

We know that angular acceleration is $\alpha=\frac{\Delta \omega}{\Delta t} \qquad (1)$ $\alpha=\frac{\Delta (v/r)}{\Delta t} \qquad \left( \because \omega=\frac{v}{r} \right)$ $\alpha=\frac{1}{r} \frac{\Delta v}{\Delta t}$ If $\Delta t \rightarrow 0$ then the above equation can be written as $\alpha=\frac{1}{r} \: \underset{\Delta t \rightarrow 0}{Lim} \frac{\Delta v}{\Delta t}$ Where $\underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta v}{\Delta t}$ = Instantaneous Acceleration $(a)$ $\alpha=\frac{a}{r}$

We know that angular acceleration is $\alpha=\frac{d \omega}{dt} \qquad (1)$ $\alpha=\frac{d (v/r)}{dt} \qquad \left( \because \omega=\frac{v}{r} \right)$ $\alpha=\frac{1}{r} \frac{dv}{dt} \qquad (2)$ Where $\frac{dv}{dt}$ = Instantaneous Acceleration $(a)$ Now equation $(2)$ can be written as $\alpha=\frac{a}{r}$

Read more

Relation between angular velocity and linear velocity

Relation between angular velocity $(\omega)$ and linear velocity$(v)$: We know that the angular displacement of the particle is

$\Delta \theta= \frac{\Delta s}{r} \qquad(1)$

Where $r$ = The radius of a circle.

Now divide by $\Delta t$ on both side of equation $(1)$

$\frac{\Delta \theta}{\Delta t}=\frac{1}{r} \frac{\Delta s}{\Delta t} $

If $\Delta t \rightarrow 0$ then the above equation can be written as

$\underset{\Delta t \rightarrow 0}{Lim}\: \frac{\Delta \theta}{\Delta t}=\frac{1}{r}\: \underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta s}{\Delta t} \qquad(2)$

Where
$\underset{\Delta t \rightarrow 0}{Lim}\: \frac{\Delta \theta}{\Delta t}$ = Instantaneous Angular Velocity $(\omega)$

$\underset{\Delta t \rightarrow 0}{Lim} \: \frac{\Delta s}{\Delta t}$= Instantaneous Linear Velocity $(v)$

Now equation $(2)$ can be written as

$\omega=\frac{1}{r}v$

$v=r\omega$

This is the relation between linear velocity and angular velocity.

Read more

Conservation's Law of linear momentum and its Derivation

Derivation of Conservation's law of Linear momentum from Newton's Second Law and Statement: Let us consider, A particle that has mass $m$ and is moving with velocity $v$ then According to Newton's second law the applied force on a particle is

Derivation From General Form	Derivation from Differential Form
$F=ma$ $F=m \frac{\Delta v}{\Delta t}$ $F= \frac{\Delta (mv)}{\Delta t}$ $F= \frac{\Delta P}{\Delta t} \qquad \left( \because P=mv \right)$ If the applied force on a body is zero then $\frac{\Delta P}{\Delta t}=0$ $\Delta P=0$ Here $\Delta P$ is change in momentum of the particle .i.e $P_{2}-P_{1}=0$ $P_{2}=P_{1}$ $P=Constant$	$F=ma$ $F=m \frac{dv}{dt}$ $F= \frac{dmv}{dt}$ $F= \frac{dP}{dt} \qquad \left( \because P=mv \right)$ If the applied force on a body is zero then $\frac{dP}{dt}=0$ $dP=0$ On integrating the above equation $P=constant$

From the above equation, we conclude the statement i.e.

When no external force is applied to a particle, the total momentum of a particle is always conserved.

Derivation of Conservation's law of Linear momentum from Newton's Third Law and Statement: Let us consider, The two-particle that have mass $m_{1}$ and $m_{2}$ are moving towards each other. If

The velocity of the particles $m_{1}$ before collision is = $u_{1}$

The velocity of the particles $m_{2}$ before collision is = $u_{2}$

The velocity of the particles $m_{1}$ after collision is = $v_{1}$

The velocity of the particles $m_{2}$ after the collision is = $v_{2}$

When these particles collide to each other than according to Newton's third law

$F_{12}=-F_{21}$

$m_{1}a_{1}=m_{2}a_{2}$

$m_{1}\frac{\Delta V_{1}}{\Delta t}=m_{2} \frac{\Delta V_{2}}{\Delta t} \quad (1) \qquad \left(\because a=\frac{\Delta V} {\Delta t} \right)$

Where
$\Delta V_{1}$= Change in Velocity of mass $m_{1}$ i.e $\left( v_{1}-u_{1} \right)$
$\Delta V_{2}$= Change in Velocity of mass $m_{2}$ i.e $\left( v_{2}-u_{2} \right)$

So from equation $(1)$

$m_{1}\frac{\left( v_{1}-u_{1} \right)}{\Delta t}=m_{2} \frac{\left( v_{2}-u_{2} \right)}{\Delta t}$

$m_{1}\left( v_{1}-u_{1} \right)=m_{2} \left( v_{2}-u_{2} \right)$

$m_{1} v_{1}- m_{1} u_{1}=m_{2}v_{2}- m_{2} u_{2}$

$m_{1} u_{1}+ m_{2} u_{2}=m_{1}v_{1} + m_{2} v_{2}$

From the above equation, we conclude the statement i.e.

When two particle collide two each other. If the total momentum of the particles before the collision and total momentum of the particles after is collision is same then it is known as conservation law of linear momentum.

Read more

Conservative force and non conservative force

Conservative force: There are the following points that describe the conservative force-

1. The conservative force depends on the position of the particle and does not depend on the path of the particle.
2. In conservative force, The kinetic energy of the particle does not change between the positions.
   
   Let us consider a particle is moving from position $A$ to position $B$ under the conservative force. If the kinetic energy of the particle at position $A$ and $B$ is $K_{i}$ and $K_{f}$ then for conservative force-
   
   
   $K_{i}=K_{f}$


3. In conservative force, The work done by the force in completing one round between any two positions is zero.
   
   
   According to the work-energy theorem
   
   
   $W=\Delta{K}$
   
   
   $W=K_{f}-K_{i}.......(1)$
   
   
   For conservative force, the kinetic energy of the particle does not change between the positions of the particle. i.e.$K_{f}=K_{i}$. So from equation $(1)$
   
   
   $W=0$
   
   
   Alternative Method:
   
   
   The above statement can also be proven by the following method-
   
   
   The work is done by the force to move a particle from position $A$ to position $B$ = $W_{AB}$.
   
   
   The work done by the force to move a particle from position $B$ to position $A$ = $W_{BA}$
   
   
   We know that the kinetic of the particle does not change between the positions so work done by force between the positions will be equal and opposite. i.e
   
   
   $W_{AB}=-W_{BA}$
   
   
   $W_{AB}+W_{BA}=0$
   
   
   So from above, we can conclude that the net work done by force between the two positions in completing the one round is zero.
4. The central force is also known as the conservative force.
5. The conservative force is always equal to the negative gradient of potential energy.
   
   
   $\overrightarrow{F}=-\overrightarrow{\nabla}U$
   
   
   $\overrightarrow{F}= -\frac{dU}{dr}$

Non-conservative force:

1. The non-conservative force depends on the path of the particle between the two positions and does not depend on the positions of the particle.
2. The kinetic energy of the particle is not the same at different positions. i.e. the kinetic energy is different at different positions. The change in kinetic energy happens due to friction.
3. For non-conservative force, the work done by the force in completing one round between two positions is not zero.
4. This is not a central force.
5. The non-conservative force does not equal the negative gradient of potential energy.

Read more