Derivation→
Let us consider, A circular loop which have radius $a$, carrying a current $i$. Let take a point $P$ on the axis of the loop at a distance $x$ from the center $O$ of the loop.
Now to find the magnetic field at point $P$, take a small current element of length $dl$ at the top of the loop. Let $r$ is the distance between the current element and point $P$. Now apply the Biot-Savart's Law to find the magnitude of the magnetic field due to small current-element $dl$ at point $P$ i.e.
$dB=\frac{\mu_{\circ}}{4 \pi} \frac{i \: dl\: sin\theta}{r^{2 }}$
Where $\theta$ is the angle between the length of the element $dl$ and the line joining the element to the point $P$. Here this angle is $90^{\circ}$
$dB=\frac{\mu_{\circ}}{4\pi} \frac{i \: dl}{r^{2}}\qquad(1)$
The direction of the magnetic field $d\overrightarrow{B}$ is in the plane of the paper and at right angles to the line $r$ as shown in the figure below (By applying the right-hand screw rule). It can be resolved into two components, one is vertical component of magnitude $dB\: sin\phi$ along the axis of the loop and the other is horizontal component of magnitude $dB\: cos\phi$ at right angles to the axis.
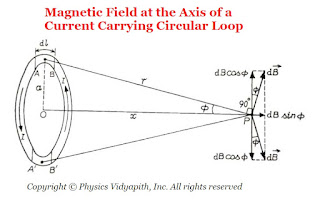 |
| Magnetic Field at the Axis of a Current-Carrying Circular Loop |
Let us consider another current element of the same length at the bottom of the loop, directly opposite to the first element, which is at right angles to the plane of the page but directed inwards. the field due to $d\overrightarrow{B}$ but directed as shown in the figure above. It is clear that components of both the fields at right angles to the axis are equal and opposite. Hence they cancel each other. The component along the axis are in the same direction and so they are added up.
If we imagine the whole of the loop to be divided into such current elements, the resultant field $\overrightarrow{B}$ at $P$ is directed along the axis and its magnitude is given by
$B=\int dB \: \sin\phi$
Now substitute the value of $dB$ from equation $(1)$
$B=\int \frac{\mu_{\circ}}{4\pi} \frac{i \: dl}{r^{2}} \: \sin\phi$
From figure, $sin\phi=\frac{a}{r}$, we get
$dB=\int \frac{\mu_{\circ}}{4 \pi} \frac{i}{r^{2}} \frac{a}{r}dl$
$dB=\int \frac{\mu_{\circ}}{4 \pi} \frac{ia}{r^{3}} dl$
$dB= \frac{\mu_{\circ}}{4 \pi} \frac{ia}{r^{3}} \int dl$
$dB= \frac{\mu_{\circ}}{4 \pi} \frac{ia}{r^{3}} 2 \pi \: a \qquad \left( \int dl = 2 \pi \: a \right)$
$dB= \frac{\mu_{\circ}ia^{2}}{2r^{3}}$
Agian from figure $r^{2}=\left( a^{2} + x^{2}\right)^{3}$ or $r= \left( a^{2} + x^{2}\right)^{3/2}$. Now substitute the value of $r$ in above equation.
$B=\frac{\mu_{\circ}\: i\: a^{2}}{2(a^{2}+x^{2})^{3/2}}$
If it is a coil of $N$ turns, then each turn will contribute equally to $B$. Thus
$B=\frac{\mu_{\circ}\: N \: i \: a^{2}}{2(a^{2}+x^{2})^{3/2}}$
The direction of the magnetic field $\overrightarrow{B}$ is along the axis of the loop and that of the coil.
Magnetic field at the Centre of the Loop→
At the centre of the coil, we have $x=0$
$B=\frac{\mu_{\circ}\: N \: i}{2a}$
Again the direction of the magnetic field $\overrightarrow{B}$ is perpendicular to the plane of the coil i.e. Along the axis of the coil.





