Paramagnetic Substances and Its properties
Paramagnetic Substances :
Those substances, which are placed in the external magnetic field and they are weakly magnetized in the direction of the external magnetic field, are called paramagnetic substances.
The susceptibility $\chi_{m} $ of paramagnetic substances is small and positive. Further, When a paramagnetic substance is placed in the magnetic field, then the flux density of the paramagnetic substance is slightly more than the free space. Thus, the relative permeability of paramagnetic substance $\mu_{r}$, is slightly more than 1.
Properties of Paramagnetic substances:
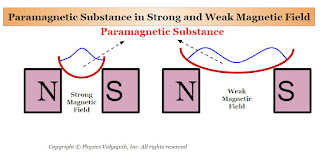
1. When a rod of a paramagnetic material is suspended freely between external magnetic poles (i.e. Between North and South Poles) then its axis becomes along the direction of the external magnetic field $B$ (Figure). The poles produced on the two sides of the rod are opposite to the poles of the external magnetic field.
2. In a non-uniform magnetic field, a paramagnetic substance tends to move from the weaker magnetic field to the stronger magnetic field. If a paramagnetic liquid is taken in a watch glass placed on two magnetic poles very near to each other, then the liquid rises in the middle as shown in the figure below(Figure) where the field is strongest. Now, if the distance between the poles is increased, the liquid is depressed in the middle, because now the field is strongest near the poles.
3. If the solution of a paramagnetic substance is poured into a U-tube and apply the strong magnetic field into one arm of this U-tube then the level of the solution in that arm rises. As shown in the figure below:
4. When paramagnetic gas molecules are passed between the poles of a magnet then paramagnetic gas molecules are attracted toward the magnetic field.
5. The susceptibility of a paramagnetic substance is inversely dependent on temperature.
$\chi \propto \frac{1}{T_{C}-T}$
Explanation of Paramagnetism on the Basis of Atomic Model:
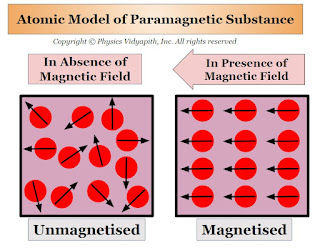
The property of Paramagnetism is generally found in those substances whose atoms (or ions or molecules) have an 'odd' number of electrons. In these odd numbers of electrons one electron is not able to form a pair because the net magnetic dipole moment of the atoms (or ions or molecules) are not zero. but in the absence of an external magnetic field, these magnetic dipole moments are randomly arranged inside the substance because the net magnetic dipole moment of the material is zero.
When a paramagnetic substance is placed in an external magnetic field $B$ then the magnetic dipole moment of the atoms (or ions or molecules) are weakly aligned in the direction of the external magnetic field. Thus, a small magnetic dipole moment is induced in the substance which is directly proportional to the magnetic field $B$. Hence, the paramagnetic substance is magnetized in the direction of the external magnetic field $B$, and the field lines become less dense inside the paramagnetic substance compared to those outside.