Conversion of Galvanometer into a Voltmeter

What is a voltmeter?

A voltmeter is an instrument used to measure potential differences between two points in an electric circuit directly in volts. The instrument measuring the potential difference of the order of millivolt $(mV)$ is called a millivoltmeter. An ideal voltmeter has infinite resistance.

Galvanometer used as voltmeter:

To use the galvanometer as a voltmeter in the circuit, The resistance of the galvanometer should be very high or almost infinite as compared to the other resistance of the circuit. Because the internal resistance of an ideal voltmeter is infinity.

So a high resistance is connected in series with the galvanometer (pivoted-type moving-coil galvanometer).

When a high resistance is connected in series to the galvanometer then the resultant resistance increases as compared to the other resistance of the circuit and it can be easily used as an ammeter and the actual potential difference can be measured through it.

Mathematical Analysis:

Let us consider, $G$ is the resistance of the coil of the Galvanometer, and the $i_{g}$ current, passing through it, produces full-scale deflection. If $V$ is the maximum potential difference that exists between two points $a$ and $b$ in the circuit. On connecting the galvanometer across the points $a$ and $b$, a current $i_{g}$ passes through the galvanometer and a high resistance $R$ is connected in series with galvanometer then

$i_{g}= \frac{V}{G + R}$

$G + R= \frac{V}{i_{g}}$

$R= \left(\frac{V}{i_{g}}\right ) - G$

If the current $i_{g}$ in the coil produces a full-scale deflection, then for the potential difference $V$ between the points $a$ and $b$, there will be a full scale deflection. Thus, on connecting a resistance $R$ of the above valve in series with the galvanometer, the galvanometer will become a voltmeter of range $0$ to $V$ Volt.

Note:

For the voltmeter, a high resistance is connected in series with the galvanometer and so the resistance of a voltmeter is very high compared to that of a galvanometer.

Resistance of voltmeter

$R_{v}=R+G$

Read More

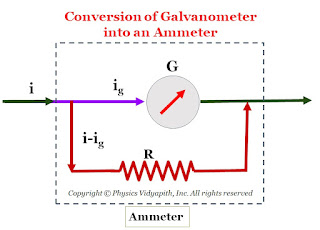
Conversion of Galvanometer into an Ammeter

What is Ammeter?

An Ammeter is an instrument that is used to measure the electric current in the electric circuits directly in Ampere. The instrument which measures the current of the order of milliampere $(mA)$ is called the milliammeter. The internal resistance of the ideal ammeter is always zero.

What is Galvanometer?

The galvanometer is an instrument that is used to measure the very small amount of the electric charge passing through the circuit. The internal resistance of the Galvanometer is not zero.

Galvanometer used as Ammeter: To use the galvanometer as an ammeter in the circuit, The resistance of the galvanometer should be very small or almost zero as compared to the other resistance of the circuit. Because the internal resistance of an ideal ammeter is zero.

So a low resistance is connected in parallel to the galvanometer which is known as a shunt.

When a low resistance is connected in parallel to the galvanometer then the resultant resistance decreases as compared to the other resistance of the circuit and it can be easily used as an ammeter and the actual current can be measured through it.

Mathematical Analysis:

Let us consider, $G$ is the resistance of the coil of the galvanometer and the $i_{g}$ current, passing through it, produces full scale deflection. If $i$ is the maximum current of the circuit then a part of current $i_{g}$ passes through the galvanometer and the remaining current $(i-i_{g})$ passes through the shunt $S$. Since $S$ and $G$ are parallel, the potential difference across them will be the same:

$i_{g} \times G = \left( i- i_{g} \right) \times S \qquad(1)$

$\frac{i_{g}}{i}=\frac{S}{S+G}$

i.e. only $\frac{S}{S+G}$th part of the total current will flow in the coil of the Galvanometer. Again from equation $(1)$:

$S=\left(\frac{i_{g}}{i-i_{g}}\right)G \qquad(2)$

If the current $i_{g}$ passes through the coil of the galvanometer and produces a full-scale deflection on the meter scale of a galvanometer, then the current $i$ in the circuit corresponds to the full-scale deflection. Thus, with a shunt $S$ of the above value, the galvanometer will be an ammeter in the range $0$ to $i$ ampere.

Example: Let a current of $1 A$ in the coil of a galvanometer produce a full-scale deflection. To convert it into an ammeter of range $10A$, a shunt is required such that when the current in the circuit is $10A$, only $1A$ flows in the coil remaining passes through the shunt. Now From substitute the $i_{g}=1A$ and $i=10A$ in the above equation $(2)$:

$\frac{S}{G}= \frac{1}{\left( 10 -1 \right)}$

$\frac{S}{G}= \frac{1}{9}$

The resistance of the shunt should be only $\frac{1}{9}$th the resistance of the galvanometer coil.

Note: As the shunt resistance value is very small so the combined resistance of the galvanometer and the shunt also becomes very small and hence the ammeter has a much smaller resistance than the galvanometer.

Resistance of Ammeter:

$\frac{1}{R_{A}}=\frac{1}{G}+\frac{1}{S}$

$R=\frac{G\:S}{G+S}$

When a Galvanometer is used in the circuit and connected in the series to measure the electric current:

The galvanometer is used in series to measure the electric current of the circuit so that the whole amount of the current passes through it. but the galvanometer will have some resistance due to the resultant resistance of the circuit increasing and the current in the circuit somewhat decreasing. Therefore the current read by the Galvanometer is less than the actual current.

Read More

Magnetic dipole moment of a revolving electron

The magnetic dipole moment of a revolving electron (Or Magnetic Moment due to Orbital Angular Momentum):

An electron revolving in an orbit about the nucleus of an atom behaves like a current carrying loop. It is called a minute current-loop and produces a magnetic field. Every current loop is associated with a magnetic moment.

Magnetic Dipole Moment of a Revolving Electron

Let us consider, that the magnetic moment associated with a loop carrying current $i$ and having area $A$ is:

$\mu_{L}= i.A \qquad(1)$

The current due to a revolving electron is

$i=\frac{e}{T}$

Where

$T$- The period of revolution of electron motion around the nucleus i.e $T=\frac{2 \pi r}{v}$
$e$- Charge on an electron So from the above equation

$i=\frac{e}{\frac{2 \pi r}{v}}$

$i=\frac{ev}{2 \pi r} \qquad(2)$

The area of the current loop is:

$A=\pi r^{2} \qquad(3)$

Now put the value of $i$ and $A$ in equation $(1)$

$\mu_{L}= \left( \frac{ev}{2 \pi r} \right) \left( \pi r^{2} \right)$

$\mu_{L}= \frac{evr}{2} \qquad(4)$

$\mu_{L}= \left(\frac{evr}{2}\right) \left( \frac{m}{m} \right)$

$\mu_{L}= \left(\frac{e}{2m}\right) \left( mvr \right)$

$\mu_{L}= \left(\frac{e}{2m}\right) L \qquad(5) \qquad (\because L=mvr) $

Where $L$- The orbital angular momentum of the electron and another value of $L$ is

$L=\frac{nh}{2\pi} \qquad(6)$

$\mu_{L}= \left(\frac{e}{2m}\right) \frac{nh}{2\pi}$

$\mu_{L}= n \: \left(\frac{eh}{4m \pi}\right)$

Where $n=1,2,3......$ is the principle quantum number.

This equation gives the magnetic moment associated with the orbital motion of the electron.

Bohr Magneton:

Bohr Magneton is defined as the angular momentum of an eletcron in ground state.

We know that:

Principle Quantum Number$(n)=1$

Charge of a electron $(e)=1.6\times10^{-19} C$

Planck Constant $(h)= 6.623 \times 10^{-34} J-sec$

Mass of electron $(m)= 9.1 \times 10^{-31} Kg$

So the magnetic moment of an electron in the ground state:

$\mu_{B}= n \: \left(\frac{eh}{4m \pi}\right)$

Now subtitute the value of $n,e,h,m$ in above equation:

$\mu_{B}= \frac{1 \times 1.6\times10^{-19} \times 6.623 \times 10^{-34} }{4 \times 3.14 \times 9.1 \times 10^{-31} }$

$\mu_{B}= 9.274 \times 10^{-24} A-m^{2}$

The magnetic moments due to orbital motion of electrons in higher orbits are multiples of the Bohr magneton value.

Read More

Magnetic potential energy of current-loop in a magnetic field

Magnetic potential energy:

When a current carrying loop is placed in an external magnetic field the torque is acted upon the current loop which tends to rotate the current loop in a magnetic field. Therefore the work is done to change the orientation of the current loop against the torque. This work is stored in the form of magnetic potential energy in the current loop. This is known as the magnetic potential energy of the current loop.

Note: The current loop has magnetic potential energy depending upon its orientation in the magnetic field.

Derivation of Potential energy of current-loop in a magnetic field:

Let us consider, A current loop of magnetic moment $\overrightarrow{m}$ is held with its axis at an angle $\theta$ with the direction of a uniform magnetic field $\overrightarrow{B}$. The magnitude of the torque acting on the current loop or magnetic dipole is

$\tau=m \: B \: sin\theta \qquad(1)$

Now, the current loop is rotated through an infinitesimally small angle $d\theta$ against the torque. The work done to rotate the current loop

$dW=\tau \: d\theta$

$dW=m \: B \: sin\theta \: d\theta $ {from equation $(1)$}

If the current loop is rotated from an angle (or orientation) $\theta_{1}$ to $\theta_{2}$ then the work done

$W=\int_{\theta_{1}}^{\theta_{2}} m \: B \: sin\theta d\theta$

$W= m \: B \: \left[ -cos\theta \right]_{\theta_{1}}^{\theta_{2}} $

$W= m \: B \: \left( cos\theta_{1} - cos\theta_{2} \right) $

This work is stored in the form of potential energy $U$ of the current loop :

$U= m \: B \: \left( cos\theta_{1} - cos\theta_{2} \right) $

If $\theta_{1}=90^{\circ}$ and $\theta_{2}= \theta$

$U= m \: B \: \left( cos90^{\circ} - cos\theta \right) $

$U= - m \: B \: cos\theta $

$U= - \overrightarrow{m} . \overrightarrow{B}$

Thus, a current loop has minimum potential energy when $\overrightarrow{m}$ and $\overrightarrow{B}$ are parallel and maximum potential energy when $\overrightarrow{m}$ and $\overrightarrow{B}$ are antiparallel.

Read More

Magnetic Dipole Moment of Current carrying loop

Current carrying Loop or Coil or Solenoid:

The current carrying loop (or Coil or solenoid) behaves like a bar magnet. A bar magnet with the north and south poles at its ends is a magnetic dipole, so a current -loop is also a magnetic dipole.

Equation of Magnetic Dipole Moment of Current carrying Loop:

When a current loop is suspended in a magnetic field, it experiences the torque which tends to rotate the current loop to a position in which the axis of the loop is parallel to the field. So the magnitude of the torque acting on the current loop in the uniform magnetic field $\overrightarrow{B}$ is given by:

$\tau=iAB sin\theta \qquad(1)$

Where $A$ - Area of the current loop

We also know that when the electric dipole is placed in the electric field, it also experiences the torque which tends to rotate the electric dipole in the electric field. So the magnitude of the torque on the electric dipole in the uniform electric field $\overrightarrow{E}$ is given by:

$\tau=pE sin\theta \qquad(2)$

Where $p$ - The magnitude of the electric dipole moment

Now compare the equation $(1)$ and equation $(2)$ and we can conclude that the current loop also has a magnetic dipole moment just like an electric dipole have an electric dipole moment. The magnetic dipole moment is associated with the current in the loop and the area of the current loop. It is represented by $\overrightarrow {m}$. So the magnitude of the magnetic dipole moment of current carrying loop is:

$m=iA$

The vector form of the magnetic dipole moment current carrying loop is

$\overrightarrow{m} = i\overrightarrow{A}$

The magnetic dipole moment of current carrying coil: If the current-carrying loop has $N$ number of turns (i.e current carrying coil) then the magnetic dipole moment of current carrying coil:

$m=NiA$

The vector form of the magnetic dipole moment of the current carrying coil is

$\overrightarrow{m} =N i\overrightarrow{A}$

The magnetic dipole moment of Circular Loop: Let us consider the circular loop of radius $a$ in which current $i$ is flowing the magnitude of the magnetic dipole moment of the circular loop:

$m=i A$

Here the area $A$ of the circular loop is $\pi a^{2}$ then the magnitude of the magnetic dipole moment of the circular loop is:

$m=i \pi a^{2} \qquad(3)$

The magnetic field at the center of the current carrying a circular loop in terms of current is:

$B=\frac{\mu_{\circ}i}{2a}$

Now substitute the value of $i$ from equation $(3)$ in the above equation then the magnetic field at the center of the current carrying circular loop in terms of magnetic dipole moment is:

$B=\frac{\mu_{\circ}m}{2\pi a^{3}}$

$B=\frac{\mu_{\circ}}{4\pi} \frac{2m}{a^{3}}$

Read More