Magnetic Field due to a Straight Current-Carrying Conductor of Finite Length

Derivation→

Let us consider, a current-carrying conductor $XY$ having length $l$ in which current $i$ is flowing from $X$ to $Y$. Now, To find the magnetic field due to the conductor, take a point $P$ at a distance $d$ from point $O$ of the conductor.

Now consider a small length element $dl$ at the conductor which is making an angle $\theta$ from point $P$. The length element $dl$ is also making the angle $d\theta$ from point $O$. If $\theta_{1}$ and $\theta_{2}$ is the angle from point $O$ to point $X$ and $Y$ respectively. Than magnetic field at point $P$ due to small length element $dl$ which is at a distance $r$

$dB=\frac{\mu_{0}}{4\pi} \frac{i\: dl \: sin (90+\theta)}{r^{2}}$

$dB=\frac{\mu_{0}}{4\pi} \frac{i \: dl \: cos\theta}{r^{2}} \qquad(1)$

Magnetic Field due to a Straight Current-Carrying Conductor of Finite Length

But from the figure, In $\Delta NOP$

$cos\theta=\frac{d}{r}$

$r=\frac{d}{cos\theta} \qquad(2)$

$tan\theta=\frac{l}{d}$

$l=d\:tan\theta$

Now differentiate the above equation with respect to $\theta$, then

$dl=d \: sec^{2}\theta \: d\theta \qquad(3)$

Now substitute the value of $dl$ and $r$ from equation$(2)$ and equation $(3)$ in equation$(1)$, then we get

$dB=\frac{\mu_{o}i}{4\pi}\frac{d \:sec^{2}\theta \: d\theta \: cos\theta}{\frac{d^{2}}{cos^{2}\theta}}$

$dB=\frac{\mu_{o}i}{4\pi}\frac{sec^{2}\theta \: d\theta \: cos^{3}\theta}{d}$

$dB=\frac{\mu_{o}i}{4\pi}\frac{cos\theta \: d\theta}{d} \qquad(4)$

The magnitude of the magnetic field $\overrightarrow{B}$ at point $P$ due to the whole conductor $XY$ is

$B=\int_{-\theta_{1}}^{\theta_{2}}dB$

Now substitute the value of $dB$ in above equation so

$B=\int_{-\theta_{1}}^{\theta_{2}} \frac{\mu_{o}i}{4\pi}\frac{cos\theta \: d\theta}{d} $

$B=\int_{-\theta_{1}}^{\theta_{2}} \frac{\mu_{o}i}{4\pi d}cos\theta d\theta $

$B= \frac{\mu_{o}i}{4\pi d} \left[ sin\theta\right] _{-\theta_{1}} ^{\theta_{2}} $

$B= \frac{\mu_{o}i}{4\pi d} \left[ sin(\theta _{2}) - sin(-\theta_{1})\right] $

$B=\frac{\mu_{o}i}{4\pi d}\left( sin\theta _{1} + sin\theta_{2}\right) $

Special Case→

1. For a conductor of infinite length, i.e $\theta_{1}=\theta_{2}=90^{\circ}$ then magnetic field
   
   
   $B=\frac{\mu_{0}}{4\pi} \frac{2i}{d} $
   
   

   $B=\frac{\mu_{0}}{2\pi} \frac{i}{d} $



2. If the point $P$ is at a distance $d$ near one end of the conductor,i.e. $\theta_{1}=90^{\circ}$ and $\theta_{2}=0$ then magnetic field
   
   

   $B=\frac{\mu_{0}}{4\pi} \frac{i}{d} $

   
   
   From the above equations, we can conclude that the magnetic field $B$ at point $P$ is proportional to the current $i$ and inversely proportional to the distance $d$ of point $P$ from the conductor.

The variation of the magnitude of magnetic field $B$ with distance $d$ is shown in the figure below→

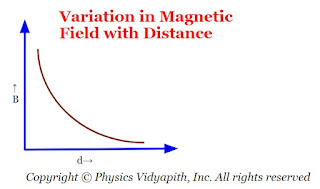Variation in Magnetic field with distance

The line of force of magnetic field $\overrightarrow{B}$ near a linear current-carrying conductor are concentric circles of varying radii with their centers at the conductor in a plane perpendicular to the conductor. The direction of the magnetic field $\overrightarrow{B}$ at a point $P$, distant $d$, will be along the tangent drawn on a circle of radius $d$ around the conductor.

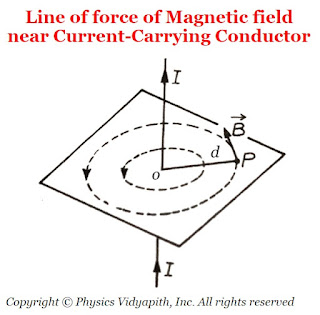Line of force of Magnetic field near Current-Carrying Conductor