What is Metre Bridge?
It is the simplest practical application of the Wheatstone's bridge that is used to measure an unknown resistance.
Principle: Its working is based on the principle of Wheatstone's Bridge.
When the Wheatstone's bridge is balanced
$\frac{P}{Q}=\frac{R}{S}$
Construction: It consists of usually one-meter long manganin wire of uniform cross-section, stretched along a meter scale fixed over a wooden board and with its two ends soldered to two L-shaped thick copper strips $A$ and $C$. Between these two copper strips, another copper strip is fixed so as to provide two gaps $mn$ and $m_{1}n_{1}$. A resistance box (R.B.) is connected in the gap $mn$ and the unknown resistance $S$ is connected in the gap $m_{1}n_{1}$. A cell of emf $E$, Key $(K)$, and rheostat are connected across $AC$. A movable jockey and a galvanometer are connected across the $BD$, as shown in the figure.
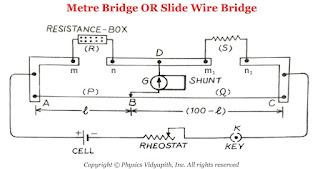 |
| Metre Bridge Or Slide Wire Bridge |
Working:
In a Metre bridge, First take out the suitable resistance $R$ from the resistance box after that move the jockey along the wire $AC$ till there is not any deflection in the galvanometer. This is the condition of a balanced Wheatstone's bridge. If $P$ and $Q$ are the resistance of the part $AB$ and $BC$ of the wire, then for the balanced condition of the bridge, we have,
$\frac{P}{Q}=\frac{R}{S} \qquad(1)$
Let us consider:
The total length of the wire $AC=100 \: cm$
Length of the part $AB$ of wire = $l \: cm$
Length of the part $BC$ of wire = $(100-l) \: cm$
Resistance per unit length of the wire = $\sigma$
Resistance of wire of uniform cross-section = $\infty$
$\frac{P}{Q}=\frac{Resistance \: of \: AB}{Resistance \: of \: BC}$
$\frac{P}{Q}=\frac{\sigma l }{\sigma \left( 100-l \right) }$
$\frac{P}{Q}=\frac{ l }{ \left( 100-l \right) } \qquad (2)$
Now substitute the value of equation $(2)$ in equation $(1)$ then we get
$\frac{R}{S}=\frac{ l }{ \left( 100-l \right) } $
$S=\frac{R(100-l)}{l}$
Where
$S$ → Unknown Resistance
$R$ →Standard Resistance





