Electric Potential due to an Electric Dipole:
The electric potential due to an electric dipole can be measured at different points:
- The electric potential on the axis of the electric dipole
- The electric potential on the equatorial line of the electric dipole
- The electric potential at any point of the electric dipole
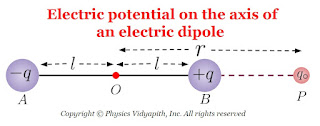
1. The electric potential on the axis of the electric dipole:
Let us consider, An electric dipole AB made up of two charges of -q and +q coulomb is placed in a vacuum or air at a very small distance of $2l$. Let a point $P$ is on the axis of an electric dipole and place at a distance $r$ from the center point $O$ of the electric dipole. Now put the test charged particle $q_{0}$ at point $P$ for the measurement of electric potential due to dipole's charges.
So Electric potential at point $P$ due $+q$ charge of electric dipole→
$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{r-l}$
The electric potential at point $P$ due $-q$ charge of electric dipole→
$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{r+l}$
Electric potential is a scalar quantity. Hence the resultant potential $V$ at the point $P$ will be the algebraic sum of the potential $V_{+q}$ and $V_{-q}$. i.e. →
$ V=V_{+q}+V_{-q}$
Now substitute the value of $V_{+q}$ and $V_{-q}$ in the above equation →
$ V= \frac{1}{4\pi \epsilon_{0}} \frac{q}{r-l} -\frac{1}{4\pi \epsilon_{0}} \frac{q}{r+l}$
$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{q}{r-l} - \frac{q}{r+l} \right]$
$ V= \frac{q}{4\pi \epsilon_{0}} \left[ \frac{1}{r-l} - \frac{1}{r+l} \right]$
$ V= \frac{q}{4\pi \epsilon_{0}} \left[ \frac{ \left( r+l \right)-\left (r-l \right)}{r^{2}-l^{2}} \right]$
$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{2ql}{r^{2}-l^{2}} \right]$
$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{p}{r^{2}-l^{2}} \right] \qquad \left( \because p=2ql\right)$
If $r$ is much larger then $2l$. So $l^{2}$ can be neglected in comparison to $r^{2}$. Therefore electric potential at the point $P$ due to the electric dipole is →
$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{p}{r^{2}} \right] $
2. The electric potential on the equatorial line of the electric dipole:
Let us consider, An electric dipole AB made up of two charges of $+q$ and $-q$ coulomb are placed in vacuum or air at a very small distance of $2l$. Let a point $P$ be on the equatorial line of an electric dipole and place it at a distance $r$ from the center point $O$ of the electric dipole. Now put the test charged particle $q_{0}$ at point $P$ for the measurement of electric potential due to dipole's charges.
So Electric potential at point $P$ due $+q$ charge of electric dipole→
$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{BP}$
$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}}$
The electric potential at point $P$ due $-q$ charge of electric dipole→
$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{AP}$
$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}}$
$\therefore$ The resultant potential at point $P$ is
$ V=V_{+q}+V_{-q}$
$ V=\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}}-\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}} $
$V=0 $
Thus, the electric potential is zero on the equatorial line of a dipole (but the intensity is not zero). So No work is done in moving a charge along this line.
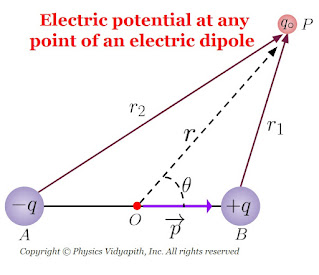
3. The electric potential at any point of the electric dipole:
Let us consider, an electric dipole $AB$ of length $2l$ consisting of the charge $+q$ and $-q$. Let's take a point $P$ in general and its distance is $r$ from the center point $O$ of the electric dipole AB.
Let the distance of point $P$ from the point $A$ and Point $B$ of the dipole is $PB=r_{1}$ and $PA=r_{2}$ respectively.
So, The electric potential at point $P$ due to the $+q$ charge of the electric dipole is →
$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{1}}$
$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{2}}$
The resultant potential at point $P$ is the algebraic sum of potential due to charges $+q$ and $-q$ of the dipole. That is
$ V=V_{+q}+V_{-q}$
$ V=\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{1}}-\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{2}}$
$ V=\frac{1}{4\pi \epsilon_{0}} \left(\frac{q}{r_{1}}-\frac{q}{r_{2}} \right) \qquad(1)$
Now simplify the above equation by applying the Geometry from the figure. i.e. From the figure, Acute angle $\angle POB$, we can write as,
$ r^{2}_{1}=r^{2}+l^{2}-2rlcos\theta \qquad(2)$
$ r^{2}_{2}=r^{2}+l^{2}-2rlcos \left(\pi - \theta \right)$
$ r^{2}_{2}=r^{2}+l^{2}+2rlcos \theta \qquad(3)$
The equation $(2)$ may be expressed as →
$ r^{2}_{1}=r^{2} \left[1+ \frac{l^{2}}{r^{2}}-\frac{2l}{r}cos\theta \right] $
Taking distance $r$ much greater than the length of dipole (i.e. r>>l), so we may retain only first order term in $\frac{l}{r}$,
$ \therefore r^{2}_{1}=r^{2} \left[1- \frac{2l}{r}cos\theta \right]$
$ r_{1}=r \left[1- \frac{2l}{r}cos\theta \right]^{\frac{1}{2}}$
$ \frac {1}{r_{1}}=\frac{1}{r} \left[1- \frac{2l}{r}cos\theta \right]^{-\frac{1}{2}}$
Now applying the binomial theorem in the above equation. So we get
$ \frac {1}{r_{1}}=\frac{1}{r} \left[1+ \frac{l}{r}cos\theta \right]$
Similarly,
$ \frac {1}{r_{2}}=\frac{1}{r} \left[1- \frac{l}{r}cos\theta \right]$
Substituting these values in equation $(1)$, we get
$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{q}{r} \left(1+ \frac{l}{r}cos\theta \right)-\frac{q}{r} \left(1- \frac{l}{r}cos\theta \right) \right]$
$ V=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r} \left[ \left(1+ \frac{l}{r}cos\theta \right)- \left(1- \frac{l}{r}cos\theta \right) \right]$
$ V=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r} \left[ \left(1+ \frac{l}{r}cos\theta \right)- \left(1- \frac{l}{r}cos\theta \right) \right]$
$ V=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r} \left[ \frac{2l cos\theta}{r}\right]$
$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{2ql cos\theta}{r^{2}}\right]$
But $q\times 2l=p$ (dipole moment)
$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{p cos\theta}{r^{2}}\right]$
The vector form of the above equation can be written as →
$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{\overrightarrow{p} \cdot \overrightarrow{r} }{r^{2}}\right]$
The above two equations hold only under the approximation that the distance of observation point $P$ is much greater than the size of the dipole.
Special Case:
- At axial points $\theta=0^{\circ}$,
then $cos\theta= cos 0^{\circ}=1$,
Therefore, $ V=\frac{1}{4\pi\epsilon_{0}} \frac{p}{r^{2}}$
- At equatorial points $\theta=90^{\circ}$,
then $cos\theta= cos 90^{\circ}=0$,
Therefore,$ \quad V=0$
Now comparing this result with the potential due to a point-charge, we see that:
- In a fixed direction, that is , fixed $\theta$, $V\propto \frac{1}{r^{2}}$. here rather than $V \propto \frac{1}{r}$;
- Even for a fixed distance $r$, there is now a dependence on direction, that is, on $\theta$.