Kepler's Laws of Planetary Motion

Kepler's Laws →

Kepler's found important uniformity in the motion of the planets. This uniformity is known as "Kepler's Laws of planetary motion". There are basically three laws →

First law (Law of orbits)

Second Law (Law of Areal Speed)

Third Law (Law of Periods)

First law (Law of orbits) →

All the planets move around the sun in elliptical path and the sun is at the one foci of the ellipse.

Second Law (Law of Areal Speed) →

A line joining the any planet to sun sweeps out equal areas in equal interval of of times. i.e The areal speed of the planets remains constant.

According to the second law, When the planet is farthest from the sun, then its speed is maximum, and when it is nearest the sun, then its speed is maximum.

Planetary Motion

From the above figure, A planet is moving around the sun from $A$ to $B$ in a given time interval, and from $C$ to $D$ in the same time interval, then according to the law of areal speed, the areas $ASB$ and $CSD$ will be equal with respect to the same time-interval

Proof →

Let us consider, A planet moves the angle $d\theta$ from $A$ to $B$ in the infinitesimal interval of time $dt$, then the area swept out by radial line $SA$ is

$dA$= Area of the curved $\Delta$ $SAB$

$dA \approx \frac{1}{2} \left( AB \times SA \right)$

$dA \approx \frac{1}{2} \left( r \: d\theta \times r \right)$

$dA \approx \frac{1}{2} \left( r^{2} \: d\theta \right)$

Thus, the instantaneous areal speed of the planets is

$\frac{dA}{dt}=\frac{1}{2} r^{2} \frac{d \theta}{dt}$

$\frac{dA}{dt}=\frac{1}{2} r^{2} \omega \qquad(1)$

Where $\omega$ → The angular speed of the planet.

We know that

$J=I \: \omega$

Where $I$ is the instantaneous moment of inertia of the planet about the Sun $S$.

$J=m \: r^{2} \: \omega \qquad(2)$

Where $m$ is the mass of the planet. Now substitute the value of $r^{2} \: \omega$ from equation $(2)$ in equation $(1)$.

$\frac{dA}{dt}=\frac{J}{2m} \left( Constant \right)$

From the above equation, The areal speed $\frac{dA}{dt}$ of the planet is constant which is Kepler's Second Law. The above equation shows that the angular momentum of the planet is constant. i.e. The angular momentum of any planet is conserved.

Third Law (Law of Periods) →

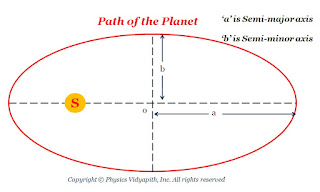
The square of the time period of one complete revolution of any planet around the sun is directly proportional to the cube of the semi-major axis of its elliptical orbit.

Path of the Planet

Proof →

Let $a$ and $b$ be the semi-major and semi-minor axes of the ellipse, then the area of the ellipse will be $\pi ab$. Let $T$ is the period of one complete revolution of any planet, then

$T=\frac{Area \: of \: the \: ellipse}{Areal \: Speed}$

$T=\frac{\pi a b}{\frac{J}{2m}}$

$T=\frac{2\pi a b m}{J}$

$T^{2}=\frac{4 \pi^{2} a^{2} b^{2} m^{2}}{J^{2}}$

Let $l$ be the semi-latus rectum of the elliptical orbit i.e. $l=\frac{b^{2}}{a}$. Then we get the above equation which can be written as

$T^{2}=\frac{4 \pi^{2} m^{2} a^{3} l }{J^{2}}$

$T^{2} \propto a^{3} $

Where $\frac{4 \pi^{2} m^{2} l }{J^{2}}$ is constant.

From the above equation, It is clear that the larger the distance of a planet from the sun, the larger will be its period of revolution around the sun. The period of revolution of the nearest planet to the sun i.e. Mercury is $88$ days, while that of the faraway planet from the sun i.e. Pluto is $248$ years.

Numerical Aperture and Acceptance Angle of the Optical Fibre

Angle of Acceptance → If incident angle of light on the core for which the incident angle on the core-cladding interface equals the critical angle then incident angle of light on the core is called the "Angle of Acceptance. Transmission of light when the incident angle is equal to the acceptance angle If the incident angle is greater than the acceptance angle i.e. $\theta_{i}>\theta_{0}$ then the angle of incidence on the core-cladding interface will be less than the critical angle due to which part of the incident light is transmitted into cladding as shown in the figure below Transmission of light when the incident angle is greater than the acceptance angle If the incident angle is less than the acceptance angle i.e. $\theta_{i}<\theta_{0}$ then the angle of incidence on the core-cladding interface will be greater than the critical angle for which total internal reflection takes place inside the core. As shown in the figure below Transmission of lig

click here »

Fraunhofer diffraction due to a single slit

Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is incident normally from $S$ on a narrow slit $AB$ of width $e$ and is diffracted from it. The diffracted beam is focused at the screen $XY$ by another converging lens $L_{2}$. The diffraction pattern having a central bright band followed by an alternative dark and bright band of decreasing intensity on both sides is obtained. Analytical Explanation: The light from the source $S$ is incident as a plane wavefront on the slit $AB$. According to Huygens's wave theory, every point in $AB$ sends out secondary waves in all directions. The undeviated ray from $AB$ is focused at $C$ on the screen by the lens $L_{2}$ while the rays diffracted through an angle $\theta$ are focussed at point $p$ on the screen. The rays from the ends $A$ and $B$ reach $C$ in the same phase and hence the intensity is maximum. Fraunhofer diffraction due to

click here »

Particle in one dimensional box (Infinite Potential Well)

Let us consider a particle of mass $m$ that is confined to one-dimensional region $0 \leq x \leq L$ or the particle is restricted to move along the $x$-axis between $x=0$ and $x=L$. Let the particle can move freely in either direction, between $x=0$ and $x=L$. The endpoints of the region behave as ideally reflecting barriers so that the particle can not leave the region. A potential energy function $V(x)$ for this situation is shown in the figure below. Particle in One-Dimensional Box(Infinite Potential Well) The potential energy inside the one -dimensional box can be represented as $\begin{Bmatrix} V(x)=0 &for \: 0\leq x \leq L \\ V(x)=\infty & for \: 0> x > L \\ \end{Bmatrix}$ $\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2m}{\hbar^{2}}(E-V)\psi(x)=0 \qquad(1)$ If the particle is free in a one-dimensional box, Schrodinger's wave equation can be written as: $\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2mE}{\hbar^{2}}\psi(x)=0$ $\frac{d^{2} \psi(x)}{d x

click here »

Physics Vidyapith ✍️

Search This Blog