Self Induction Phenomenon and its Coefficient

Self Induction:

When a changing current flows in a coil then due to the change in magnetic flux in the coil produces an electro-motive force $\left(emf \right)$ in that coil. This phenomenon is called the principle of Self Induction.

The direction of electro-motive force can be found by applying "Lenz's Law".

Mathematical Analysis of Coefficient of Self Induction:

Let us consider that a coil having the number of turns is $N$. If the change in current is $i$, then linkage flux in a coil will be

$N \phi \propto i$

$N\phi = L i \qquad(1)$

Where $L$ $\rightarrow$ Coefficient of Self Induction.

According to Faraday's law of electromagnetic induction. The electro-motive force $\left(emf \right)$ in a coil is

$e=-N\left( \frac{d \phi}{dt} \right)$

$e=-\frac{d \left(N \phi \right)}{dt} \qquad(2)$

From equation $(1)$ and equation $(2)$

$e=-\frac{d \left(L i\right)}{dt} $

$e=-L \left(\frac{d i}{dt} \right) $

$L = \frac{e}{\left(\frac{d i}{dt} \right)}$

If $\left(\frac{d i}{dt} \right) = 1$

Then

$L = e$

The above equation shows that If the rate of flow of current in a coil is unit then the coefficient of self-induction in that coil will be equal to the induced electro-motive force $\left( emf \right)$.

Read More

Mutual Induction Phenomenon and its Coefficient

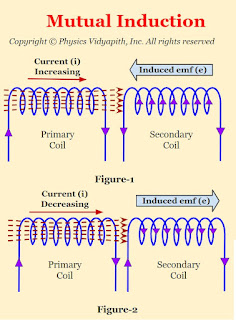
Mutual Induction:

When two coils are placed near each other then the change in current in one coil ( Primary Coil) produces electro-motive force $\left( emf \right)$ in the adjacent coil ( i.e. secondary coil). This phenomenon is called the principle of Mutual Induction.

The direction of electro-motive force $\left( emf \right)$ depends or can be found by "Lenz's Law"

Mathematical Analysis of Coefficient of Mutual Induction:

Let us consider that two coils having the number of turns are $N_{1}$ and $N_{2}$. If these coils are placed near to each other and the change in current of the primary coil is $i_{1}$, then linkage flux in the secondary coil will be

$N_{2}\phi_{2} \propto i_{1}$

$N_{2}\phi_{2} = M i_{1} \qquad(1)$

Where $M$ $\rightarrow$ Coefficient of Mutual Induction.

According to Faraday's law of electromagnetic induction. The electro-motive force $\left( emf \right)$ in the secondary coil is

$e_{2}=-N_{2}\left( \frac{d \phi_{2}}{dt} \right)$

$e_{2}=-\frac{d \left(N_{2} \phi_{2} \right)}{dt} \qquad(2)$

From equation $(1)$ and equation $(2)$

$e_{2}=-\frac{d \left(M i_{1} \right)}{dt} $

$e_{2}=-M \left(\frac{d i_{1}}{dt} \right) $

$M = \frac{e_{2}}{\left(\frac{d i_{1}}{dt} \right)}$

If $\left(\frac{d i_{1}}{dt} \right) = 1$

Then

$M = e_{2}$

The above equation shows that If the rate of flow of current in the primary coil is unit then the coefficient of mutual induction will be equal to the induced electro-motive force $\left( emf \right)$ in the secondary coil.

Read More

Faraday's laws of electromagnetic induction

Faraday's Laws of Electromagnetic Induction:

The Faraday's experiment shows the two laws which are known as Farday's laws of electromagnetic induction

First Law (Neumann's Law): The rate of change of magnetic flux through a circuit is equal to the emf produced in the circuit. This is also known as "Neumann Law"

$e=-\frac{\Delta \phi}{ \Delta t}$

Here negative sign shows the direction of emf.

If $\Delta t \rightarrow 0$

$e=-\frac{d \phi}{ d t}$

This equation represents an independent experimental law that cannot be derived from other experimental laws.

If the circuit is a tightly wound coil of $N$ turns, then the induced emf

$e=-N\frac{d \phi}{ d t}$

$e=-\frac{d \left(N \phi\right)}{ dt}$

Here $N \phi$ is called the 'Linkage magnetic flux'.

Note: The change in flux induces emf, not the current.

Second Law (Lenz's Law): The direction of induced EMF produced in a closed circuit is such that it opposes the original cause that produces it. It is also called "Lenz's law". The direction of induced EMF is described by Fleming's right-hand rule.

Read More