Skip to main content

Force between two long and parallel current-carrying conductor

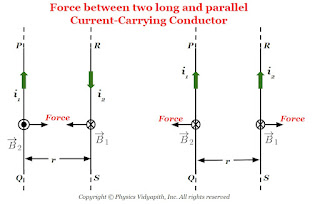
Derivation of Force between two long and parallel current-carrying conductors:

Let us consider:
  • The two long straight, parallel conductors = $PQ$ and $RS$

  • The length of the conductor= $l$

  • The distance between the parallel conductor = $r$

  • The current flowing in conductor $PQ$ = $i_{1}$

  • The current flowing in conductor $RS$ = $i_{2}$

  • The magnetic field due to conductor $PQ$ = $B_{1}$

  • The magnetic field due to conductor $RS$ = $B_{2}$

  • The magnetic force on conductor $PQ$= $F_{1}$

  • The magnetic force on conductor $RS$= $F_{2}$

    • The magnetic force between two long and parallel Current-Carrying Conductor
    Force Between Parallel Current Carrying Conductor
    Now Consider the magnetic force on conductor $RS$ is i.e.

    $F_{2}=i_{2}B_{1}l sin\theta$

    Where $\theta$ is the angle between the magnetic field and length element of conductor i.e. $\theta=90^{\circ}$ so above equation can be written as,

    $F_{2}=i_{2}B_{1}l sin 90^{\circ}$

    $F_{2}=i_{2}B_{1}l \qquad(1)$

    The magnetic field due to conductor PQ is:

    $B_{1}= \frac{\mu_{\circ}}{2\pi} \frac{i_{1}}{r}$

    Now substitute the value of $B_{1}$ in equation $(1)$ so the force on conductor $RS$

    $F_{2}=\frac{\mu_{\circ}}{2\pi} \frac{i_{1}i_{2}}{r}l $

    So the force per unit length on the conductor $RS$ is

    $\frac{F_{2}}{l}=\frac{\mu_{\circ}}{2\pi} \frac{i_{1}i_{2}}{r} \qquad(2)$

    Similarly, we can solve the force per unit length on the conductor $PQ$

    $\frac{F_{1}}{l}=\frac{\mu_{\circ}}{2\pi} \frac{i_{1}i_{2}}{r} \qquad(3)$

    So from the above equation, we can conclude that the force per unit length is the same on both conductors whether both have different amounts of current flowing. The generalized form of the force per unit length from the above equations is


    $\frac{F}{l}=\frac{\mu_{\circ}}{2\pi} \frac{i_{1}i_{2}}{r}$

    Note: When both parallel conductors have the same direction of current then the force between the conductor will be repulsive. or when both parallel conductors have opposite directions of current then the force between the conductor is attractive.
    Labels:

    Comments

    Post a Comment

    If you have any doubt. Please let me know.

    Popular Posts

    Numerical Aperture and Acceptance Angle of the Optical Fibre

    Angle of Acceptance → If incident angle of light on the core for which the incident angle on the core-cladding interface equals the critical angle then incident angle of light on the core is called the "Angle of Acceptance. Transmission of light when the incident angle is equal to the acceptance angle If the incident angle is greater than the acceptance angle i.e. $\theta_{i}>\theta_{0}$ then the angle of incidence on the core-cladding interface will be less than the critical angle due to which part of the incident light is transmitted into cladding as shown in the figure below Transmission of light when the incident angle is greater than the acceptance angle If the incident angle is less than the acceptance angle i.e. $\theta_{i}<\theta_{0}$ then the angle of incidence on the core-cladding interface will be greater than the critical angle for which total internal reflection takes place inside the core. As shown in the figure below Transmission of lig
    Post a Comment
    click here »

    Fraunhofer diffraction due to a single slit

    Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is incident normally from $S$ on a narrow slit $AB$ of width $e$ and is diffracted from it. The diffracted beam is focused at the screen $XY$ by another converging lens $L_{2}$. The diffraction pattern having a central bright band followed by an alternative dark and bright band of decreasing intensity on both sides is obtained. Analytical Explanation: The light from the source $S$ is incident as a plane wavefront on the slit $AB$. According to Huygens's wave theory, every point in $AB$ sends out secondary waves in all directions. The undeviated ray from $AB$ is focused at $C$ on the screen by the lens $L_{2}$ while the rays diffracted through an angle $\theta$ are focussed at point $p$ on the screen. The rays from the ends $A$ and $B$ reach $C$ in the same phase and hence the intensity is maximum. Fraunhofer diffraction due to
    Post a Comment
    click here »

    Particle in one dimensional box (Infinite Potential Well)

    Let us consider a particle of mass $m$ that is confined to one-dimensional region $0 \leq x \leq L$ or the particle is restricted to move along the $x$-axis between $x=0$ and $x=L$. Let the particle can move freely in either direction, between $x=0$ and $x=L$. The endpoints of the region behave as ideally reflecting barriers so that the particle can not leave the region. A potential energy function $V(x)$ for this situation is shown in the figure below. Particle in One-Dimensional Box(Infinite Potential Well) The potential energy inside the one -dimensional box can be represented as $\begin{Bmatrix} V(x)=0 &for \: 0\leq x \leq L \\ V(x)=\infty & for \: 0> x > L \\ \end{Bmatrix}$ $\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2m}{\hbar^{2}}(E-V)\psi(x)=0 \qquad(1)$ If the particle is free in a one-dimensional box, Schrodinger's wave equation can be written as: $\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2mE}{\hbar^{2}}\psi(x)=0$ $\frac{d^{2} \psi(x)}{d x
    Post a Comment
    click here »