Principle, Construction and Working of Current Carrying Solenoid

Current Carrying Solenoid:

The Solenoid is an artificial magnet which is used for different purposes.

Principle of Solenoid:

The principle of the solenoid is based on the "Ampere Circuital Law" and its magnetic field is raised due to the current carrying a circular loop.

Construction of Solenoid:

The current carrying solenoid is consist of insulated cylindrical material and conducting wire. The conducting wire like copper is wrapped closely around the insulated cylindrical material ( like cardboard, clay, or plastic). The end faces of the conducting wire are connected to the battery.

Long Current Carrying Solenoid

Working:

When the electric current flow in the solenoid then a field (i.e. Magnetic field) is produced around and within the current carrying solenoid. This magnetic field is produced in solenoid due to circular loops of the solenoid and the direction of the magnetic field is depend upon the direction of the electric current flow in the circular loop. The magnetic field within the current carrying solenoid is uniform and parallel to the axis of the solenoid.

Derivation of the magnetic field due to long current carrying Solenoid:

Cross Section View of Long Current Carrying Solenoid

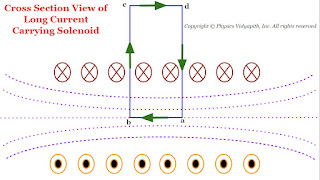Cross Section View of the long Current Carrying Solenoid

Let us consider a very long current carrying solenoid of length $l$ in which $i$ electric current is flowing. Here its diameter is very less as compared to the length of the solenoid.

Now take a closed rectangular path $abcd$ in which the side $ab$ is parallel to the axis of the solenoid and sides $bc$ and $da$ are very long so that the side $cd$ is far from the solenoid and the magnetic field at this side is negligibly small.

Now apply Ampere's circuital law to the rectangular path $abcd$

$\oint \overrightarrow{B}. \overrightarrow{dl}=\mu_{\circ} i' \qquad(1)$

Where $i'$ is the current enclosed by the rectangle.

Let $n$ is the number of turns per unit length of the solenoid. So the number of turns in a length $x$ is = $nx$

The current in each turn is $i$ then the net current $(i')$ enclosed by the rectangle $abcd$ is $nxi$ i.e

$i'=nxi$

Now substitute the value of $i'$ in above equation $(1)$

$\oint \overrightarrow{B}. \overrightarrow{dl}=\mu_{\circ} nxi \qquad(2)$

Now expand the Ampere circuital law for closed rectangular $abcd$-

$\oint \overrightarrow{B}.\overrightarrow{dl}=\int_{a}^{b} \overrightarrow{B}.\overrightarrow{dl}+ \int_{b}^{c} \overrightarrow{B}.\overrightarrow{dl} + \int_{c}^{d} \overrightarrow{B}.\overrightarrow{dl} + \int_{d}^{a} \overrightarrow{B}.\overrightarrow{dl} \qquad(3)$

In above equation the term:

$\int_{b}^{c} \overrightarrow{B}.\overrightarrow{dl}= \int_{d}^{a} \overrightarrow{B}.\overrightarrow{dl}=0$

The above term is zero because along $bc$ and $da$ the magnetic field $\overrightarrow{B}$ and length element $\overrightarrow{dl}$ are perpendicular to each other.

$\int_{c}^{d} \overrightarrow{B}.\overrightarrow{dl}=0 $

The above term is zero because the magnetic field $\overrightarrow{B}$ outside the solenoid is negligible due long length of the solenoid.

The above equation $(3)$ can be written by applying the above condition-

$\oint \overrightarrow{B}.\overrightarrow{dl}=\int_{a}^{b} \overrightarrow{B}.\overrightarrow{dl}$

$\oint \overrightarrow{B}.\overrightarrow{dl}= \overrightarrow{B}\int_{a}^{b} \overrightarrow{dl}$

$\oint \overrightarrow{B}.\overrightarrow{dl}= B x \qquad(4)$

Where $x$- Length of $ab$

From equation $(2)$ and equation $(4)$, we get

$Bx=\mu_{\circ}nxl$

$B=\mu_{\circ}nl$

Numerical Aperture and Acceptance Angle of the Optical Fibre

Angle of Acceptance → If incident angle of light on the core for which the incident angle on the core-cladding interface equals the critical angle then incident angle of light on the core is called the "Angle of Acceptance. Transmission of light when the incident angle is equal to the acceptance angle If the incident angle is greater than the acceptance angle i.e. $\theta_{i}>\theta_{0}$ then the angle of incidence on the core-cladding interface will be less than the critical angle due to which part of the incident light is transmitted into cladding as shown in the figure below Transmission of light when the incident angle is greater than the acceptance angle If the incident angle is less than the acceptance angle i.e. $\theta_{i}<\theta_{0}$ then the angle of incidence on the core-cladding interface will be greater than the critical angle for which total internal reflection takes place inside the core. As shown in the figure below Transmission of lig

click here »

Fraunhofer diffraction due to a single slit

Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is incident normally from $S$ on a narrow slit $AB$ of width $e$ and is diffracted from it. The diffracted beam is focused at the screen $XY$ by another converging lens $L_{2}$. The diffraction pattern having a central bright band followed by an alternative dark and bright band of decreasing intensity on both sides is obtained. Analytical Explanation: The light from the source $S$ is incident as a plane wavefront on the slit $AB$. According to Huygens's wave theory, every point in $AB$ sends out secondary waves in all directions. The undeviated ray from $AB$ is focused at $C$ on the screen by the lens $L_{2}$ while the rays diffracted through an angle $\theta$ are focussed at point $p$ on the screen. The rays from the ends $A$ and $B$ reach $C$ in the same phase and hence the intensity is maximum. Fraunhofer diffraction due to

click here »

Particle in one dimensional box (Infinite Potential Well)

Let us consider a particle of mass $m$ that is confined to one-dimensional region $0 \leq x \leq L$ or the particle is restricted to move along the $x$-axis between $x=0$ and $x=L$. Let the particle can move freely in either direction, between $x=0$ and $x=L$. The endpoints of the region behave as ideally reflecting barriers so that the particle can not leave the region. A potential energy function $V(x)$ for this situation is shown in the figure below. Particle in One-Dimensional Box(Infinite Potential Well) The potential energy inside the one -dimensional box can be represented as $\begin{Bmatrix} V(x)=0 &for \: 0\leq x \leq L \\ V(x)=\infty & for \: 0> x > L \\ \end{Bmatrix}$ $\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2m}{\hbar^{2}}(E-V)\psi(x)=0 \qquad(1)$ If the particle is free in a one-dimensional box, Schrodinger's wave equation can be written as: $\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2mE}{\hbar^{2}}\psi(x)=0$ $\frac{d^{2} \psi(x)}{d x

click here »

Physics Vidyapith ✍️

Search This Blog