Electric Field:
That region around any charged particle (source-charge) in which other test charged particle experience an electric force (attraction or repulsion). This region is called electric field of that charged particle.
The size and magnitude of the test charged particle is very small i.e tends to zero which does not modify the electric field of source charged particle. The electric field can only experience, not be seen by eyes. The electric field is defined by imaginary lines which are called
electric field lines.
Electric Field Lines:
Electric field lines are imaginary lines that describe the behavior of electric fields. The behavior of the electric field tells about the force acting on free test-charged particles. This force gives the motion to the free test charge particle which is placed in the path of the electric field line. So the test charged particle moves in the direction of the electric field line. Hence, the direction of electric force and electric field lines both are the same. Thus electric field line is also known as
electric lines of force.
Electric Lines of Force:
An electric line of force is defined as an imaginary smooth curve drawn in electric field along which a free isolated test charged particle moves. The tangent drawn at any point on the electric line of force gives the direction of the force acting on a test charged particle placed at that point.
Properties of Electric Line of Force:
There are the following properties of the electric line of force:
1.) The direction of the electric line of force is outward for positively charged particles, and inward for negatively charged particles.
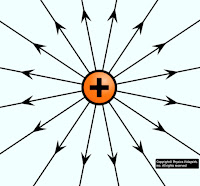 |
| Electric field line of positive charge |
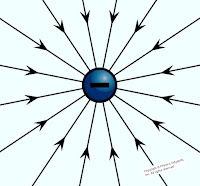 |
| Electric field line of negative charge |
So when two opposite charge are placed near each other, the electric line of force start from a positive charge and end at a negative charge
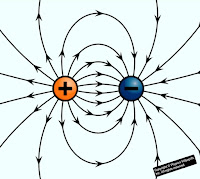 |
| Electric lines of force of unlike charges |
When two same nature charges are placed near each other, the field produced by one charge is equal and opposite to the field produced by the other charges at the midpoint of the line joining the two charges. Therefore, at this point, the resultant electric field is zero. This point is called the
neutral point.
 |
| Electric lines of force of like charges |
2.) The tangent drawn at any point on the line of force gives the direction of the force acting on a test-charged particle at that point.
3.) Two electric lines of force can never intersect with each other because if they do so then at the point of intersection two tangents can be drawn which would mean that there are two directions of the force at that point which is impossible.
4.) When electric lines of force are closer to each other, the electric field is stronger in this region. And where The line of force are far away from each other then the electric field is weaker in this region. When the line of force are parallel and in a straight line to each other, the electric field is known as the
uniform electric field.
5.) The electric line of force has a tendency to contract in length like a stretched elastic string for the opposite nature of the charged particle. It is due to the attraction force between charged particles.
6.) The electric line of force has a tendency to separate from each other in the direction perpendicular to their length for the same nature of charged particles. It is due to the repulsion force between charged particles.
7.) The electric lines of force can never form closed loops as a line can never start and end on the same charge.
8.) The electric line of force also gives us an indication of the equipotential surface (That surface which has the same potential on each point of the surface).
9.) The electric line of force always flows from higher potential to lower potential.
10.) In a region where there is no electric field, lines are absent so the electric field inside the conductor is zero. Electric lines of force end or start normally from the surface of a conductor.








