Force on current carrying conductor in uniform magnetic field

Derivation of force on current-carrying conductor in uniform magnetic field:

Let us consider:

The length of the conductor - $l$

The cross-section area of the current carrying conductor - $A$

The current flow in a conductor- $i$

The drift or average velocity of the free electrons - $v_{d}$

The current-carrying conductor is placed in a magnetic field - $B$

The total number of free electrons in the current carrying conductor - $N$

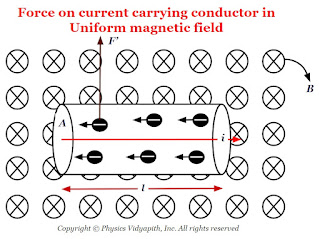Force on current carrying conductor in the uniform magnetic field

Now the magnetic force on one free electron in a conductor -

$F'= ev_{d}B sin\theta \qquad(1)$

The net force on the conductor is due to all the free electrons present in the conductor

$F=N\: F' \qquad(2)$

Let $N$ is the number of free electrons per unit volume of conductor. So the total number of free electrons in the $Al$ volume of the conductor will be

$N=nAl \qquad(3)$

Now substitute the value of $N$ and $F'$ from above equation $(1)$ and equation $(3)$ in equation $(2)$

$F=neAlv_{d}B\: sin\theta$

Where $i=neAv_{d}$

So from the above equation

$F=ilB \: sin\theta $

The Vector Form of the above equation:

$F=i \left(\overrightarrow{l} \times \overrightarrow{B} \right) $

Alternative Method

Let us consider, a conductor of length of $l$ in which $i$ current carrying is flowing and placed in magnetic field $B$ at an angle $\theta$. If $i$ current is flowing in the conductor then magnetic force on the conductor depends upon

1) The magnetic force is directly proportional current.

$F \propto i \qquad(1)$

2.) The magnetic force is directly proportional to the length of the conductor.

$F \propto l \qquad(2)$

3.) The magnetic force is directly proportional to the magnetic field.

$F \propto B \qquad(3)$

4.) The magnetic force is directly proportional to the $sin \theta$. Here $\theta$ is the angle between the length of the current element and the magnetic field.

$F \propto sin \theta \qquad(4)$

from equation $(1)$, $(2)$, $(3)$, and equation $(4)$

$F \propto i \: l \: B sin\theta$

$F = k \: i \: l \: B sin\theta$

Here $k$ is constant which has value $1$, then above equation

$F = i\: l \: b \: sin\theta$

Vector form of the above equation:

$F = i \left( \overrightarrow{l} \times \overrightarrow{B} \right)$