Fraunhofer diffraction due to a single slit

Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is incident normally from $S$ on a narrow slit $AB$ of width $e$ and is diffracted from it. The diffracted beam is focused at the screen $XY$ by another converging lens $L_{2}$. The diffraction pattern having a central bright band followed by an alternative dark and bright band of decreasing intensity on both sides is obtained.

Analytical Explanation: The light from the source $S$ is incident as a plane wavefront on the slit $AB$. According to Huygens's wave theory, every point in $AB$ sends out secondary waves in all directions. The undeviated ray from $AB$ is focused at $C$ on the screen by the lens $L_{2}$ while the rays diffracted through an angle $\theta$ are focussed at point $p$ on the screen. The rays from the ends $A$ and $B$ reach $C$ in the same phase and hence the intensity is maximum.

Fraunhofer diffraction due to a single slit

Expression for intensity:

To find the intensity at $P$, Let us draw normal $AN$ on $BN$. Therefore the path difference between the extreme rays is

$\Delta=BN$

$\Delta=AB \: sin \theta$

$\Delta=e \: sin \theta \qquad(1)$

Where $AB=e$ (width of the slit)

The phase difference

$\Delta \phi =\frac{2 \pi}{\lambda} e \: sin\theta \qquad(2)$ {from eq$(2)$}

Let AB be divided into a large number $n$ of equal parts then there may be an infinitely large number of the point sources of secondary wavelets between $A$ and $B$. The phase difference between any two consecutive parts is, therefore

$\frac{1}{n} \Delta \phi=\frac{1}{n} \frac{2 \pi}{\lambda} e \: sin\theta$

According to the theory of the composition of $n$ vibration each of amplitude $a$ and common phase difference $\delta$ between successive vibrations, the resultant amplitude at $P$ is given by

$R=a\frac{sin(\frac{n\delta}{2})}{sin(\frac{\delta}{2})} \qquad(4)$

Put the value of $\delta$ in equation $(4)$ so

$R=a \frac{sin [(\frac{1}{n} \frac{2\pi}{\lambda}e\: sin \theta) \frac{n}{2}]}{sin [\frac{1}{2}(\frac{1}{n} \frac{2\pi}{\lambda}e\: sin \theta)]}$

$R=a \frac{sin (\frac{\pi}{\lambda}e\: sin \theta)}{sin [\frac{1}{n} (\frac{\pi}{\lambda}e\: sin \theta)]} \qquad(5)$

Let $\alpha=\frac{\pi}{\lambda}e\: sin \theta \qquad(6)$

Then from equation $(5)$

$R=a \frac{sin \alpha }{sin (\frac{\alpha}{n})} \qquad(7)$

For the large value of $n$, the value of $\frac{\alpha}{n}$ is very small, Therefore $sin \alpha \approx \frac{\alpha}{n}$

Then equation $(7)$ can be written as

$R=a \frac{sin \alpha}{\frac{\alpha}{n}}$

$R=\frac{na \: sin\alpha}{\alpha}$

$R=\frac{A \: sin\alpha}{\alpha} \qquad(8)$

Where $A$ is total amplitude of $n$ vibration.$R$ is resultant amplitude of $n$ vibration

So the resultant intensity at $P$

$I=R^{2}$

$I=\frac{A^{2} \: sin^{2}\alpha}{\alpha^{2}} \qquad(9)$

Condition for Principle Maxima:

From equation $(7)$

$R=\frac{A \: sin\alpha}{\alpha}$

$R=\frac{A}{\alpha} [\alpha - \frac{\alpha^{3}}{3!} + \frac{\alpha^{5}}{5!} -\frac{\alpha^{7}}{7!} + ..... ]$

$R=A [1 - \frac{\alpha^{2}}{3!} + \frac{\alpha^{4}}{5!} -\frac{\alpha^{6}}{7!} + .....] $

If $\alpha=0$ then the resultant amplitude will be maximum then

$R=A$

And

$\frac{\pi}{\lambda}e\: sin \theta = 0$ {From equation $(6)$}

$sin \theta = 0$

$sin \theta = sin 0^{\circ}$

$ \theta = 0^{\circ}$

The resultant intensity at $P$ will be the maximum. For $\theta=0^{\circ}$ and called the principal maxima. Hence the intensity of the principal maxima:

$I_{0}=A^{2}$

Condition for Minima:

It is clear from equation $(8)$ that the intensity will be minimum when $sin\alpha=0$ but $\alpha \neq 0$ So.

$sin \alpha =0$

$sin \alpha= sin (m \pi)$

$\alpha=\pm m \pi$

And

$\frac{\pi}{\lambda}e\: sin \theta = \pm m \pi$ {From equation $(6)$}

$\frac{\pi}{\lambda}e\: sin \theta = \pm m \pi$

$ e\: sin \theta = \pm m \lambda$

The value of $m=1,2,3,4,5,......$ gives the direction of first, second, third,.....minima.

Condition for Secondary Maxima: In the diffraction pattern, there are secondary maxima in addition to principal maxima. The condition of secondary maxima may be obtained by differentiating equation $(9)$ with respect to $\alpha$ and equating it to zero. Hence

$\frac{dI}{d\alpha}=\frac{d}{d\alpha} \left( A^{2} \frac{sin^{2}\alpha}{\alpha^{2}}\right)$

$\frac{dI}{d\alpha}=A^{2} 2 \left(\frac{sin\alpha}{\alpha} \left [\frac{\alpha \: cos\alpha - sin\alpha}{\alpha^{2}} \right ] \right)$

But for maxima $\frac{dI}{d\alpha}=0$

So $A^{2} 2 \left(\frac{sin\alpha}{\alpha} \left [\frac{\alpha \: cos\alpha - sin\alpha}{\alpha^{2}}\right ] \right)=0$

$ \frac{\alpha \: cos\alpha - sin\alpha}{\alpha^{2}}=0$

$\alpha \: cos\alpha - sin\alpha=0$

$\alpha=tan\alpha$

The above equation can be solved graphically by plotting the curves

$y=\alpha$

$y=tan\alpha$

The equation $y=\alpha$ gives the straight line passing through the origin and making an angle $45^{\circ}$ with the x-axis.

Position of maxima due to diffraction from a single slit

The point of intersection of these two curves gives the value of $\alpha$ satisfying the equation $\alpha=tan\alpha$. These points correspond to the value of

$\alpha= 0, \frac{\pm 3\pi}{2}, \frac{\pm 5\pi}{2}, \frac{\pm 7\pi}{2}, ................$

The first value $\alpha=0$ gives the position of principle maxima while the value of $\alpha= \frac{\pm 3\pi}{2}, \frac{\pm 5\pi}{2}, \frac{\pm 7\pi}{2}, ................$ gives the position first secondary maxima, second secondary maxima, and third secondary maxima and so on respectively.

The intensity of the first secondary maxima

$I_{1}=A^{2} \left [\frac{sin \left(\frac{3\pi}{2} \right)}{\frac{3\pi}{2}} \right ]^{2}$

$I_{1}=\frac{4}{9\pi^{2}}A^{2}=\frac{A^{2}}{22}=\frac{I_{0}}{22}$

Similarly, the intensities of secondary maxima

$I_{2}=A^{2} \left [\frac{sin \left(\frac{5\pi}{2} \right)}{\frac{5\pi}{2}} \right ]^{2}$

$I_{2}=\frac{4}{25\pi^{2}}A^{2}=\frac{A^{2}}{62}=\frac{I_{0}}{62}$

Thus, It is obvious from the value of $I_{0}, I_{1}, I_{2},.....$, etc that the diffraction pattern consists of a bright central maximum followed by minima of zero intensity and then secondary maxima of decreasing intensity on either side of it.

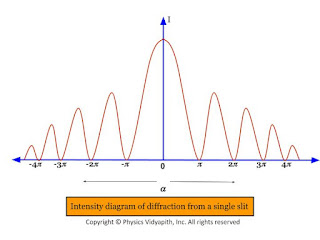Intensity diagram of diffraction from a single slit

It is also obvious from the value of $I_{0}, I_{1}, I_{2},.....$, etc that the relative intensities of successive maxima are nearly

$I_{0}: I_{1}: I_{2}:...=1:\frac{4}{9\pi^{2}}: \frac{4}{25\pi^{2}}: \frac{4}{49\pi^{2}}:...$