Electric Potential:
When a test-charged particle is brought from infinity to a point in the electric field then the work done per unit test charge particle is called
electric potential. It is represented by $V$. It is a scalar quantity.
Let's consider a test-charged particle $q_{0}$ bring from infinity to at a point $P$ in the electric field. If the work done by test charged particle is $W$ then electric potential →
$V=\frac{W}{q_{0}}$
Unit of Electric Potential: $Joul/Coulomb$ OR $N-m/Ampere-sec$
In MKS: $Kg-m^{2}-Ampere^{-1}-sec^{-3}$
Dimension of Electric potential: $[ML^{2}A^{-1}T^{-3}]$
The electric potential at a point due to point charged particle:
Let us consider, a source point charge $+q$ is placed in air and vacuum at point $O$.Let's take a point $P$ at distance $r$ from the source point charged particle. Here the test-charged particle $+q_{0}$ is brought from infinity to point $P$.If the test-charged particle moves a very small distance $dx$ from point $A$ to $B$ against the electrostatic force. So electrostatic force at point $A$ which is placed at a distance $x$ from point $O$ →
$F=\frac{1}{4\pi\epsilon{0}} \frac{qq_{0}}{x^{2}} \qquad(1)$
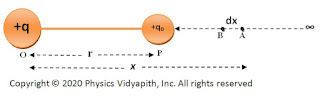 |
| Electric potential due to point charge |
The work is done against the electrostatic force $\overrightarrow{F}$ to move small distance $dx$ from point $A$ to Point $B$
$ dW=\overrightarrow{F}\: \overrightarrow{dx}$
$ dW=F\: dx \: cos 180^{\circ}$
Here the angle between the electrostatic force and displacement is $180^{\circ}$. So work done
$ dW=- F\: dx$
$ dW=-\frac{1}{4\pi\epsilon{0}} \frac{qq_{0}}{x^{2}}\:dx \qquad \left\{ from\: equation \: (1) \right\}$
The total work is done in moving the charge $q_{0}$ from infinity to the point $P$ will be
$W=-\int_{0}^{W}{dW}$
Here negative sign shows that the work done from infinity to at point $P$ is stored in the form of potential energy between the charges.
$ W=-\int_{\infty}^{r}{\frac{1}{4\pi\epsilon{0}} \frac{qq_{0}}{x^{2}}\:dx }$
$ W=-\frac{qq_{0}}{4\pi\epsilon{0}} \int_{\infty}^{r}{\frac{dx}{x^{2}} }$
$W=-\frac{qq_{0}}{4\pi\epsilon{0}} \left [\frac{-1}{x} \right ]_{\infty}^{r}$
$ W=-\frac{qq_{0}}{4\pi\epsilon{0}} \left [-\frac{1}{r}-\frac{-1}{\infty} \right ]$
$W=\frac{qq_{0}}{4\pi\epsilon{0}} \left [\frac{1}{r} \right ]$
$ W=\frac{1}{4\pi\epsilon{0}} \left [\frac{qq_{0}}{r} \right ]$
Hence, the work is done to move a unit test charge from infinity to the point $P$, or the electric potential at point $P$ is →
$V=\frac{W}{q_{0}}$
$V=\frac{1}{4\pi\epsilon{0}} \frac{q}{r}$





