Principle of continuity in fluid
Statement of Principle of Continuity:
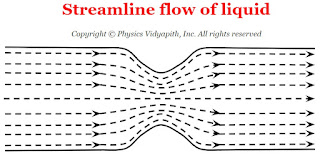
When an ideal liquid (i.e. incompressible and non-viscous liquid ) flows in streamlined motion through a tube of non-uniform cross-section, then the product of the velocity of flow and area of cross-section is always constant at every point in the tube.
Mathematical Analysis (Proof)
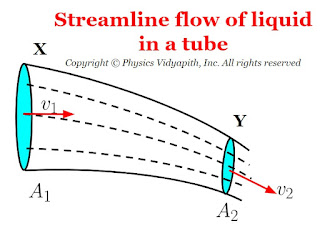
Let us consider, an ideal liquid (i.e. incompressible and non-viscous liquid ) flow in streamline motion through a tube $XY$ of the non-uniform cross-section.
Now Consider:
The Area of cross-section $X = A_{1}$
The Area of cross-section $Y = A_{2}$
The velocity per second (i.e. equal to distance) of fluid at cross-section $X = v_{1}$
The velocity per second (i.e. equal to distance) of fluid at cross-section $Y = v_{2}$
The volume of liquid entering at the cross-section $X$ in $1$ second is = $A_{1}v_{1}$
The mass of liquid entering at the cross-section $X$ in $1$ second is = $ \rho A_{1}v_{1}$
Similarly, the mass of the liquid coming out from the cross-section $Y$ in $1$ second is = $ \rho A_{2}v_{2}$
But the liquid which enters at cross-section $X$ must leave cross-section $Y$. Hence the masses are equal at both cross-section area, that is,
$\rho A_{1}v_{1} = \rho A_{2}v_{2} $
$ A_{1}v_{1} = A_{2}v_{2} $
$A v = constant$
Thus, the above equation shows that at every place in the tube, the product of the area of the cross-section of the tube and the velocity of the flow of the liquid is always the same. Therefore, the velocity of the liquid is smaller in the wider parts of the tube and larger in the narrow parts.