Power in Alternating Current Circuit

Definition of Power in Alternating Current Circuit:

The rate of power consumption in an alternating current circuit is known as power in the circuit.

Mathematical Analysis:

Let us consider an alternating current circuit in which the voltage and current at any instant are given by

$V=V_{\circ} sin \omega t \qquad(1)$

$i=i_{\circ} sin \left( \omega t - \phi \right) \qquad(2)$

Where $\phi$ $\rightarrow$ Phase difference between voltage and current

So instantaneous Power

$P=Vi$

$P=\left\{V_{\circ} sin \omega t \right\} \left\{ i_{\circ} sin \left( \omega t - \phi \right) \right\}$

$P=V_{\circ} i_{\circ} \: sin \omega t \: sin \left( \omega t - \phi \right)$

$P=\frac{V_{\circ} i_{\circ}}{2} \left[2\: sin \: \omega t \: sin \left( \omega t - \phi \right)\right]$

$P=\frac{V_{\circ} i_{\circ}}{2} \left[ cos \left( \omega t -\omega t + \phi \right) \\ \qquad - cos \left( \omega t + \omega t - \phi \right) \right]$

$P=\frac{V_{\circ} i_{\circ}}{2} \left[ cos \left(\phi \right) - cos \left( 2\omega t - \phi \right) \right]$

The average power for one cycle is:

$P_{avg}$ = The average value of $\left\{ \frac{V_{\circ} i_{\circ}}{2} \left[ cos \left(\phi \right) - cos \left( 2\omega t - \phi \right) \right] \right\}$

The term $cos \left( 2\omega t - \phi \right)$ is time-dependent and the average value of term $cos \left( 2\omega t - \phi \right)$ for complete one cycle is zero. So the average power dissipation in one cycle is

$P_{avg}= \frac{V_{\circ} i_{\circ}}{2} cos \phi $

$P_{avg}= \frac{V_{\circ}}{\sqrt{2}} \frac{i_{\circ}}{\sqrt{2}} cos \phi $

$P_{avg}= V_{rms} \: i_{rms} cos \phi $

Case -1 The circuit containing Pure Resistor only:

If the circuit contains a pure resistance only then voltage $V$ and current $i$ are always in the same phase. i.e. $\phi=0^{\circ}$ and $cos \phi = +1$, then average power

$P_{avg}= V_{rms} \: i_{rms} $

Case -2 The circuit containing Pure Inductor only:

If the circuit containing pure inductor only then voltage $V$ leads over current $i$ by $90^{\circ}$ i.e. $\phi=90^{\circ}$ and $cos 90^{\circ} = 0$, then average power

$P_{avg}= 0 $

Case -3 The circuit containing Pure Capacitor only:

If the circuit containing pure capacitor only then voltage $V$ lags behind current $i$ by $90^{\circ}$ i.e. $\phi=90^{\circ}$ and $cos 90^{\circ} = 0$, then average power

$P_{avg}= 0 $

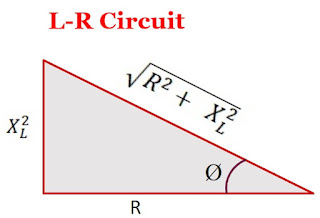
Case -4 The circuit containing inductor and resistor only (L-R Circuit):

We know that the phase in the L-R circuit is

$tan \phi = \frac{X_{L}}{R}$

From the above equation, Draw the triangle as shown in the figure below:

From the above figure, the value of $cos\phi$ is

$cos \phi = \frac{R}{\sqrt{R^{2} + X^{2}_{L}}}$

So average power

$P_{avg}= V_{rms} \: i_{rms} \frac{R}{\sqrt{R^{2} + X^{2}_{L}}} $

$\left(P_{avg}\right)_{L-R} \lt \left(P_{avg}\right)_{R}$

Thus, the average power consumption in an L-R circuit is less than the power consumed in a purely resistive circuit

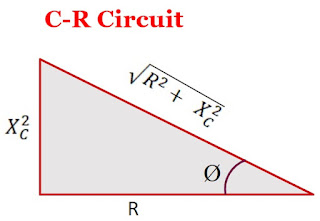
Case -5 The circuit containing capacitor and resistor only (C-R Circuit):

We know that the phase in the C-R circuit is

$tan \phi = \frac{X_{C}}{R}$

From the above equation, Draw the triangle as shown in the figure below:

From the above figure, the value of $cos\phi$ is

$cos \phi = \frac{R}{\sqrt{R^{2} + X^{2}_{C}}}$

So average power

$P_{avg}= V_{rms} \: i_{rms} \frac{R}{\sqrt{R^{2} + X^{2}_{C}}} $

$\left(P_{avg}\right)_{C-R} \lt \left(P_{avg}\right)_{R}$

Thus, the average power consumption in a C-R circuit is less than the power consumed in a purely resistive circuit

Case -6 The circuit containing capacitor and inductor only (L-C Circuit):

We know that the phase in the L-R circuit is

$\phi = 90^{\circ}$ and $cos 90^{\circ} = 0$

So average power

$P_{avg}= 0 $

Case -7 The circuit containing inductor, capacitor, and resistor only (L-C-R Circuit):

We know that the phase in the L-C-R circuit is

$tan \phi = \frac{X_{L} - X_{C}}{R}$

From the above equation, Draw the triangle as shown in the figure below:

From the above figure, the value of $cos\phi$ is

$cos \phi = \frac{R^{2}}{\sqrt{R^{2} + \left( X^{2}_{L} - X^{2}_{C} \right) }}$

So average power

$P_{avg}= V_{rms} \: i_{rms} \frac{R^{2}}{\sqrt{R^{2} + \left( X^{2}_{L} - X^{2}_{C} \right) }} $

$\left(P_{avg}\right)_{L-C-R} \lt \left(P_{avg}\right)_{R}$

Thus, the average power consumption in an L-C-R circuit is less than the power consumed in a purely resistive circuit

Wattless Current:

If the circuit contains only resistor or only inductor or only inductor and capacitor then power consumption in the circuit will be zero (i.e. there will be no energy dissipation in the circuit) due to the phase difference $90^{\circ}$ between voltage(or impedance) and current. So the current in the circuit is called the "Wattless current".