Description:
The motion of any particle is depends upon the force applying on it. In the magnetic field, the motion of charge is perpendicular to the magnetic force applied on the charge particle because of that the path of the charge particle becomes circular. If the direction of force and the direction of motion are not perpendicular to each other that is they are at any angle then the path of the charge particle becomes becomes helical.
A.) When $\overrightarrow{v}$ is perpendicular to $\overrightarrow{B}$→
Let us consider a charge $q$ enters in the magnetic field $\overrightarrow{B}$ from a point $O$ with velocity $\overrightarrow{v}$ directed perpendicular to the magnetic field $\overrightarrow{B}$.The general Expression for the force acting on the particle is
$\overrightarrow{F}=q(\overrightarrow{v} \times \overrightarrow{B})$
Here the magnetic field $\overrightarrow{B}$ is perpendicular to the plane of the page directed downwards which is shown in the figure below.
Since the velocity of charge particle $\overrightarrow{v}$ is perpendicular to the magnetic field $\overrightarrow{B}$ then the magnitude of the force $F$ will be
$F=qvB \qquad(1)$
Since the force is perpendicular to the velocity and the direction of velocity continuously changes but the magnitude of velocity is not changing. Therefore the particle will move in a circular path with constant speed in a uniform magnetic field and the magnetic force will act as a centripetal force. i.e.
$F=\frac{m v^{2}}{r} \qquad(2)$
Where
$r$ → Radius of the circular path
$m$ → mass of the particle
From equation $(1)$ and equation $(2)$
$\frac{m v^{2}}{r}=qvB$
$r=\frac{mv}{qB}$
The direction of the path of the particle depends upon the nature of the charge and the direction of the magnetic field.
The particle travels a distance $2\pi r$ in one revolution. So the time period of one revolution is
$T=\frac{2\pi r}{v} \qquad(3)$
Now substitute the value of $r=\frac{mv}{qB}$ in equation $(3)$ then we get
$T=\frac{2\pi m}{qB}$
The frequency of the particle $n=\frac{1}{T}$ can be written as
$n=\frac{qB}{2\pi m}$
From the above equations, We can conclude that the time period or frequency of the particle is independent of the speed $v$ of the particle. If the speed of the charge particle increases, its radius also increases so that the time taken to complete one cycle or revolution remains the same. If two identical charged particles enter the field with different speeds $v_{1}$ and $v_{2}$, then they move along the circle of smaller and larger radii respectively which is shown in the figure below.
 |
| The frequency and Time period of the particle are independent of the speed |
B.) When $\overrightarrow{v}$ is not perpendicular to $\overrightarrow{B}$→
Now, Again Let that the particle is entering with velocity $\overrightarrow{v}$ in the magnetic field $\overrightarrow{B}$, instead of being perpendicular to $\overrightarrow{B}$, makes angle $\theta (0 < \theta < 90^{\circ})$ with it. Now the velocity $\overrightarrow{v}$ may resolved into two components;
First is:
$v_{\parallel}=v \: cos\theta$ i.e. Parallel to magnetic field $\overrightarrow{B}$. This component gives the linear path to the particle.
Second is:
$v_{\perp}=v \: sin\theta$ i.e. Perpendicular to magnetic field $\overrightarrow{B}$. This component gives the circular path to the particle.
The resultant of these two-component gives the helical path to the particle whose axis is parallel to the magnetic field.
The radius of the circular path of the helix is
$r=\frac{mv_{\perp}}{qB}$
$r=\frac{mv \: sin\theta}{qB}$
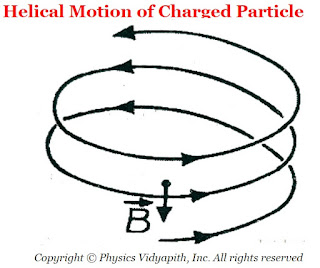 |
| Helical Motion of Charged Particle |
The time period of the particle
$T=\frac{2\pi m}{qB}$
The linear distance traveled by the particle in the direction of the magnetic field in one complete circle is called the 'pitch $(p)$' of the path.
$p=v_{\parallel} \times T$
$T= v \: cos\theta \times \frac{2\pi m}{qB}$
Kinetic Energy of Charged Particle Moving in Uniform Magnetic Field→
The kinetic energy is
$K=\frac{1}{2}mv^{2}$
$K=\frac{(mv)^{2}}{2m}$
Now substitute the value of $mv$ from
$r=\frac{mv}{qB}$. Then we get
$K=\frac{1}{2}m \left( \frac{rqB}{m} \right)^{2}$
$K=\frac{r^{2}q^{2}B^{2}}{2m}$



