Newton's Corpuscular Model

Newton's Corpuscular Theory

In the year 1675, Newton proposed the corpuscular theory of light to explain the existing phenomenon of light. There are the following assumptions of this theory:

1. The light consists of very small, lightweight, and invisible particles. These particles are known as corpuscles.

2. These corpuscles move with the velocity of light in a homogeneous medium in all possible directions in a straight line and they carry kinetic energy with them.

3. When these corpuscles fall on the retina of the eye, they produce the sensation of vision.

4. The size of corpuscles of different colors is different (ie, the color of light depends on the size of the corpuscle).

(A) Success of Carpuscles Theory

Based on this theory, the following facts related to light were explained successfully:

1. The light has energy: Since corpuscles have kinetic energy. Therefore, the energy of the light beam is due to the kinetic energy of the corpuscles.

2. Motion of light along a straight line: Since velocity of the corpuscle is very high, the effect of external forces on it is negligible. Therefore, it moves in a straight line.

3. Motion of light in vacuum: Corpuscles can move through vacuum.

4. Reflection of light: To explain the reflection of light, Newton assumed that when a corpuscle reaches close to a reflecting surface, then the surface repels it with a force whose direction is perpendicular to the surface and whose magnitude decreases sharply as the distance of corpuscles increases from the surface.

In Figure, let $PO$ be a reflecting surface and $P'Q'$ be an imaginary surface just above it at negligible height. When a light corpuscle moves towards the surface, then it moves along a straight line from $A$ to $B$ (since the force is zero). As it reaches the point $B$ of surface $PQ$, a repulsive force starts acting perpendicular to the surface (upward in the figure). Let $i$ is an angle of incidence at point $B$, then the velocity of the corpuscles at point $B$ has two components- component parallel to surface $V_{||} =v \: sin \: i$ and component perpendicular to surface $V_{|} = v \: cos \: i$. After crossing point $B$, the parallel component remains same but the perpendicular component decreases. At point $C$ of surface $PQ$, the perpendicular component becomes zero. After this direction of the perpendicular component changes and the corpuscles move along path CD. Beyond D again it moves along a straight line as the force becomes ineffective. If $r$ is the angle of reflection at point $D$, then the parallel component of velocity at $D$ will be $v\: sin\: r$. Since the parallel component remains constant. Therefore, comparing them at points $B$ and $D$.

$v \: sin \: i=v \: sin\: r$

$sin \: i= sin\: r$

$i=r$

i.e., the above equation shows that the incident angle and the reflected angle are equal. In the figure above, incident ray, reflected ray and normal all three are in the plane of paper. Therefore laws of reflection are verified.

5. Refraction of light: To explain the refraction of light, Newton considered two different situations :

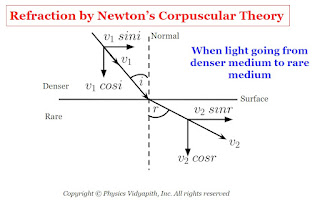
a.) When the light goes from a denser medium to a rare medium: In this condition when the corpuscle reaches near the surface, the surface exerts a normal repulsive force on it. As a result, the perpendicular component of velocity of the corpuscles decreases however it does not reduce to zero as in the case of refraction. Therefore, enters the second medium with a reduced perpendicular component and same constant value of the parallel component i.e., moves along a straight line bending away from normal.

If $i$ and $r$ are the angle of incidence and angle of refraction and $v_{1}$ and $v_{2}$ are the velocity of corpuscle in medium first and second medium. If the parallel component is constant,

$v_{1} \: sin \: i =v_{2} \: sin\: r$

$\frac{sin \: i}{sinr} =\frac{v_{2}}{v_{1}}$

From Figure

$i \lt r$

Therefore

$sin \: i \lt sin\: r$

$v_{2} \lt v_{1}$

Therefore, from the corpuscular theory, velocity light in a denser medium ($v_{1}$) is greater than the velocity light in a rare medium ($v_{2}$).

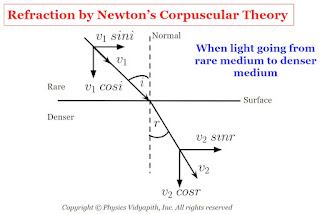
b.) When the light goes from a rare medium to a denser medium: In this condition when the corpuscle reaches near to the surface, the surface attracts it normally. As a result, the normal component of its velocity increases. Therefore, the corpuscular enters the second medium with an increased normal component and the same parallel component of velocity and moves along a straight line bending towards the normal. 

$v_{1} \: sin \: i =v_{2} \: sin\: r$

$\frac{sin \: i}{sinr} =\frac{v_{2}}{v_{1}}$

From Figure

$i \gt r$

Therefore

$ sin \: i \gt sin\: r$

$v_{2} \gt v_{1}$

Therefore, velocity light in a denser medium ($v_{1}$) is greater than the velocity light in a rare medium ($v_{2}$).

B) Failure of the Corpuscles Theory

The following are the main reasons for the failure of this theory:

1. Interference, diffraction, polarisation of light, and the photoelectric effect, etc. can not be explained using this principle. For example, in interference, when two light beams interfere, darkness is produced at the same places. It is not possible that two corpuscles destroy each other.

2. According to this theory, the velocity of light is greater in the denser medium as compared to the rare medium. But Focault's had proved experimentally that the velocity of light is less in denser mediums as compared to the velocity of light in rare mediums.

3. According to this theory, greater the temperature of the source greater the velocity of the corpuscles. Actually, the velocity of light does not depend on the temperature of the source.

4. According to this theory, the mass of the source should decrease as it continuously emits corpuscles but it does not happen in reality.

5. In this theory two opposite assumptions are considered to explain reflection and refraction. To explain reflection and refraction through denser to rarer, the repulsive force by the surface is assumed and to explain refraction from rare to denser, the force of attraction by the surface is assumed. These assumptions are opposite and they don't have any scientific base.