Combination of cell in the circuit

A.) Combination of cells when emf of cells are same: There are three types of combinations of cells in the circuit

1.) Series Combination of Cells

2.) Parallel Combination of Cells

3.) Mixed Combination of Cells

1.) Series Combination of Cells: Let us consider that the $n$ - cells having emf (electromotive force) $E$ and internal resistance $r$ are connected in series with external resistance $R$. Then from the figure given below

The total emf of the $n$ - cell = $nE$

The total internal resistance of the $n$ - cell = $nr$

The total resistance of the circuit = $nr+R$

The total current in the circuit

$i=\frac{Total \: emf \: of \: the \: n - series \: cell}{Total \: resistance \: of \: the \: circuit}$

$i=\frac{nE}{nr+R}$

2.) Parallel Combination of Cells: Let us consider that the $n$ - cells having emf (electromotive force) $E$ and internal resistance $r$ are connected in parallel with external resistance $R$. Then from the figure given below

The total emf of the $n$ - cell = $E$

The total internal resistance of the $n$ - cell

$\frac{1}{r_{eq}} = \frac{1}{r}+ \frac{1}{r}+.........n \: times$

$\frac{1}{r_{eq}}=\frac{n}{r}$

$r_{eq}=\frac{r}{n}$

The total resistance of the circuit = $\frac{r}{n}+R$

The total current in the circuit

$i=\frac{Total \: emf \: of \: the \: n - parallel \: cell}{Total \: resistance \: of \: the \: circuit}$

$i=\frac{E}{\frac{r}{n}+R}$

$i=\frac{E}{\frac{r+nR}{n}}$

$i=\frac{nE}{r+nR}$

3.) Mixed Combination of Cells: Let us consider that the $n$ - cells having emf (electromotive force) $E$ and internal resistance $r$ are connected in series in each row of $m$ parallel rows with external resistance $R$. Then from the figure given below

The total emf of the $n$ - cell in each row of $m$ parallel rows of the cells = $nE$

The internal resistance of the $n$ - cell in each row = $nr$

The total internal resistance of the $n$ - cell in each of $m$ parallel rows of the cells = $nr$

$\frac{1}{r_{eq}} = \frac{1}{nr}+ \frac{1}{nr}+.........m \: times$

$\frac{1}{r_{eq}}=\frac{m}{nr}$

$r_{eq}=\frac{nr}{m}$

The total resistance of the circuit = $\frac{nr}{m}+R$

The total current in the circuit

$i=\frac{Total \: emf \: of \: the \: cell}{Total \: resistance \: of \: the \: circuit}$

$i=\frac{nE}{\frac{nr}{m}+R}$

$i=\frac{nE}{\frac{nr+mR}{m}}$

$i=\frac{mnE}{nr+mR}$

It is clear from the above equation that for the value of $i$ to be maximum, the value of $(nr+mR)$ should be minimum. Now,

$nr+mR= \left[ \sqrt{nr}-\sqrt{mr} \right]^{2}+2 \sqrt{mnRr}$

Therefore, for $(nr+mR)$ to be minimum, the quantity $\left[ \sqrt{nr}-\sqrt{mr} \right]^{2}$ should be minimum. So

$\left[ \sqrt{nr}-\sqrt{mr} \right]^{2} = 0$

$ \sqrt{nr}-\sqrt{mr} = 0$

$ \sqrt{nr} = \sqrt{mr} $

$nr=mR$

$R=\frac{nr}{m}$

Here, $\frac{nr}{m}$ is the total resistance of the cells.

Thus, When the total internal resistance of the cells are equal to the external resistance then the total current in the external circuit will be maximum in the mixed combination of cells.

Read More

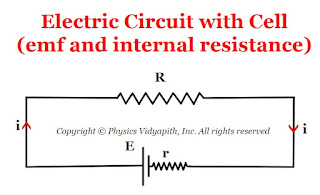
Relation between electromotive force (E), internal resistance (r) and potential difference (V) in a circuit

Relation between electromotive force $(E)$, internal resistance $(r)$ and potential difference $(V)$:

Let us consider:

The cell having electro-motive force = $E$

The cell having internal resistance = $r$

The external resistance of the circuit = $R$

The potential difference between the external resistance of the circuit = $V$

The current in circuit = $i$

So, The emf of the cell from the given circuit in the figure above

$E=iR+ir$

$E = V+ir$

$V=E-ir$

Read More

Resolving Power of Optical Instrument | Rayleigh Criterion of Resolution

Resolving power of an optical instrument:

The ability of an optical instrument to just resolve the images of two closely spaced objects is called its resolving power.

Limit of Resolution:

The smallest distance between two closely spaced objects that can be seen as separated or just separated from each other through an optical instrument is known as the limit of resolution of that optical instrument.

Rayleigh Criterion:

Rayleigh criterion describes the separation between the two objects or wavelengths (i.e. resolving power) by the resultant intensity distribution of objects and wavelengths. According to Rayleigh's criterion, there are the following cases:

Case:1 If two point sources have very small angular separation, then central or principal maxima in their diffraction patterns will overlap to a large extent and resultant intensity shows uniform variation. As shown in the figure below. In this case, the two objects or wavelengths can not be distinguished or unresolved.

Case:2 If two point sources have very large angular separation then the central or principal maxima are widely separated and the resultant intensity shows two widely separated peaks. As shown in the figure below. In this case, the objects or wavelengths are resolved well.

Case:3 If the central or principal maxima in the diffraction pattern of one object or wavelength coincide with the first minima in the diffraction pattern of the other objects or wavelength then the resultant intensity shows a small dip. As shown in the figure below. In this case, the objects or wavelengths are seen to be just separate or just resolved.

Read More