Description→
When a capacitor is charged, the work is done by charged battery (i.e the chemical energy of the battery is used to charge the capacitor). As the capacitor gets charged, the potential difference between its plates increases. Due to this increase in the potential difference between the plates, the battery has to give the same amount of charge to the capacitor. Because of that, the battery has to do more and more work.
The total amount of work done in charging the capacitor is stored in the form of electric potential energy in between the capacitor plates. This energy is retrieved as heat when the capacitor is discharged through a resistance.
Derivation→
Let us consider, a capacitor of capacitance $C$with a potential difference of $V$ between the plates.
In the process of charging, electrons are transferred from the positive to negative, unit each plate acquires an amount of charge $q$. Suppose during the process of charging, we increase the charge from $q'$ to $q'+dq'$ by transferring an amount of negative charge $dq'$ from the positive to the negative plate. the work done
$dw=V' \: dq'$
$dw=\frac{q'}{C} \: dq'$
Therefore, the total work done in charging the capacitor from the uncharged state (i.e. zero charge in the capacitor) to the final charge $q$ will be
$W=\int_{0}^{W} dw$
$W=\int_{0}^{q} \frac{q'}{C} \: dq'$
$W=\frac{1}{2}\left[ \frac{q'^{2}}{C} \right]^{q}_{0} $
$W=\frac{1}{2}\left[ \frac{q^{2}}{C} \right]$
$W=\frac{1}{2}\:C \: V^{2}$
This work done is stored in the form of potential energy $U$ within the capacitor. Thus
$U=\frac{1}{2}\:C \: V^{2} $
$U=\frac{1}{2}\frac{q^{2}}{C}$
Energy Stored in Combination of Capacitor→
If many capacitors are combined in series, or in parallel, the total potential energy stored in either combination is equal to the sum of the potential energies stored in the individual capacitor. This follows from the combination of the capacitor's expressions:
The potential energy is stored in a series combination→
The potential energy stored in a series combination (here $q$ is constant) is
$U=\frac{1}{2}\frac{q^{2}}{C}$
For series combination the capacitance of capacitor i.e. $\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{2}}+..........$. Now substitute the value of $\frac{1}{C}$ in above equation
$U=\frac{1}{2}q^{2} \frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{2}}+.......... $
$U= \left( \frac{1}{2}q^{2} \frac{1}{C_{1}}+\frac{1}{2}q^{2} \frac{1}{C_{2}}+ \frac{1}{2}q^{2} \frac{1}{C_{2}}+.......... \right)$
$U=U_{1}+U_{2}+U_{3}+.........$
The potential energy is stored in a parallel combination→
The potential energy is stored in a parallel combination (here $V$ is constant) is
$U=\frac{1}{2}CV^{2}$
For parallel combination the capacitance of capacitor i.e. $C=C_{1}+C_{2}+C_{3}+......$. Now substitute the value of $C$ in the above equation
$U=\frac{1}{2} \left( C_{1}+C_{2}+C_{3}+........... \right) V^{2}$
$U= \frac{1}{2} C_{1} V^{2} + \frac{1}{2} C_{2} V^{2} +\frac{1}{2} C_{3}V^{2} +..... $
$U=U_{1}+U_{2}+U_{3}+......$
Force between the plates of a Charged Parallel Plate Capacitor
Derivation and Description→
Consider, A parallel plate capacitor with a charge $+q$ on one of its plates and $-q$ on the other plate. Let initially the plates of the capacitor are almost, but not quite touching. Due to opposite polarity, there is an attractive force $F$ between the plates. Now If these plates are gradually pulling and apart to a distance $d$, in such a way that $d$ is still small compared to the linear dimension of the plates, then the approximation of a uniform field between the plates is maintained and thus the force remains constant.
Now the work done in separating the plates from near $0$ to $d$,
$W=F.d \qquad(1)$
This work done $(W)$ is stored as electrostatic potential energy $(U)$ between the plates, i.e.
$U=\frac{1}{2}q V $
But $V=E.d$, then the above equation can be written as
$U=\frac{1}{2}q \: E \: d \qquad(2)$
But the equation $(1)$ and equation $(2)$ both are equal then
$F.d=\frac{1}{2}q \: E \: d$
$ F=\frac{1}{2}q \: E $
The factor $\frac{1}{2}$ arises because just outside the conducting plates the field is $E$ and inside the plates, the field is zero. So the average value $\frac{E}{2}$ contributes to the force.
 |
| The force between the charged parallel plates of the capacitor |
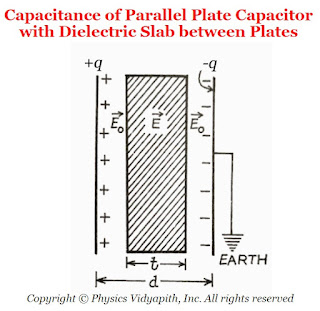
Capacitance of a Parallel Plate Capacitor Partly Filled with Dielectric Slab between Plates
Derivation→
Let us consider,
The charge on a parallel-plate capacitor = $q$
The area of parallel-plate = $A$
The distance between the parallel-plate = $d$
The dielectric constant of the slab of a material =$K$
The thickness of the material =$t$
The vacuum (or air) between the plates =$(d-t)$ The surface charge density on the plates= $\sigma$
The electric field in the air between the plates is
$E_{\circ}=\frac{\sigma}{\epsilon_{\circ}}$
$E_{\circ}=\frac{q}{\epsilon_{\circ}\: A} \qquad(1)$
The electric field in the dielectric material
$E=\frac{q}{\epsilon_{\circ}\: K\: A} \qquad(2)$
The potential difference between the plates
$V=E_{\circ}\left( d-t \right)+E\:t \qquad(3)$
Now substitute the value of $E_{\circ}$ and $E$ in the equation $(3)$, Then we get
$V=\frac{q}{\epsilon_{\circ}\: A} \left( d-t \right)+ \frac{q}{\epsilon_{\circ}\: K\: A} \:t $
$V=\frac{q}{\epsilon_{\circ}\: A} \left[ \left( d-t \right)+ \frac{t}{K} \right] \qquad$
The capacitance of the capacitor is
$C=\frac{q}{V}$
Now substitute the value of electric potential $V$ in the above equation then
$C= \frac{q}{\frac{q}{\epsilon_{\circ}\: A} \left[ \left( d-t \right)+ \frac{t}{K} \right]}$
$C= \frac{\epsilon_{\circ}\: A}{\left[ \left( d-t \right)+ \frac{t}{K} \right]} $
Since $K>1$, the 'effective' distance between the plates becomes less than $d$ and so the capacitance increases.
Special Cases→
The area of parallel-plate = $A$
The distance between the parallel-plate = $d$
The dielectric constant of the slab of a material =$K$
The thickness of the material =$t$
The vacuum (or air) between the plates =$(d-t)$ The surface charge density on the plates= $\sigma$
 |
| The capacitance of Parallel Plate Capacitor with Dielectric Slab between Plates |
- When the dielectric slab is completely filled between the parallel plates i.e. $t=d$ then the capacitance between the parallel plates
$C= \frac{K \: \epsilon_{\circ}\: A}{d}$
- When there is a vacuum (or air) between the parallel plates i.e. $t=0$, then the capacitance between the parallel plates
$C_{\circ}= \frac{ \epsilon_{\circ}\: A}{d}$
- When there is a slab of metal whose dielectric constant is infinity (K=∞). If the thickness of the slab is t between the parallel plates, then the capacitance between the parallel plates
$C= \frac{ \: \epsilon_{\circ}\: A}{d-t}$
- When the slabs of dielectric constants $K_{1},K_{2},K_{3},K_{4}...........$ and respective thickness $t_{1},t_{2},t_{3},t_{4},........$ is placed in the entire space between the parallel-plates, then the capacitance between the plates
$C=\frac{\epsilon_{\circ} A}{d- \left( t_{1}+t_{2}+t_{3}+.... \right)+ \left( \frac{t_{1}}{K_{1}}+\frac{t_{2}}{K_{2}}+\frac{t_{3}}{K_{3}}+....... \right)}$But $d=t_{1}+t_{2}+t_{3}+....$$C=\frac{\epsilon_{\circ} A}{ \left( \frac{t_{1}}{K_{1}}+\frac{t_{2}}{K_{2}}+\frac{t_{3}}{K_{3}}+..... \right)}$
Parallel Plate Air Capacitor and Its Capacitance
Parallel Plate Air Capacitor→
A parallel-plate capacitor consists of two long, plane, metallic plates mounted on two insulating stands and placed at a small distance apart in a vacuum (or air). The plates are exactly parallel to each other.
Derivation of the capacitance of parallel plate capacitor in the air→
Let us consider, Two plates $X$ and $Y$ are separated at a small distance $d$ in the vacuum (or air). If the area of plates is $A$ and the plates $X$ and $Y$ have charge $+q$ and $-q$ respectively. If the surface charge density on each plate is $\sigma$ then electric field intensity at a point between two parallel plates is
$E=\frac{\sigma}{\epsilon_{\circ}}$
$E=\frac{q}{\epsilon_{\circ}A}\qquad(1) \qquad (\because \sigma=\frac{q}{A}) $
The potential difference between the parallel plates capacitor in air (or vacuum) is
$V=E.d$
Now substitute the value of $E$ from equation$(1)$ in the above equation
$V=\frac{q}{\epsilon_{\circ}A}.d \qquad(2)$
The capacitance of the parallel plate capacitor in air (or vacuum) is
$C_{\circ}=\frac{q}{V} \qquad(3)$
From equation $(2)$ and equation $(3)$
$C_{\circ}=\frac{q}{\frac{q}{\epsilon_{\circ}A}.d}$
$C_{\circ}=\frac{\epsilon_{\circ}A}{d}$
If the space between the plates is filled with some dielectric medium of dielectric constant $K$, then the electric field between the plates is
$E=\frac{\sigma}{K \: \epsilon_{\circ}}$
The Potential difference between the parallel plates when dielectric medium $(K)$ is present between them
$V=\frac{q}{K \: \epsilon_{\circ} \: A}.d $
Now, The capacitance of the parallel-plate capacitor when the dielectric medium $(K)$ is present between them
$C=\frac{K\: \epsilon_{\circ} \: A}{d}$
 |
| Parallel Plate Air Capacitor |
Potential Energy of a Charged Conductor
Definition:
Derivation →
Let us consider, a conductor of capacitance $C$. If charge $+Q$ is given into small amount of $dq$ to the surface of the conductor. Then the work done will be
$dw=V\:dq \qquad(1) $
$dw=\frac{q}{C} \:dq \qquad \left (\because V=\frac{q}{C} \right)$
Therefore, as the amount of charge on the conductor will increase from $0$ to $Q$ that causes also increase in work done. So integrate the above equation for total work done
$ \int_{0}^{W} dw=\frac{1}{C} \int_{0}^{Q} q dq$
$W=\frac{1}{C} \int_{0}^{Q} q dq$
$W=\frac{1}{C} \left[ \frac{q^{2}}{2} \right]^{Q}_{0}$
$W=\frac{1}{2} \frac{Q^{2}}{C}$
This work is stored in the form of electric potential energy $U$. Then
$U=\frac{1}{2} \frac{Q^{2}}{C}$
$U=\frac{1}{2} C V^{2}$
$U=\frac{1}{2} Q V$
The work done in charging the conductor is stored as potential energy in the electric field in the vicinity of the conductor is called the potential energy of a charged conductor.
Capacitance of an Isolated Spherical Conductor
Derivation →
Let us consider an isolated spherical conductor of radius $a$ is placed in a vacuum or air. Let a charge $+q$ be given to the sphere and this charge is distributed uniformly on the surface of conducting sphere. Then the electric potential at the surface of the conducting sphere is
$V=\frac{1}{4\pi \epsilon_{\circ}} \frac{q}{a} \qquad(1)$
So the capacitance of the sphere
$C=\frac{q}{V} \qquad(2)$
Now substitute the value of $V$ in equation $(2)$ Then we get
$C=\frac{q}{\frac{q}{4\pi \epsilon_{\circ}a}}$
$C=4\pi \epsilon_{\circ}a$
Thus, The capacitance of a spherical conductor is directly proportional to its radius. i.e If the radius of conducting sphere is large then the sphere will hold a large amount of the given charge without running up too high a voltage.
Unit:
The unit of capacitance is "Farad" i.e. $F$
 |
| Capacitance of an Isolated Spherical Conductor |
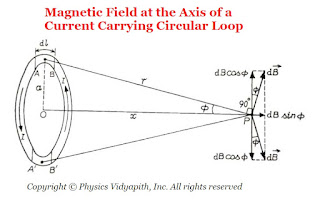
Magnetic Field at the axis of a current-carrying Circular Loop
Derivation→
Let us consider, A circular loop which have radius $a$, carrying a current $i$. Let take a point $P$ on the axis of the loop at a distance $x$ from the center $O$ of the loop.
Now to find the magnetic field at point $P$, take a small current element of length $dl$ at the top of the loop. Let $r$ is the distance between the current element and point $P$. Now apply the Biot-Savart's Law to find the magnitude of the magnetic field due to small current-element $dl$ at point $P$ i.e.
$dB=\frac{\mu_{\circ}}{4 \pi} \frac{i \: dl\: sin\theta}{r^{2 }}$
Where $\theta$ is the angle between the length of the element $dl$ and the line joining the element to the point $P$. Here this angle is $90^{\circ}$
$dB=\frac{\mu_{\circ}}{4\pi} \frac{i \: dl}{r^{2}}\qquad(1)$
The direction of the magnetic field $d\overrightarrow{B}$ is in the plane of the paper and at right angles to the line $r$ as shown in the figure below (By applying the right-hand screw rule). It can be resolved into two components, one is vertical component of magnitude $dB\: sin\phi$ along the axis of the loop and the other is horizontal component of magnitude $dB\: cos\phi$ at right angles to the axis.
Let us consider another current element of the same length at the bottom of the loop, directly opposite to the first element, which is at right angles to the plane of the page but directed inwards. the field due to $d\overrightarrow{B}$ but directed as shown in the figure above. It is clear that components of both the fields at right angles to the axis are equal and opposite. Hence they cancel each other. The component along the axis are in the same direction and so they are added up.
If we imagine the whole of the loop to be divided into such current elements, the resultant field $\overrightarrow{B}$ at $P$ is directed along the axis and its magnitude is given by
$B=\int dB \: \sin\phi$
Now substitute the value of $dB$ from equation $(1)$
$B=\int \frac{\mu_{\circ}}{4\pi} \frac{i \: dl}{r^{2}} \: \sin\phi$
From figure, $sin\phi=\frac{a}{r}$, we get
$dB=\int \frac{\mu_{\circ}}{4 \pi} \frac{i}{r^{2}} \frac{a}{r}dl$
$dB=\int \frac{\mu_{\circ}}{4 \pi} \frac{ia}{r^{3}} dl$
$dB= \frac{\mu_{\circ}}{4 \pi} \frac{ia}{r^{3}} \int dl$
$dB= \frac{\mu_{\circ}}{4 \pi} \frac{ia}{r^{3}} 2 \pi \: a \qquad \left( \int dl = 2 \pi \: a \right)$
$dB= \frac{\mu_{\circ}ia^{2}}{2r^{3}}$
Agian from figure $r^{2}=\left( a^{2} + x^{2}\right)^{3}$ or $r= \left( a^{2} + x^{2}\right)^{3/2}$. Now substitute the value of $r$ in above equation.
$B=\frac{\mu_{\circ}\: i\: a^{2}}{2(a^{2}+x^{2})^{3/2}}$
If it is a coil of $N$ turns, then each turn will contribute equally to $B$. Thus
$B=\frac{\mu_{\circ}\: N \: i \: a^{2}}{2(a^{2}+x^{2})^{3/2}}$
The direction of the magnetic field $\overrightarrow{B}$ is along the axis of the loop and that of the coil.
Magnetic field at the Centre of the Loop→
At the centre of the coil, we have $x=0$
$B=\frac{\mu_{\circ}\: N \: i}{2a}$
Again the direction of the magnetic field $\overrightarrow{B}$ is perpendicular to the plane of the coil i.e. Along the axis of the coil.
 |
| Magnetic Field at the Axis of a Current-Carrying Circular Loop |
Magnetic Field due to a Straight Current-Carrying Conductor of Finite Length
Derivation→
Let us consider, a current-carrying conductor $XY$ having length $l$ in which current $i$ is flowing from $X$ to $Y$. Now, To find the magnetic field due to the conductor, take a point $P$ at a distance $d$ from point $O$ of the conductor.
Now consider a small length element $dl$ at the conductor which is making an angle $\theta$ from point $P$. The length element $dl$ is also making the angle $d\theta$ from point $O$. If $\theta_{1}$ and $\theta_{2}$ is the angle from point $O$ to point $X$ and $Y$ respectively. Than magnetic field at point $P$ due to small length element $dl$ which is at a distance $r$
$dB=\frac{\mu_{0}}{4\pi} \frac{i\: dl \: sin (90+\theta)}{r^{2}}$
$dB=\frac{\mu_{0}}{4\pi} \frac{i \: dl \: cos\theta}{r^{2}} \qquad(1)$
But from the figure, In $\Delta NOP$
$cos\theta=\frac{d}{r}$
$r=\frac{d}{cos\theta} \qquad(2)$
$tan\theta=\frac{l}{d}$
$l=d\:tan\theta$
Now differentiate the above equation with respect to $\theta$, then
$dl=d \: sec^{2}\theta \: d\theta \qquad(3)$
Now substitute the value of $dl$ and $r$ from equation$(2)$ and equation $(3)$ in equation$(1)$, then we get
$dB=\frac{\mu_{o}i}{4\pi}\frac{d \:sec^{2}\theta \: d\theta \: cos\theta}{\frac{d^{2}}{cos^{2}\theta}}$
$dB=\frac{\mu_{o}i}{4\pi}\frac{sec^{2}\theta \: d\theta \: cos^{3}\theta}{d}$
$dB=\frac{\mu_{o}i}{4\pi}\frac{cos\theta \: d\theta}{d} \qquad(4)$
The magnitude of the magnetic field $\overrightarrow{B}$ at point $P$ due to the whole conductor $XY$ is
$B=\int_{-\theta_{1}}^{\theta_{2}}dB$
Now substitute the value of $dB$ in above equation so
$B=\int_{-\theta_{1}}^{\theta_{2}} \frac{\mu_{o}i}{4\pi}\frac{cos\theta \: d\theta}{d} $
$B=\int_{-\theta_{1}}^{\theta_{2}} \frac{\mu_{o}i}{4\pi d}cos\theta d\theta $
$B= \frac{\mu_{o}i}{4\pi d} \left[ sin\theta\right] _{-\theta_{1}} ^{\theta_{2}} $
$B= \frac{\mu_{o}i}{4\pi d} \left[ sin(\theta _{2}) - sin(-\theta_{1})\right] $
$B=\frac{\mu_{o}i}{4\pi d}\left( sin\theta _{1} + sin\theta_{2}\right) $
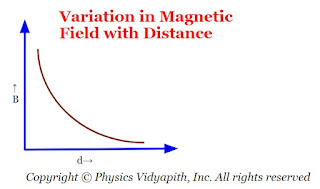
Special Case→
The variation of the magnitude of magnetic field $B$ with distance $d$ is shown in the figure below→
The line of force of magnetic field $\overrightarrow{B}$ near a linear current-carrying conductor are concentric circles of varying radii with their centers at the conductor in a plane perpendicular to the conductor. The direction of the magnetic field $\overrightarrow{B}$ at a point $P$, distant $d$, will be along the tangent drawn on a circle of radius $d$ around the conductor.
 |
| Magnetic Field due to a Straight Current-Carrying Conductor of Finite Length |
- For a conductor of infinite length, i.e $\theta_{1}=\theta_{2}=90^{\circ}$ then magnetic field
$B=\frac{\mu_{0}}{4\pi} \frac{2i}{d} $$B=\frac{\mu_{0}}{2\pi} \frac{i}{d} $
- If the point $P$ is at a distance $d$ near one end of the conductor,i.e. $\theta_{1}=90^{\circ}$ and $\theta_{2}=0$ then magnetic field
$B=\frac{\mu_{0}}{4\pi} \frac{i}{d} $From the above equations, we can conclude that the magnetic field $B$ at point $P$ is proportional to the current $i$ and inversely proportional to the distance $d$ of point $P$ from the conductor.
 |
| Variation in Magnetic field with distance |
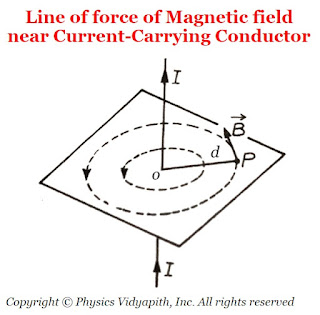 |
| Line of force of Magnetic field near Current-Carrying Conductor |
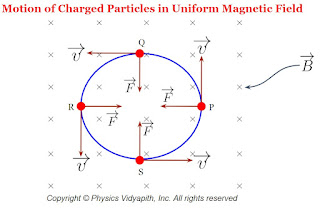
Motion of Charged Particles in Uniform Magnetic Field
Description:
The motion of any particle is depends upon the force applying on it. In the magnetic field, the motion of charge is perpendicular to the magnetic force applied on the charge particle because of that the path of the charge particle becomes circular. If the direction of force and the direction of motion are not perpendicular to each other that is they are at any angle then the path of the charge particle becomes becomes helical.
A.) When $\overrightarrow{v}$ is perpendicular to $\overrightarrow{B}$→
Let us consider a charge $q$ enters in the magnetic field $\overrightarrow{B}$ from a point $O$ with velocity $\overrightarrow{v}$ directed perpendicular to the magnetic field $\overrightarrow{B}$.The general Expression for the force acting on the particle is
$\overrightarrow{F}=q(\overrightarrow{v} \times \overrightarrow{B})$
Here the magnetic field $\overrightarrow{B}$ is perpendicular to the plane of the page directed downwards which is shown in the figure below.
Since the velocity of charge particle $\overrightarrow{v}$ is perpendicular to the magnetic field $\overrightarrow{B}$ then the magnitude of the force $F$ will be
$F=qvB \qquad(1)$
Since the force is perpendicular to the velocity and the direction of velocity continuously changes but the magnitude of velocity is not changing. Therefore the particle will move in a circular path with constant speed in a uniform magnetic field and the magnetic force will act as a centripetal force. i.e.
$F=\frac{m v^{2}}{r} \qquad(2)$
Where
$r$ → Radius of the circular path
$m$ → mass of the particle
From equation $(1)$ and equation $(2)$
$\frac{m v^{2}}{r}=qvB$
$r=\frac{mv}{qB}$
The direction of the path of the particle depends upon the nature of the charge and the direction of the magnetic field.
The particle travels a distance $2\pi r$ in one revolution. So the time period of one revolution is
$T=\frac{2\pi r}{v} \qquad(3)$
Now substitute the value of $r=\frac{mv}{qB}$ in equation $(3)$ then we get
$T=\frac{2\pi m}{qB}$
The frequency of the particle $n=\frac{1}{T}$ can be written as
$n=\frac{qB}{2\pi m}$
From the above equations, We can conclude that the time period or frequency of the particle is independent of the speed $v$ of the particle. If the speed of the charge particle increases, its radius also increases so that the time taken to complete one cycle or revolution remains the same. If two identical charged particles enter the field with different speeds $v_{1}$ and $v_{2}$, then they move along the circle of smaller and larger radii respectively which is shown in the figure below.
B.) When $\overrightarrow{v}$ is not perpendicular to $\overrightarrow{B}$→
Now, Again Let that the particle is entering with velocity $\overrightarrow{v}$ in the magnetic field $\overrightarrow{B}$, instead of being perpendicular to $\overrightarrow{B}$, makes angle $\theta (0 < \theta < 90^{\circ})$ with it. Now the velocity $\overrightarrow{v}$ may resolved into two components;
First is:
$v_{\parallel}=v \: cos\theta$ i.e. Parallel to magnetic field $\overrightarrow{B}$. This component gives the linear path to the particle.
Second is:
$v_{\perp}=v \: sin\theta$ i.e. Perpendicular to magnetic field $\overrightarrow{B}$. This component gives the circular path to the particle.
The resultant of these two-component gives the helical path to the particle whose axis is parallel to the magnetic field.
The radius of the circular path of the helix is
$r=\frac{mv_{\perp}}{qB}$
$r=\frac{mv \: sin\theta}{qB}$
The time period of the particle
$T=\frac{2\pi m}{qB}$
The linear distance traveled by the particle in the direction of the magnetic field in one complete circle is called the 'pitch $(p)$' of the path.
$p=v_{\parallel} \times T$
$T= v \: cos\theta \times \frac{2\pi m}{qB}$
Kinetic Energy of Charged Particle Moving in Uniform Magnetic Field→
The kinetic energy is
$K=\frac{1}{2}mv^{2}$
$K=\frac{(mv)^{2}}{2m}$
Now substitute the value of $mv$ from
$r=\frac{mv}{qB}$. Then we get
$K=\frac{1}{2}m \left( \frac{rqB}{m} \right)^{2}$
$K=\frac{r^{2}q^{2}B^{2}}{2m}$
$r$ → Radius of the circular path
$m$ → mass of the particle
 |
| The frequency and Time period of the particle are independent of the speed |
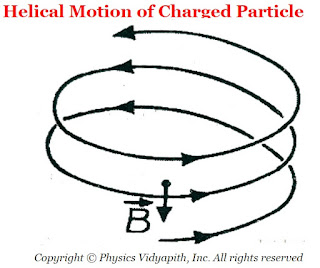 |
| Helical Motion of Charged Particle |
Normalized and Orthogonal wave function
Description:
We know that $\psi^{*}\psi$ or $\left|\psi \right|^{2} d\tau $ represent the probability of finding the particle in volume element $d\tau$.
The total probability of finding the particle in the entire space is 1 so
$ \int \left|\psi(r,t) \right|^{2} d\tau=1 $
Where integral extends overall space.
$\int \psi^{*}(r,t) \psi(r,t) d\tau=1$
A wave function satisfies the above equation so it is called normalized to unity.
For any wave function that is a solution of the time-dependent Schrodinger equation
$\int \psi^{*} \psi d\tau=N$
$\frac{1}{N} \int \psi^{*} \psi d\tau=1$
$\int \frac{\psi{*}}{\sqrt{N}} \frac{\psi}{\sqrt{N}} d\tau = 1$
Where
$\sqrt{N}$ → Normalized Factor
$\frac{\psi}{N} $ → Normalised wave function
If independent coordinate $x$,$y$,$z$, and $\psi$ satisfy the Schrodinger wave equation. Then it is evident that $\frac{\psi}{\sqrt {N}}$ also satisfies the Schrodinger wave equation.
If $\psi_{i}$ and $\psi_{j}$ are two different wave functions both the satisfactory solution of the wave equation for a given system. Then these functions will be normalized if
$\psi_{i}^{*} \psi_{i} d\tau=1 \quad and \quad \psi_{j}^{*} \psi_{j} d\tau=1$
If the two wave function $\psi_{i}$ and $\psi_{j}$ are the satisfactory solution of the wave equation for a given system. Then these functions will be mutually orthogonal if
$\psi_{i}^{*} \psi_{j} d\tau=0 \qquad Where \: $i \neq j$
$\psi_{j}^{*} \psi_{i} d\tau=0 \qquad Where \: $i \neq j$
These integral vanishes over the entire space.
$\sqrt{N}$ → Normalized Factor
$\frac{\psi}{N} $ → Normalised wave function
Quantum Mechanical Operators
Operator →
An operator is defined as a mathematical term that is used in the operation of a function so that this function may or may not be transformed into another function.
Operators of Quantum Mechanics →
There are the following quantum mechanical operators which are used in the wave function of particles:-
Momentum Operator
Kinetic Energy Operator
Total Energy Operator (Hamiltonian Operator)
Total Energy Operator in terms of the differential with respect to time
Momentum Operator →
The wave function for a free particle moving along the position $x$-direction is
$\psi(x,t)=A e^{\frac{i}{\hbar}(P_{x}x-Et)}$
Differentiate the above equation with respect to $x$ then we get
$\frac{\partial \psi}{\partial x}= A e^{\frac{i}{\hbar}(P_{x}x-Et)} \frac{i}{\hbar} P_{x} $
$\frac{\partial \psi}{\partial x}= \psi \frac{i}{\hbar} P_{x} $
$ P_{x} \psi = \frac{\hbar}{i}\frac{\partial \psi}{\partial x}$
$ P_{x} = \frac{\hbar}{i}\frac{\partial}{\partial x}$
For three dimensional:-
$\overrightarrow{P}= \frac{\hbar}{i} \overrightarrow{\nabla}$
Kinetic Energy Operator →
We know that the momentum operator
$ P_{x} \psi = \frac{\hbar}{i}\frac{\partial \psi}{\partial x} \qquad(1)$
Differentiate the above equation $(1)$ with respect to $x$ then we get
$ P_{x} \frac{\partial \psi}{\partial x} = \frac{\hbar}{i}\frac{\partial^{2} \psi}{\partial x^{2}} \qquad(2)$
Now substitute the value of $\frac{\partial \psi}{\partial x}$ from equation $(1)$ to equation $(2)$
$\frac{\hbar}{i}\frac{\partial^{2} \psi}{\partial x^{2}} = P_{x} \frac{i}{\hbar} P_{x} \psi$
$\frac{\hbar^{2}}{i^{2}}\frac{\partial^{2} \psi}{\partial x^{2}} = P_{x}^{2} \psi$
$ -\hbar^{2}\frac{\partial^{2} \psi}{\partial x^{2}} = P_{x}^{2} \psi \qquad (\because i^{2}=-1)$
$ -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \psi}{\partial x^{2}} = \frac{P_{x}^{2}}{2m} \psi \qquad {3}$
$ -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \psi}{\partial x^{2}} = K \psi \qquad (\because \frac{P_{x}^{2}}{2m} = K)$
$ K \psi = -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \psi}{\partial x^{2}} $
$ K = -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} $
For three dimensions:-
$ K = -\frac{\hbar^{2}}{2m}\nabla^{2} $
Total Energy Operator (Hamiltonian Operator) →
The total energy of the particle moving along $x4-aix is given by
$E=\frac{P_{x}^{2}}{2m} + V(x) \qquad(1)$
Where V(x) → Potential Energy
We know that the kinetic energy operator
$ K = -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} $
$ \frac{P_{x}^{2}}{2m} = -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} \qquad (\because K=\frac{P_{x}^{2}}{2m})$
Now substitute the value of $ \frac{P_{x}^{2}}{2m}$ in equation$(1)$
$E= -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} + V(x)$
Multiply $\psi$ on the both side of above equation
$E \psi= -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \psi }{\partial x^{2}} + V(x) \psi$
$E \psi= \left [ -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} + V(x) \right ] \psi$
$E \psi= \hat{H} \psi$
So the total energy operator
$ \hat{H} = \left [ -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} + V(x) \right ] $
For three dimensions:-
$\hat{H} = \left [ -\frac{\hbar^{2}}{2m}\nabla^{2} + V(x) \right ] $
The total energy operator is denoted by $\hat{H}$ and called the Hamiltonian Operator.
Total Energy Operator in terms of the differential with respect to time →
We know that the wave function
$\psi= A e^{\frac{i}{\hbar}}\left( P_{x}x - Et \right)$
Differentiate the above equation $(1)$ with respect to $t$ then we get
$\frac{\partial \psi}{\partial t}= A e^{\frac{i}{\hbar}(P_{x} x -Et)} \frac{i}{\hbar} (-E) $
$\frac{\partial \psi}{\partial t}= - \frac{i}{\hbar} E \psi $
$E \psi= -\frac{\hbar}{i} \frac{\partial \psi}{\partial t}$
$E \psi= i^{2} \frac{\hbar}{i} \frac{\partial \psi}{\partial t} \qquad (\because i^{2}=-1)$
$E \psi= i \hbar \frac{\partial \psi}{\partial t}$
This energy operator is denoted by $E$ so
$E = i \hbar \frac{\partial }{\partial t}$
Postulate of wave mechanics or Quantum Mechanics
Postulate of Wave or Quantum Mechanics (or Operator formalism in Quantum mechanics) →
The formulation of mathematical equations of quantum mechanics is based on the linear operator. This operator formulation of quantum mechanics is known as postulates of quantum mechanics. These postulates are given below:-
- For a system consisting of particles moving in a field of a conservative force, there is an associated complex wave function $\psi(x, y, z, t)$ where $x$,$y$,$z$ space coordinates, and $t$ is the time. This wave function enables us to obtain a description of the behavior of the system, consistent with the principle of uncertainty.
- There is an operator with every observable dynamical quantity. The operator corresponding to the pertinent dynamical quantities is:-
Dynamical Variable Symbol Quantum Mechanical Operator Position $x$
$y$
$z$$x$
$y$
$z$Momentum $P_{x}$
$P_{y}$
$P_{z}$
Generalised Form $\overrightarrow{P}$$\frac{\hbar}{i}\frac{\partial}{\partial x}$
$\frac{\hbar}{i}\frac{\partial}{\partial y}$
$\frac{\hbar}{i}\frac{\partial}{\partial z}$
Generalised Form $\frac{\hbar}{i}\overrightarrow{\nabla}$Total Energy $E$ $i\hbar \frac{\partial}{\partial t}$ Total Energy $E$ $-\frac{\hbar^{2}}{2m} \nabla^{2}+V(x)$
This is also known as Hamiltonian Operator $H$.Kinetic Energy $K$ $-\frac{\hbar^{2}}{2m} \nabla^{2}$ Potential Energy $V(x,y,z)$ $V(x,y,z)$ All the operators have eigen functions and eigen values. - The wave function $\psi(x,y,z,t)$ and its partial derivatives $\frac{\partial \psi}{\partial x}$, $\frac{\partial \psi}{\partial y}$, $\frac{\partial \psi}{\partial z}$ must be finite, continuous and single-valued for all values of $x$, $y$, $z$ and $t$
- The product of $\psi(x,y,z,t)$ and $\psi^{*}(x,y,z,t)$ is always a real quantity. The product is called the probability density and $\psi\psi^{*} d\tau $ is interpreted as a probability that the particle will be found in volume element $d\tau$ at $x$,$y$,$z$ and time $t$. Since the total probability of finding particles somewhere in the entire space must be equal to 1.
$\int_{-\infty}^{+\infty} \psi \: \psi^{*}\: d\tau = 1$The integral is taken overall space.
- The average or expectation value of an observable quantity $\alpha$ with which an operator $\hat{\alpha}$ is associated is defined by
$\left< \alpha \right> = \int_{-\infty}^{+\infty} \psi^{*} \hat{\alpha} \psi d\tau$
Eigenfunction, Eigenvalues and Eigenvectors
Eigenfunction and Eigenvalues →
If $\psi$ is a well-behaved function, then an operator $\hat{P}$ may operate on $\psi$ in two different ways depending upon the nature of function $\psi$ `
Eigenvalues and Eigenvectors →
Let a linear transformation equation
$AX=\lambda X \qquad(1)$
Where
A → Square matrix of $n$ order (where $n=1,2,3,.....$)
$\lambda$ → Scalar Factor
The equation $(1)$ may be written as
$AX=I\lambda X$
$AX-I\lambda X=0$
$(A-I\lambda)X=0 \qquad(2)$
Where $I$ is unit matrix
Any value of $\lambda$ for which equation $(1)$ or equation $(2)$ has non zero (i.e $X \neq 0$) solution is called eigenvalues or characteristic roots or latent root of the matrix $A$ and corresponding non zero solution of $X$ is called eigenvectors or characteristic vectors or latent vectors of the matrix $A$
The matrix $\left| A- \lambda I \right|$ is called characteristic matrix of $A$. The determinant $\phi(\lambda) = \left| A- \lambda I \right|$ is called the characteristic polynomial of $A$. So
$\phi(\lambda) = \left| A- \lambda I \right| =0$
And $\phi(x)= a_{0}+a_{1} \lambda a_{2} \lambda^{2}+ .......+a_{n} \lambda^{n}=0 $
- When an operator $\hat{P}$ operates on any function $\psi$ then this function $\psi$ changes into another function $\phi$. i.e.
$\hat{P} \psi =\phi$Where $\phi$ is a new function linearly depending upon the initial function $\psi$.Example:Let us consider a function $f(x)=x^{2}$ and an operator ie. differential operator $\frac{d}{dx}$ is operate on the function. Then we get$\frac{d}{dx}f(x)= \frac{d}{dx} (x^{2})$$\frac{d}{dx}f(x)= 2x$Now the given function $f(x)=x^{2}$ change into another function $f(x)=x$.
-
When an operator $\hat{P}$ operates on any function $\psi$ then this function $\psi$ does not change into another function but now this function $\psi$ may be with multiples of complex or real numbers(or values).i.e
$\hat{P} \psi =\lambda \phi$Where $\lambda$ is Real OR Complex Number. This number or value is known as Eigenvalues.In this case, the function $\psi$ is a member of the class of physically meaningful functions called the eigen function of the operator $\hat{P}$. The number $\lambda$ is called the eigen value of operator $\hat{P}$ associated with eigen function $\psi$ and this equation is known as the eigenvalue equation.Example: Let us consider a function $f(x)=e^{2x}$ and an operator ie. differential operator $\frac{d}{dx}$ is operate on the function. Then we get$\frac{d}{dx}f(x)= \frac{d}{dx} (e^{2x})$$\frac{d}{dx}f(x)= 2e^{2x}$Now the given function $f(x)=e^{2x}$ change into another function $f(x)=x$.
A → Square matrix of $n$ order (where $n=1,2,3,.....$)
$\lambda$ → Scalar Factor
Kepler's Laws of Planetary Motion
Kepler's Laws →
Kepler's found important uniformity in the motion of the planets. This uniformity is known as "Kepler's Laws of planetary motion".
There are basically three laws →
First law (Law of orbits) →
Second Law (Law of Areal Speed) →
According to the second law, When the planet is farthest from the sun, then its speed is maximum, and when it is nearest the sun, then its speed is maximum.
From the above figure, A planet is moving around the sun from $A$ to $B$ in a given time interval, and from $C$ to $D$ in the same time interval, then according to the law of areal speed, the areas $ASB$ and $CSD$ will be equal with respect to the same time-interval
Proof →
Let us consider, A planet moves the angle $d\theta$ from $A$ to $B$ in the infinitesimal interval of time $dt$, then the area swept out by radial line $SA$ is
$dA$= Area of the curved $\Delta$ $SAB$
$dA \approx \frac{1}{2} \left( AB \times SA \right)$
$dA \approx \frac{1}{2} \left( r \: d\theta \times r \right)$
$dA \approx \frac{1}{2} \left( r^{2} \: d\theta \right)$
Thus, the instantaneous areal speed of the planets is
$\frac{dA}{dt}=\frac{1}{2} r^{2} \frac{d \theta}{dt}$
$\frac{dA}{dt}=\frac{1}{2} r^{2} \omega \qquad(1)$
Where $\omega$ → The angular speed of the planet.
We know that
$J=I \: \omega$
Where $I$ is the instantaneous moment of inertia of the planet about the Sun $S$.
$J=m \: r^{2} \: \omega \qquad(2)$
Where $m$ is the mass of the planet. Now substitute the value of $r^{2} \: \omega$ from equation $(2)$ in equation $(1)$.
$\frac{dA}{dt}=\frac{J}{2m} \left( Constant \right)$
From the above equation, The areal speed $\frac{dA}{dt}$ of the planet is constant which is Kepler's Second Law. The above equation shows that the angular momentum of the planet is constant. i.e. The angular momentum of any planet is conserved.
Third Law (Law of Periods) →
Proof →
Let $a$ and $b$ be the semi-major and semi-minor axes of the ellipse, then the area of the ellipse will be $\pi ab$. Let $T$ is the period of one complete revolution of any planet, then
$T=\frac{Area \: of \: the \: ellipse}{Areal \: Speed}$
$T=\frac{\pi a b}{\frac{J}{2m}}$
$T=\frac{2\pi a b m}{J}$
$T^{2}=\frac{4 \pi^{2} a^{2} b^{2} m^{2}}{J^{2}}$
Let $l$ be the semi-latus rectum of the elliptical orbit i.e. $l=\frac{b^{2}}{a}$. Then we get the above equation which can be written as
$T^{2}=\frac{4 \pi^{2} m^{2} a^{3} l }{J^{2}}$
$T^{2} \propto a^{3} $
Where $\frac{4 \pi^{2} m^{2} l }{J^{2}}$ is constant.
From the above equation, It is clear that the larger the distance of a planet from the sun, the larger will be its period of revolution around the sun. The period of revolution of the nearest planet to the sun i.e. Mercury is $88$ days, while that of the faraway planet from the sun i.e. Pluto is $248$ years.
- First law (Law of orbits)
- Second Law (Law of Areal Speed)
- Third Law (Law of Periods)
All the planets move around the sun in elliptical path and the sun is at the one foci of the ellipse.
A line joining the any planet to sun sweeps out equal areas in equal interval of of times. i.e The areal speed of the planets remains constant.
 |
| Planetary Motion |
The square of the time period of one complete revolution of any planet around the sun is directly proportional to the cube of the semi-major axis of its elliptical orbit.
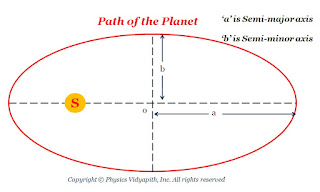 |
| Path of the Planet |
Relation between gravitational acceleration and gravitational force
Relation between $g$ and $G$ →
Let us consider:
The mass of earth = $M_{e}$
The radius of earth = $R_{e}$
The mass of the object = $m$
If the object is placed on the surface of the earth then the gravitational force on the object is →
$F=G \frac{M_{e} m}{R_{e}^{2}} \qquad(1)$
The force on the object due to gravitational acceleration is →
$F=mg \qquad(2)$
From equation $(1)$ and equation $(2)$
$mg=G \frac{M_{e} m}{R_{e}^{2}}$
$g=G \frac{M_{e}}{R_{e}^{2}}$
$G M_{e}=g R_{e}^{2}$
The mass of earth = $M_{e}$
The radius of earth = $R_{e}$
The mass of the object = $m$
Newton's law for Gravitational Force
Gravitational Force →
Newton's Gravitational Law statement is a combination of three individual statements. These are
$F\propto \frac{m_{1} \: m_{2}}{r^{2}}$
$F=G \frac{m_{1} \: m_{2}}{r^{2}}$
Where $G$ is Newton's gravitaional constant and its experimental value $6.67\times 10^{-11} \frac{N-m^{2}}{kg^{2}}$
Properties of Newton's law for Gravitational force →
There are the following properties of Newton's law for gravitational force
Gravitational force is always an attractive force.
Gravitational force is action and reaction pair and follows Newton's third law.
A Gravitational force is a conservative force.
Gravitational force is central force i.e. it is always acting along the line joining between two particles.
Unit and Dimensional formula of $G$
The unit of $G$ is $\frac{N-m^{2}}{kg^{2}}$
The dimensional Formula of $G$ is $[M^{-1}L^{3}T^{-2}]$
- The force between the two-particle is directly proportional to the product of their masses i.e.
$F \propto m_{1} \: m_{2} \qquad(1)$Where $m_{1}$ & $m_{2}$ are the masses of the particles. - The force between the two-particle is inversely proportional to the square of the distance between them i.e.
$F \propto \frac{1}{r^{2}} \qquad(2)$Where $r$ is the distance between the particles. - This force always acts between the line joining the masses.
Popular Posts
-
Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is ...
-
Angle of Acceptance → "If incident angle of light on the core for which the incident angle on the core-cladding interface equals t...
-
Derivation of interference of light due to a wedge-shaped thin film: Interference of light due to wedge-shaped thin film The wedge...
-
Maxwell's Equations: Maxwell's equation of the electromagnetic wave is a collection of four equations i.e. Gauss's law of elec...
-
Let a plane wavefront be incident normally on slit $S_{1}$ and $S_{2}$ of equal $e$ and separated by an opaque distance $d$.The diffracted l...
Study-Material
Categories
Alternating Current Circuits
(10)
Atomic and Molecular Physics
(4)
Biomedical
(1)
Capacitors
(6)
Classical Mechanics
(12)
Current carrying loop in magnetic field
(5)
Current Electricity
(10)
Dielectric Materials
(1)
Electromagnetic Induction
(3)
Electromagnetic Wave Theory
(23)
Electrostatic
(22)
Energy Science and Engineering
(2)
Error and Measurement
(2)
Gravitation
(11)
Heat and Thermodynamics
(3)
Kinematics Theory Of Gases
(2)
Laser System & Application
(15)
Magnetic Effect of Current
(9)
Magnetic Substances
(3)
Mechanical Properties of Fluids
(5)
Nanoscience & Nanotechnology
(4)
Nuclear Physics
(7)
Numerical Problems and Solutions
(2)
Optical Fibre
(5)
Optics
(25)
Photoelectric Effect
(3)
Quantum Mechanics
(37)
Relativity
(8)
Semiconductors
(2)
Superconductors
(1)
Topic wise MCQ
(9)
Units and Dimensions
(1)
Waves
(5)