Physical Significance:
The physical significance of Maxwell's equations obtained from integral form are given below:
Maxwell's First Equation:
1. The total electric displacement through the surface enclosing a volume is equal to the total charge within the volume.
2. It represents Gauss Law.
3. This law is independent of time.
Charge acts as source or sink for the lines of electric force.
Maxwell's Second Equation:
1. The total magnetic flux emitting through any closed surface is zero. An isolated magnet do not exist monopoles.
2. There is no source or sink for lines of magnetic force.
3. This is time independent equation.
Maxwell's Third Equation:
1. The electromotive force around the closed path is equal to the time derivative of the magnetic displacement through any surface bounded by the path.
2. This gives relation between electric field $E$ and magnetic induction $B$.
3. This expression is time varying i.e. $E$ is generated by time variation of $B$.
4.This gives relation in variation of E with the time variation of $B$ or $H$.
5. This is a mathematical form of Faraday's law of electromagnetic induction or Lenz's
Law.
Maxwell's Fourth Equation:
1. The magneto-motive force around the closed path is equal to the conduction current
plus displacement current through any surface bounded by the path.
2. This is time dependent wave equation.
3 This is a mathematical form of Ampere circuital law.
4. Magnetic induction $B$ can be generated from $J$ and time variation of magnetic displacement $D$.
5. This relates the space variation of $B$ with time variation of $D$.
Circuit containing Inductor and Capacitor in Series (L-C Series Circuit )
Mathematical Analysis of L-C Series Circuit :
Let us consider, a circuit containing inductor $L$ capacitor $C$ and these are connected in series. If an alternating voltage source is applied across it then the resultant voltage of the L-C circuit
$V=V_{L} - V_{C} \qquad(1)$
We know that:
$V_{L} = iX_{L}$
$V_{C} = iX_{C}$
So from equation $(1)$
$V= iX_{L} - iX_{C} $
$V=i \left(X_{L} - X_{C} \right) $
$\frac{V}{i}=\left(X_{L} - X_{C} \right) $
$Z=\left(X_{L} - X_{C} \right) \qquad(2)$
Where
$Z \rightarrow$ Impedance of L-C circuit.
$X_{L} \rightarrow$ Inductive Reactance which has value $\omega L$
$X_{C} \rightarrow$ Capacitive Reactance which has value $\frac{1}{\omega C}$
So from equation $(2)$, we get
$Z=\left( \omega L - \frac{1}{\omega C} \right) \qquad(3)$
The phase of resultant voltage:
The phase of resultant voltage from current is $90^{\circ}$ as shown in the figure above.
The Impedance and Phase at Resonance Condition:($X_{L} = X_{C}$):
At resonance $X_{L} = X_{C} \qquad(5)$
$\omega L = \frac{1}{\omega C}$
$\omega^{2} = \frac{1}{L C}$
$\omega = \sqrt{\frac{1}{L C}}$
$2 \pi f = \sqrt{\frac{1}{L C}}$
$ f = \frac{1}{2 \pi}\sqrt{\frac{1}{L C}}$
Where $f \rightarrow$ Natural frequency of the circuit.
1.) The Impedance of the circuit at resonance condition:
Substitute the resonance condition i.e. $X_{L} = X_{C}$ in equation $(2)$ then the impedance of the L-C Circuit
$Z=0$
The impedance of the L-C circuit at resonance condition is zero.
2.) The Phase of resultant voltage at resonance condition:
There is not any change in the phase of resultant voltage at resonance condition i.e. that will be the same $90^{\circ}$.
$V_{C} = iX_{C}$
$Z \rightarrow$ Impedance of L-C circuit.
$X_{L} \rightarrow$ Inductive Reactance which has value $\omega L$
$X_{C} \rightarrow$ Capacitive Reactance which has value $\frac{1}{\omega C}$
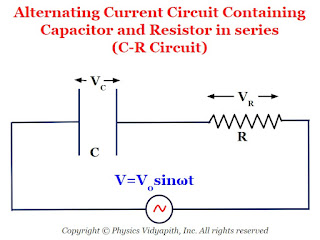
Circuit containing Capacitor and Resistor in Series (C-R Series Circuit )
Mathematical Analysis of C-R Series Circuit :
Let us consider, a circuit containing capacitor $C$ resistor $R$ and these are connected in series. If an alternating voltage source is applied across it then the resultant voltage of the C-R circuit
$V=\sqrt{ V_{C} ^{2} + V^{2}_{R}} \qquad(1)$
We know that:
$V_{R} = iR$
$V_{C} = iX_{C}$
So from equation $(1)$
$V=\sqrt{\left( iX_{C} \right)^{2} + \left(iR\right)^{2}} $
$V=i\sqrt{\left( X_{C} \right)^{2} + R^{2}} $
$\frac{V}{i}=\sqrt{\left( X_{C} \right)^{2} + R^{2}} $
$Z=\sqrt{\left( X_{C} \right)^{2} + R^{2}} \qquad(2)$
Where
$Z \rightarrow$ Impedance of C-R circuit.
$X_{C} \rightarrow$ Capacitive Reactance which has value $\frac{1}{\omega C}$
So from equation $(2)$, we get
$Z=\sqrt{\left( \frac{1}{\omega C} \right)^{2} + R^{2}} \qquad(3)$
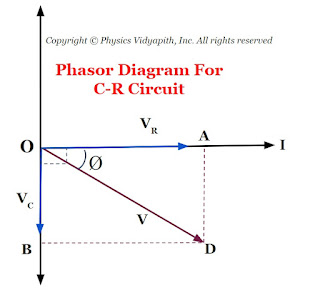
The phase of resultant voltage:
If the phase of resultant voltage from from current is $\phi$ then
$tan \phi = \frac{X_{C} }{R} \qquad(4)$
$tan \phi = \frac{\frac{1}{\omega C}}{R} $
$tan \phi = \frac{1}{\omega C R} $
$\phi = tan^{1} \left(\frac{1}{\omega C R}\right) $
$V_{C} = iX_{C}$
$Z \rightarrow$ Impedance of C-R circuit.
$X_{C} \rightarrow$ Capacitive Reactance which has value $\frac{1}{\omega C}$
Circuit containing Inductor and Resistor in Series (L-R Series Circuit )
Mathematical Analysis of L-R Series Circuit :
Let us consider, a circuit containing inductor $L$ resistor $R$ and these are connected in series. If an alternating voltage source is applied across it then the resultant voltage of the L-R circuit
$V=\sqrt{ V_{L} ^{2} + V^{2}_{R}} \qquad(1)$
We know that:
$V_{R} = iR$
$V_{L} = iX_{L}$
So from equation $(1)$
$V=\sqrt{\left( iX_{L} \right)^{2} + \left(iR\right)^{2}} $
$V=i\sqrt{\left( X_{L} \right)^{2} + R^{2}} $
$\frac{V}{i}=\sqrt{\left( X_{L} \right)^{2} + R^{2}} $
$Z=\sqrt{\left( X_{L} \right)^{2} + R^{2}} \qquad(2)$
Where
$Z \rightarrow$ Impedance of L-R circuit.
$X_{L} \rightarrow$ Inductive Reactance which has value $\omega L$
So from equation $(2)$, we get
$Z=\sqrt{\left( \omega L \right)^{2} + R^{2}} \qquad(3)$
The phase of resultant voltage:
If the phase of resultant voltage from from current is $\phi$ then
$tan \phi = \frac{X_{L} }{R} \qquad(4)$
$tan \phi = \frac{\omega L }{R} $
$\phi = tan^{1} \left(\frac{\omega L }{R}\right) $
$V_{L} = iX_{L}$
$Z \rightarrow$ Impedance of L-R circuit.
$X_{L} \rightarrow$ Inductive Reactance which has value $\omega L$
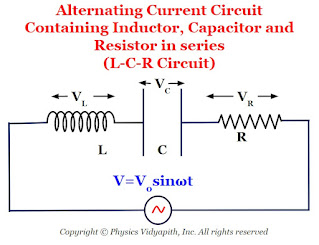
Circuit containing Inductor, Capacitor, and Resistor in Series (L-C-R Series Circuit )
Mathematical Analysis of L-C-R Series Circuit :
Let us consider, a circuit containing inductor $L$, capacitor $C$, and resistor $R$ and these are connected in series. If an alternating voltage source is applied across it then the resultant voltage of the L-C-R circuit
$V=\sqrt{\left( V_{L} -V_{C} \right)^{2} + V^{2}_{R}} \qquad(1)$
We know that:
$V_{R} = iR$
$V_{L} = iX_{L}$
$V_{C} = iX_{C}$
So from equation $(1)$
$V=\sqrt{\left( iX_{L} - iX_{C} \right)^{2} + (iR)^{2}} $
$V=i\sqrt{\left( X_{L} - X_{C} \right)^{2} + R^{2}} $
$\frac{V}{i}=\sqrt{\left( X_{L} - X_{C} \right)^{2} + R^{2}} $
$Z=\sqrt{\left( X_{L} - X_{C} \right)^{2} + R^{2}} \qquad(2)$
Where
$Z \rightarrow$ Impedance of L-C-R circuit.
$X_{L} \rightarrow$ Inductive Reactance which has value $\omega L$
$X_{C} \rightarrow$ Inductive Reactance which has value $\frac{1}{\omega C}$
So from equation $(2)$, we get
$Z=\sqrt{\left( \omega L - \frac{1}{\omega C} \right)^{2} + R^{2}} \qquad(3)$
The phase of resultant voltage:
If the phase of resultant voltage from from current is $\phi$ then
$tan \phi = \frac{X_{L} - X_{C}}{R} \qquad(4)$
$tan \phi = \frac{\omega L - \frac{1}{\omega C}}{R} $
$ \phi = tan^{-1} \left( \frac{\omega L - \frac{1}{\omega C}}{R} \right) $
The Impedance and Phase at Resonance Condition:($X_{L} = X_{C}$):
At resonance $X_{L} = X_{C} \qquad(5)$
$\omega L = \frac{1}{\omega C}$
$\omega^{2} = \frac{1}{L C}$
$\omega = \sqrt{\frac{1}{L C}}$
$2 \pi f = \sqrt{\frac{1}{L C}}$
$ f = \frac{1}{2 \pi}\sqrt{\frac{1}{L C}}$
Where $f \rightarrow$ Natural frequency of the circuit
1.) The Impedance of the circuit at resonance condition:
Substitute the resonance condition i.e. $X_{L} = X_{C}$ in equation $(2)$ then the impedance of the L-C-R Circuit
$Z=R$
The impedance of the L-C-R circuit at resonance condition is equal to the resistance of the resistor applied in a circuit.
2.) The Phase of resultant voltage at resonance condition:
$tan\phi =0$
$tan\phi = tan 0^{\circ}$
$\phi=0^{\circ}$
The phase of resultant voltage at resonance condition is zero. i.e. the direction of resultant voltage in the direction of current in the circuit.
Note: There are following cases arise in the L-C-R circuit at resonance condition
Case -1:
If $X_{L} \gt X_{C}$, the $tan \phi$ is positive, i.e. $\phi$ is positive. In this case, the voltage leads to the current. Therefore, the circuit is more inductive rather than capacitive or resistive.
Case -2:
If $X_{L} \lt X_{C}$, the $tan \phi$ is negative, i.e. $\phi$ is negative. In this case, the voltage lags behind the current. Therefore, the circuit has a more capacitance-dominated circuit.
Case -3:
If $X_{L} = X_{C}$, the $tan \phi$ is zero, i.e. $\phi$ is negative. In this case, the voltage and the current are in phase. Therefore, the circuit is purely resistive.
$V_{L} = iX_{L}$
$V_{C} = iX_{C}$
$Z \rightarrow$ Impedance of L-C-R circuit.
$X_{L} \rightarrow$ Inductive Reactance which has value $\omega L$
$X_{C} \rightarrow$ Inductive Reactance which has value $\frac{1}{\omega C}$
Merits and Demerits of Alternating Current in Comparison to Direct Current
Merits and Demerits of AC in Comparison to DC
(a) Merits
(i) Alternating current can be increased or decreased by using a transformer.
This is the reason that Alternating current can be transmitted from one place to other place at relatively lower expenditure and minimum loss of energy. In Direct current, it is not possible.
(ii) Alternating current can be controlled by choke coil or capacitor at very small loss of energy. To control Direct current resistance is required in which energy loss is very high.
(ii) Alternating current can easily be converted into Direct current by using a rectifier but converting Direct current into Alternating current is not easy.
(iv) Alternating current is cheaper than DC. (life of a cell or battery is very limited).
(b) Demerits
(i) Alternating current is more dangerous as compared to Direct current.
(ii) Alternating current cannot be used in electrolysis.
(iii) Most of the Alternating current of high frequency flows on the surface of the wire, therefore, a thick wire by joining number of thin insulated wires in parallel are to be used.
Power in Alternating Current Circuit
Definition of Power in Alternating Current Circuit:
The rate of power consumption in an alternating current circuit is known as power in the circuit.
Mathematical Analysis:
Let us consider an alternating current circuit in which the voltage and current at any instant are given by
$V=V_{\circ} sin \omega t \qquad(1)$
$i=i_{\circ} sin \left( \omega t - \phi \right) \qquad(2)$
Where $\phi$ $\rightarrow$ Phase difference between voltage and current
So instantaneous Power
$P=Vi$
$P=\left\{V_{\circ} sin \omega t \right\} \left\{ i_{\circ} sin \left( \omega t - \phi \right) \right\}$
$P=V_{\circ} i_{\circ} \: sin \omega t \: sin \left( \omega t - \phi \right)$
$P=\frac{V_{\circ} i_{\circ}}{2} \left[2\: sin \: \omega t \: sin \left( \omega t - \phi \right)\right]$
$P=\frac{V_{\circ} i_{\circ}}{2} \left[ cos \left( \omega t -\omega t + \phi \right) \\ \qquad - cos \left( \omega t + \omega t - \phi \right) \right]$
$P=\frac{V_{\circ} i_{\circ}}{2} \left[ cos \left(\phi \right) - cos \left( 2\omega t - \phi \right) \right]$
The average power for one cycle is:
$P_{avg}$ = The average value of $\left\{ \frac{V_{\circ} i_{\circ}}{2} \left[ cos \left(\phi \right) - cos \left( 2\omega t - \phi \right) \right] \right\}$
The term $cos \left( 2\omega t - \phi \right)$ is time-dependent and the average value of term $cos \left( 2\omega t - \phi \right)$ for complete one cycle is zero. So the average power dissipation in one cycle is
$P_{avg}= \frac{V_{\circ} i_{\circ}}{2} cos \phi $
$P_{avg}= \frac{V_{\circ}}{\sqrt{2}} \frac{i_{\circ}}{\sqrt{2}} cos \phi $
$P_{avg}= V_{rms} \: i_{rms} cos \phi $
Case -1 The circuit containing Pure Resistor only:
If the circuit contains a pure resistance only then voltage $V$ and current $i$ are always in the same phase. i.e. $\phi=0^{\circ}$ and $cos \phi = +1$, then average power
$P_{avg}= V_{rms} \: i_{rms} $
Case -2 The circuit containing Pure Inductor only:
If the circuit containing pure inductor only then voltage $V$ leads over current $i$ by $90^{\circ}$ i.e. $\phi=90^{\circ}$ and $cos 90^{\circ} = 0$, then average power
$P_{avg}= 0 $
Case -3 The circuit containing Pure Capacitor only:
If the circuit containing pure capacitor only then voltage $V$ lags behind current $i$ by $90^{\circ}$ i.e. $\phi=90^{\circ}$ and $cos 90^{\circ} = 0$, then average power
$P_{avg}= 0 $
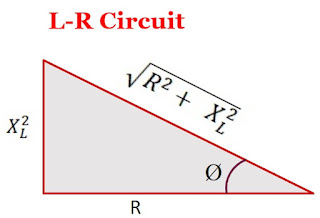
Case -4 The circuit containing inductor and resistor only (L-R Circuit):
We know that the phase in the L-R circuit is
$tan \phi = \frac{X_{L}}{R}$
From the above equation, Draw the triangle as shown in the figure below:
From the above figure, the value of $cos\phi$ is
$cos \phi = \frac{R}{\sqrt{R^{2} + X^{2}_{L}}}$
So average power
$P_{avg}= V_{rms} \: i_{rms} \frac{R}{\sqrt{R^{2} + X^{2}_{L}}} $
$\left(P_{avg}\right)_{L-R} \lt \left(P_{avg}\right)_{R}$
Thus, the average power consumption in an L-R circuit is less than the power consumed in a purely resistive circuit
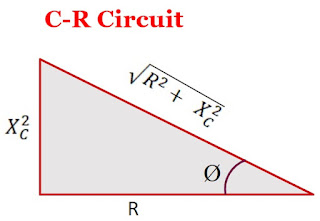
Case -5 The circuit containing capacitor and resistor only (C-R Circuit):
We know that the phase in the C-R circuit is
$tan \phi = \frac{X_{C}}{R}$
From the above equation, Draw the triangle as shown in the figure below:
From the above figure, the value of $cos\phi$ is
$cos \phi = \frac{R}{\sqrt{R^{2} + X^{2}_{C}}}$
So average power
$P_{avg}= V_{rms} \: i_{rms} \frac{R}{\sqrt{R^{2} + X^{2}_{C}}} $
$\left(P_{avg}\right)_{C-R} \lt \left(P_{avg}\right)_{R}$
Thus, the average power consumption in a C-R circuit is less than the power consumed in a purely resistive circuit
Case -6 The circuit containing capacitor and inductor only (L-C Circuit):
We know that the phase in the L-R circuit is
$\phi = 90^{\circ}$ and $cos 90^{\circ} = 0$
So average power
$P_{avg}= 0 $
Case -7 The circuit containing inductor, capacitor, and resistor only (L-C-R Circuit):
We know that the phase in the L-C-R circuit is
$tan \phi = \frac{X_{L} - X_{C}}{R}$
From the above equation, Draw the triangle as shown in the figure below:
From the above figure, the value of $cos\phi$ is
$cos \phi = \frac{R^{2}}{\sqrt{R^{2} + \left( X^{2}_{L} - X^{2}_{C} \right) }}$
So average power
$P_{avg}= V_{rms} \: i_{rms} \frac{R^{2}}{\sqrt{R^{2} + \left( X^{2}_{L} - X^{2}_{C} \right) }} $
$\left(P_{avg}\right)_{L-C-R} \lt \left(P_{avg}\right)_{R}$
Thus, the average power consumption in an L-C-R circuit is less than the power consumed in a purely resistive circuit
Wattless Current:
If the circuit contains only resistor or only inductor or only inductor and capacitor then power consumption in the circuit will be zero (i.e. there will be no energy dissipation in the circuit) due to the phase difference $90^{\circ}$ between voltage(or impedance) and current. So the current in the circuit is called the "Wattless current".
Self Induction Phenomenon and its Coefficient
Self Induction:
When a changing current flows in a coil then due to the change in magnetic flux in the coil produces an electro-motive force $\left(emf \right)$ in that coil. This phenomenon is called the principle of Self Induction.
The direction of electro-motive force can be found by applying "Lenz's Law".
Mathematical Analysis of Coefficient of Self Induction:
Let us consider that a coil having the number of turns is $N$. If the change in current is $i$, then linkage flux in a coil will be
$N \phi \propto i$
$N\phi = L i \qquad(1)$
Where $L$ $\rightarrow$ Coefficient of Self Induction.
According to Faraday's law of electromagnetic induction. The electro-motive force $\left(emf \right)$ in a coil is
$e=-N\left( \frac{d \phi}{dt} \right)$
$e=-\frac{d \left(N \phi \right)}{dt} \qquad(2)$
From equation $(1)$ and equation $(2)$
$e=-\frac{d \left(L i\right)}{dt} $
$e=-L \left(\frac{d i}{dt} \right) $
$L = \frac{e}{\left(\frac{d i}{dt} \right)}$
If $\left(\frac{d i}{dt} \right) = 1$
Then
$L = e$
The above equation shows that If the rate of flow of current in a coil is unit then the coefficient of self-induction in that coil will be equal to the induced electro-motive force $\left( emf \right)$.
Mutual Induction Phenomenon and its Coefficient
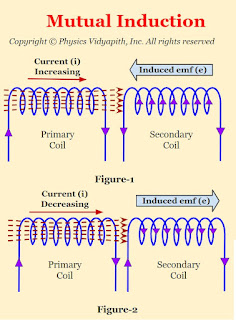
Mutual Induction:
When two coils are placed near each other then the change in current in one coil ( Primary Coil) produces electro-motive force $\left( emf \right)$ in the adjacent coil ( i.e. secondary coil). This phenomenon is called the principle of Mutual Induction.
The direction of electro-motive force $\left( emf \right)$ depends or can be found by "Lenz's Law"
Mathematical Analysis of Coefficient of Mutual Induction:
Let us consider that two coils having the number of turns are $N_{1}$ and $N_{2}$. If these coils are placed near to each other and the change in current of the primary coil is $i_{1}$, then linkage flux in the secondary coil will be
$N_{2}\phi_{2} \propto i_{1}$
$N_{2}\phi_{2} = M i_{1} \qquad(1)$
Where $M$ $\rightarrow$ Coefficient of Mutual Induction.
According to Faraday's law of electromagnetic induction. The electro-motive force $\left( emf \right)$ in the secondary coil is
$e_{2}=-N_{2}\left( \frac{d \phi_{2}}{dt} \right)$
$e_{2}=-\frac{d \left(N_{2} \phi_{2} \right)}{dt} \qquad(2)$
From equation $(1)$ and equation $(2)$
$e_{2}=-\frac{d \left(M i_{1} \right)}{dt} $
$e_{2}=-M \left(\frac{d i_{1}}{dt} \right) $
$M = \frac{e_{2}}{\left(\frac{d i_{1}}{dt} \right)}$
If $\left(\frac{d i_{1}}{dt} \right) = 1$
Then
$M = e_{2}$
The above equation shows that If the rate of flow of current in the primary coil is unit then the coefficient of mutual induction will be equal to the induced electro-motive force $\left( emf \right)$ in the secondary coil.
Faraday's laws of electromagnetic induction
Faraday's Laws of Electromagnetic Induction:
The Faraday's experiment shows the two laws which are known as Farday's laws of electromagnetic induction
First Law (Neumann's Law): The rate of change of magnetic flux through a circuit is equal to the emf produced in the circuit. This is also known as "Neumann Law"
$e=-\frac{\Delta \phi}{ \Delta t}$
Here negative sign shows the direction of emf.
If $\Delta t \rightarrow 0$
$e=-\frac{d \phi}{ d t}$
This equation represents an independent experimental law that cannot be derived from other experimental laws.
If the circuit is a tightly wound coil of $N$ turns, then the induced emf
$e=-N\frac{d \phi}{ d t}$
$e=-\frac{d \left(N \phi\right)}{ dt}$
Here $N \phi$ is called the 'Linkage magnetic flux'.
Note: The change in flux induces emf, not the current.
Second Law (Lenz's Law): The direction of induced EMF produced in a closed circuit is such that it opposes the original cause that produces it. It is also called "Lenz's law". The direction of induced EMF is described by Fleming's right-hand rule.
Paramagnetic Substances and Its properties
Paramagnetic Substances :
Those substances, which are placed in the external magnetic field and they are weakly magnetized in the direction of the external magnetic field, are called paramagnetic substances.
The susceptibility $\chi_{m} $ of paramagnetic substances is small and positive. Further, When a paramagnetic substance is placed in the magnetic field, then the flux density of the paramagnetic substance is slightly more than the free space. Thus, the relative permeability of paramagnetic substance $\mu_{r}$, is slightly more than 1.
Properties of Paramagnetic substances:
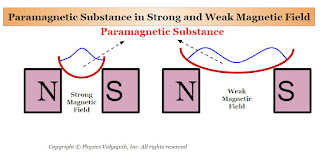
1. When a rod of a paramagnetic material is suspended freely between external magnetic poles (i.e. Between North and South Poles) then its axis becomes along the direction of the external magnetic field $B$ (Figure). The poles produced on the two sides of the rod are opposite to the poles of the external magnetic field.
2. In a non-uniform magnetic field, a paramagnetic substance tends to move from the weaker magnetic field to the stronger magnetic field. If a paramagnetic liquid is taken in a watch glass placed on two magnetic poles very near to each other, then the liquid rises in the middle as shown in the figure below(Figure) where the field is strongest. Now, if the distance between the poles is increased, the liquid is depressed in the middle, because now the field is strongest near the poles.
3. If the solution of a paramagnetic substance is poured into a U-tube and apply the strong magnetic field into one arm of this U-tube then the level of the solution in that arm rises. As shown in the figure below:
4. When paramagnetic gas molecules are passed between the poles of a magnet then paramagnetic gas molecules are attracted toward the magnetic field.
5. The susceptibility of a paramagnetic substance is inversely dependent on temperature.
$\chi \propto \frac{1}{T_{C}-T}$
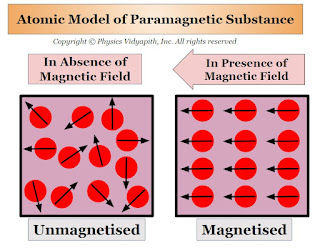
Explanation of Paramagnetism on the Basis of Atomic Model:
The property of Paramagnetism is generally found in those substances whose atoms (or ions or molecules) have an 'odd' number of electrons. In these odd numbers of electrons one electron is not able to form a pair because the net magnetic dipole moment of the atoms (or ions or molecules) are not zero. but in the absence of an external magnetic field, these magnetic dipole moments are randomly arranged inside the substance because the net magnetic dipole moment of the material is zero.
When a paramagnetic substance is placed in an external magnetic field $B$ then the magnetic dipole moment of the atoms (or ions or molecules) are weakly aligned in the direction of the external magnetic field. Thus, a small magnetic dipole moment is induced in the substance which is directly proportional to the magnetic field $B$. Hence, the paramagnetic substance is magnetized in the direction of the external magnetic field $B$, and the field lines become less dense inside the paramagnetic substance compared to those outside.
Popular Posts
-
Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is ...
-
Angle of Acceptance → "If incident angle of light on the core for which the incident angle on the core-cladding interface equals t...
-
Derivation of interference of light due to a wedge-shaped thin film: Interference of light due to wedge-shaped thin film The wedge...
-
Maxwell's Equations: Maxwell's equation of the electromagnetic wave is a collection of four equations i.e. Gauss's law of elec...
-
Let a plane wavefront be incident normally on slit $S_{1}$ and $S_{2}$ of equal $e$ and separated by an opaque distance $d$.The diffracted l...
Study-Material
Categories
Alternating Current Circuits
(10)
Atomic and Molecular Physics
(4)
Biomedical
(1)
Capacitors
(6)
Classical Mechanics
(12)
Current carrying loop in magnetic field
(5)
Current Electricity
(10)
Dielectric Materials
(1)
Electromagnetic Induction
(3)
Electromagnetic Wave Theory
(23)
Electrostatic
(22)
Energy Science and Engineering
(2)
Error and Measurement
(2)
Gravitation
(11)
Heat and Thermodynamics
(3)
Kinematics Theory Of Gases
(2)
Laser System & Application
(15)
Magnetic Effect of Current
(9)
Magnetic Substances
(3)
Mechanical Properties of Fluids
(4)
Nanoscience & Nanotechnology
(4)
Nuclear Physics
(7)
Numerical Problems and Solutions
(2)
Optical Fibre
(5)
Optics
(25)
Photoelectric Effect
(3)
Quantum Mechanics
(34)
Relativity
(8)
Semiconductors
(2)
Superconductors
(1)
Topic wise MCQ
(9)
Units and Dimensions
(1)
Waves
(5)