Equation of eigen value of the momentum of a particle in one dimension box:
The eigen value of the momentum $P_{n}$ of a particle in one dimension box moving along the x-axis is given by
$P^{2}_{n} = 2 m E_{n}$
$P^{2}_{n} = 2 m \frac{n^{2} \pi^{2} \hbar^{2}}{2 m L^{2}} \qquad \left( \because E_{n}= \frac{n^{2} \pi^{2} \hbar^{2}}{2 m L^{2}} \right)$
$P^{2}_{n} = \frac{n^{2} \pi^{2} \hbar^{2}}{L^{2}}$
$P_{n} = \pm \frac{n \pi \hbar}{L}$
$P_{n} = \pm \frac{n h}{2L} \qquad \left( \hbar = \frac{h}{2 \pi} \right)$
The $\pm$ sign indicates that the particle is moving back and forth in the infinite potential box.
The above equation shows that eigen value of the momentum of the particle is discrete and the difference between the momentum corresponding to two consecutive energy levels is always constant and equal to $\frac{h}{2L}$
Showing posts with label Quantum Mechanics. Show all posts
Showing posts with label Quantum Mechanics. Show all posts
Derivation of Planck's Radiation Law
Derivation:
Let $ N$ be the total number of Planck’s oscillators and $E$ be their total energy, then the
average energy per Planck’s oscillator is
$ \overline{E}=\frac{E_{N}}{N}
\qquad (1)$
Let there be $ N_{0}, N_{1} ,N_{2}
,N_{3},---N_{n}$ oscillator having energy $ E_{0}, E_{1}, E_{2}, -- E_{n}$
respectively.
According to Maxwell’s distribution, the number of oscillators in the $ n^{th}$ energy
state is related to the number of oscillators in the ground state by
$ N_{n}=N _{0} e^{\tfrac{-nh\nu }{kt} }\qquad (2)$
Where
$ n$ is a positive integer. So put $ n= 1,2,3,…….$. The above equation can be
written for different energy states. i.e.
$ N_{1}=
N _{0} e^{\tfrac{-h\nu }{kt} }$
$ N_{2}=
N _{0} e^{\tfrac{-2h\nu }{kt} }$
$ N_{3}=
N _{0} e^{\tfrac{-3h\nu }{kt} }$
$.............$
$.............$
So, the total number of Planck’s Oscillators –
$ N= N _{0} +N_{1}+N_{2}+N_{3}+.... N_{n}$
Let $ x = e^{\frac{-h\nu }{kt}} \qquad (4) $
Then $ N = N_{0}[1+x+x^{2}+x^{3}+...+ x^{n}]$
$ N = \frac{N_{0}}{1-x} \qquad(5)$ [ from Binomial theorem]
Now the total energy of oscillators –
From equation $(4)$ put $ x = e^{\tfrac{-h\nu }{kt}}$ in above equation. i.e
$ E_{N } = N_{0}h\nu (x+2x^{2}+3x^{3}+...+nx^{n}) $
$ E_{N } = N_{0}h\nu x(1+2x+3x^{2}+....)$
$ E_{N } = \frac{N_{0}h\nu x}{(1-x)^{2}} \qquad(6)$ (from Bionomical theorem)
Now substituting the value of $N$ from equation $ (5)$ and $ E_{n}$ from equation
$ (6)$ in equation $ (1)$ –
$ \overline{E}= \frac{\frac{N_{0}h\nu x}{(1-x)^{2}}}{\frac{N_{0}}{(1-x)}}$
$ \overline{E}= \frac{h\nu }{(\frac{1}{x}-1)}$
$ \overline{E}= \frac{h\nu }{e^{\tfrac{h\nu }{kt}}-1} \qquad(7)$
The
number of oscillators per unit volume in wavelength range to $ ( \lambda + d\lambda )$ is $\frac{8\pi }{\lambda ^{4}} d\lambda$.
The energy per unit volume $ (E_{\lambda }d\lambda )$ in the wavelength range to $( \lambda
+d\lambda ) $ is –
$ E_{\lambda}d\lambda = \frac{8\pi }{\lambda ^{4}}d\lambda \overline{E} \qquad(8)$
From equation $ (7)$ and $ (8)$ –
$ E_{\lambda}d\lambda = \frac{8\pi }{\lambda ^{4}}d\lambda \frac{h\nu }{(e^{\tfrac{h\nu}{kt}}-1)}$
$ E_{\lambda}d\lambda = \frac{8\pi hc}{\lambda ^{5}} \frac{d\lambda}{(e^{\tfrac{hc}{\lambda kt}}-1)}$
The above equation describes Planck’s radiation law and this law was able to thoroughly explain the black body radiation spectrum.
Wien’s Displacement law from Planck’s Radiation Law:
Planck’s radiation law gives the energy in wavelength region $ \lambda to \lambda +d\lambda $ as –
$ E_{\lambda}d \lambda = \frac{8\pi hc}{\lambda ^{5}}(\frac{1}{e^{\tfrac{hc}{\lambda kt}}-1})d\lambda \qquad(1)$
For shorter wavelength $ \lambda T$ will be small and hence
$ e^{\tfrac{hc}{\lambda kt}}> > 1$
Hence, for a small value of $\lambda T$ Planck’s formula reduces to -
$ E_{\lambda}d \lambda = \frac{8\pi hc}{\lambda ^{5}}(\frac{1}{e^{\tfrac{hc}{\lambda kt}}})
d\lambda$
$ E_{\lambda}d\lambda = \frac{8\pi hc}{\lambda ^{5}}e^{\tfrac{-hc}{\lambda kt}}d\lambda$
$E_{\lambda}d\lambda = A \lambda ^{-5} e^{\tfrac{-hc}{\lambda kt}}d\lambda$
Where $ A = 8\pi hc$
The above equation is Wien’s law of energy distribution verified by Planck
radiation law.
Rayleigh-Jeans law from Planck’s Radiation Law:
According to Planck’s radiation law –
$ E_{\lambda}.d\lambda = \frac{8\pi hc}{\lambda ^{5}}\frac{1 }{e^{\tfrac{hc}{\lambda
kt}}-1}.d\lambda$
For longer wavelength $ e^{\frac{hc}{\lambda kt}}$ is small and can be expanded as-
$ e^{\tfrac{hc}{\lambda kt}} = 1+\frac{hc}{\lambda kt}+\frac{1}{2!}(\frac{hc}{\lambda kt})^{2}+....$
Neglecting the higher-order term –
$ e^{\tfrac{hc}{\lambda kt}} = 1+\frac{hc}{\lambda kt}$
Hence for longer wavelength, Planck’s formula reduces to –
$ E_{\lambda}.d\lambda = \frac{8\pi kt}{\lambda ^{5}}[\frac{1}{1+\frac{hc}{\lambda kt}-1}]$
$ E_{\lambda}.d\lambda = \frac{8\pi kt}{\lambda ^{4}}.d\lambda$
This is Rayleigh Jean’s law verified by Planck Radiation Law.
$ N= N _{0} + N_{0} e^{\tfrac{-h\nu }{kt}}+ N_{0} e^{\tfrac{-2h\nu
}{kt}}+...+ N_{0}e^{\tfrac{-nh\nu }{kt}}$
$ N= N _{0}[1+e^{\tfrac{-h\nu }{kt}}+e^{\tfrac{-2h\nu }{kt}}+.... e^{\tfrac{-nh\nu }{kt}}] \qquad(3)$
$ E_{N} = E_{0}N_{0}+ E_{1}N_{1}+ E_{2}N_{2}+...+ E_{n}N_{n}$
$ E_{N } = 0.N_{0}+ h\nu N_{0} e^{\tfrac{-h\nu }{kt}}+...+nh\nu N_{0} e^{\tfrac{-nh\nu }{kt}}$
$ E_{N } = N_{0}h\nu (e^{\tfrac{-h\nu }{kt}}+2e^{\tfrac{-2h\nu }{kt}}+...+ ne^{\tfrac{-nh\nu }{kt}})$
Orthogonality of the wave functions of a particle in one dimension box or infinite potential well
Description of Orthogonality of the wave functions of a particle in one dimension box or infinite potential well:
Let $\psi_{n}(x)$ and $\psi_{m}(x)$ be the normalized wave functions of a particle in the interval $(0, L)$ corresponding to the different energy level $E_{n}$ and $E_{m}$ respectively. These wave functions are:
$\psi_{n}(x)= \sqrt{\frac{2}{L}} sin \frac{n \pi x}{L}$
$\psi_{m}(x)= \sqrt{\frac{2}{L}} sin \frac{m \pi x}{L}$
Where $m$ and $n$ are integers.
In this function are real. Therefore
$\psi_{n}^{*}(x) = \psi_{n}(x)$
$\psi_{m}^{*}(x) = \psi_{m}(x)$
Where $m=n$,
$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx =0$
Hence, The function is mutually orthogonal in the interval $(0, L)$. These functions $\psi_{n}(x)$ and $\psi_{m}(x)$ are also normalized in this interval. The wave function, which is normalized and mutually orthogonal in an interval is said to form an orthogonal set in this interval. Since the wave function are zero outside the interval $(0, L)$, they are also orthogonal wave function in the whole range of $x$ axis in the interval $(-\infty, +\infty)$.
$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx = \frac{2}{L} \int_{0}^{L} sin \frac{m \pi x}{L} . sin \frac{n \pi x}{L} dx$
$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx =\frac{1}{L} \int_{0}^{L} \left[ cos \left\{ \frac{(m-n) \pi x}{L} \right\} - cos \left\{ \frac{(m+n) \pi x}{L} \right\} \right] dx $
$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx =\frac{1}{L} \left[ \frac{L}{\pi(m-n)} sin \left\{ \frac{(m-n) \pi x}{L} \right\} - \frac{L}{\pi(m+n)} sin \left\{ \frac{(m+n) \pi x}{L} \right\} \right]_{0}^{L} $
$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx =\frac{1}{L} \left[ \frac{L}{\pi(m-n)} sin \left\{ \frac{(m-n) \pi x}{L} \right\} - \frac{L}{\pi(m+n)} sin \left\{ \frac{(m+n) \pi x}{L} \right\} \right]_{0}^{L} $
Normalization of the wave function of a particle in one dimension box or infinite potential well
Description of Normalization of the wave function of a particle in one dimension box or infinite potential well:
We know that the wave function for the motion of the particle along the x-axis is
$\psi_{n}(x)= A \: sin \left( \frac{n \pi x}{L} \right) \quad \left\{ Region \quad 0 \lt x \lt a \right\}$
$\psi_{n}(x)= 0 \quad \left\{ Region \quad 0 \gt x \gt a \right\}$
The total probability that the particle is somewhere in the box must be unity. Therefore,
$\int_{0}^{L} \left| \psi_{n}(x)\right|^{2}dx =1$
Now substitute the value of the wave function in the above equation. Then
$\int_{0}^{L} \left| A \: sin \left( \frac{n \pi x}{L} \right) \right|^{2}dx =1$
$\int_{0}^{L} A^{2} \: sin^{2} \left( \frac{n \pi x}{L} \right) dx =1$
$ \frac{A^{2}}{2}\int_{0}^{L} \left[ 1- cos \left( \frac{2n \pi x}{L} \right) \right] dx =1$
$ \frac{A^{2}}{2} \left[ x - \left( \frac{L}{2n\pi} \right) sin \left( \frac{2n \pi x}{L} \right) \right]_{0}^{L} =1$
$ \frac{A^{2}}{2} \left[ L - \left( \frac{L}{2n\pi} \right) sin \left( \frac{2n \pi L}{L} \right) \right] =1$
$ \frac{A^{2}}{2} \left[ L - \left( \frac{L}{2n\pi} \right) sin \left( 2n \pi \right) \right] =1$
$ \frac{A^{2}}{2} \left[ L - \left( \frac{L}{2n\pi} \right) sin \left( 2n \pi \right) \right] =1$
$ \frac{A^{2}}{2} \left[ L - 0 \right] =1 \qquad(\because sin2n\pi =0)$
$ \frac{A^{2} L}{2} =1$
$ A= \sqrt{\frac{2}{L}}$
Hence, the normalized wave function
$\psi_{n}(x)=\sqrt{\frac{2}{L}} sin \left( \frac{n \pi x}{L} \right)$
The absolute square $\left| \psi_{n}(x) \right|^{2}$ of the wave function $\psi_{n}(x)$ gives the probability density. Hence
$\left| \psi_{n}(x) \right|^{2} = \frac{2}{L} sin^{2} \left( \frac{n \pi x}{L} \right)$
The wave function for the particle in a box can be viewed in analogy with standing waves on a string. The wave function for a standing wave that has nodes at endpoints is of the form $\psi_{n}(x)= A \: sin \left( \frac{n \pi x}{L} \right)$. The condition for a standing wave can also be expressed in terms of wavelength.
$\lambda_{n}=\frac{2 \pi}{k_{n}}$
$\lambda_{n}=\frac{2 \pi}{\frac{n \pi}{L}} \qquad \left( \because k_{n}=\frac{n \pi}{L} \right)$
$\lambda_{n}=\frac{2 L}{n}$
$L= \frac{n \: \lambda_{n}}{2}$
So,
$L= \frac{\: \lambda_{1}}{2} \qquad \left( for \: n=1 \right)$
$L= \lambda_{2} \qquad \left( for \: n=2 \right)$
$L= \frac{3 \: \lambda_{3}}{2} \qquad \left( for \: n=3 \right)$
$L= 2 \lambda_{4} \qquad \left( for \: n=4 \right)$
Geo structure of wave function $\psi_{n}(x)$ and wave function's density $\left| \psi_{n}(x) \right|^{2}$.
Variation of the wave function and probability of finding the particle in a one-dimensional box:
We know that normalised wave function $\psi_{n}(x)$
$\psi_{n}(x)=\sqrt{\frac{2}{L}} sin \left( \frac{n \pi x}{L} \right)$
The probability density of wave function $\left| \psi_{n}(x) \right|$
$\left| \psi_{n}(x) \right|^{2} = \frac{2}{L} sin^{2} \left( \frac{n \pi x}{L} \right)$
Maximum Condition:
The values of $\psi_{n}(x)$ and $\left| \psi_{n}(x) \right|^{2}$ will be maximum. When
$sin \left( \frac{n \pi x}{L} \right)=1$
$sin \left( \frac{n \pi x}{L} \right )=sin \frac{\left( 2m+1 \right) \pi}{2}$
$ \frac{n \pi x}{L} =\left( 2m+1 \right) \frac{ \pi}{2}$
$ x =\left( 2m+1 \right) \frac{ L}{2n}$
Minima Condition:
The values of $\psi_{n}(x)$ and $\left| \psi_{n}(x) \right|^{2}$ will be minima. When
$sin \left( \frac{n \pi x}{L} \right)=0$
$sin \left( \frac{n \pi x}{L} \right)= \sin \: m\pi$
$ \frac{n \pi x}{L} = \: m\pi$
$x=m\left( \frac{L}{n} \right)$
de-Broglie Concept of Matter wave
Louis de-Broglie thought that similar to the dual nature of light, material particles must also possess the dual character of particle and wave. This means that material particles sometimes behave as particle nature and sometimes behave like a wave nature.
According to de-Broglie –
According to Planck’s theory of radiation–
$E=h\nu \qquad(1) $
Where
h – Planck’s constant
$\nu $ - frequency
According to Einstein’s mass-energy relation –
$E=mc^ {2} \qquad (2)$
According to de Broglie's hypothesis equation $ (1)$ and equation $(2)$ can be written as –
$mc^ {2} = h \nu$
$mc^ {2} = \frac{hc}{\lambda }$
$\lambda =\frac{h}{mc}\qquad(3) $
$\lambda =\frac{h}{P}$
Where $P$ –Momentum of Photon
Similarly from equation $(3)$ the expression for matter waves can be written as
Here $P$ is the momentum of the moving particle.
1.) de-Broglie Wavelength in terms of Kinetic Energy
$K=\frac{1}{2} mv ^{2}$
$K=\frac{m^{2}v^{2}}{2m}$
$K=\frac{P^{2}}{2m}$
$P=\sqrt{2mK}$
Now substitute the value of $P$ in equation $ (4)$ so
2.) de-Broglie Wavelength for a Charged particle
The kinetic energy of a charged particle is $K = qv$
Now substitute the value of $K$ in equation$(5)$ so
3.) de-Broglie Wavelength for an Electron
The kinetic energy of an electron
$K=ev$
If the relativistic variation of mass with a velocity of the electron is ignored then $m=m_{0}$ wavelength
So wavelength of de-Broglie wave associated with the electron in non-relativistic cases
4.) de-Broglie wavelength for a particle in Thermal Equilibrium
For a particle of mass $m$ in thermal equilibrium at temperature $T@
$K=\frac{3}{2}kT$
Where $K$ – Boltzmann Constant
$\lambda =\frac{h}{\sqrt{2m.\frac{3}{2}kt}}$
Properties of matter wave →
A moving particle is always associated with a wave, called as de-Broglie matter-wave, whose wavelengths depend upon the mass of the particle and its velocity.
h – Planck’s constant
$\nu $ - frequency
| $\lambda=\frac{h}{mv}=\frac{h}{P}\qquad(4)$ |
| $\lambda =\frac{h}{\sqrt{2mK}} \qquad (5)$ |
| $\lambda =\frac{h}{\sqrt{2mqv}}$ |
| $\lambda =\frac{h}{\sqrt{2m_{0}ev}}$ |
| $\lambda =\frac{h}{\sqrt{3mKT}}$ |
- Matter waves are generated only if the material's particles are in motion.
- Matter-wave is produced whether the particles are charged or uncharged.
- The velocity of the matter wave is constant; it depends on the velocity of material particles.
- For the velocity of a given particle, the wavelength of matter waves will be shorter for a particle of large mass and vice-versa.
- The matter waves are not electromagnetic waves.
- The speed of matter waves is greater than the speed of light.
According to Einstein’s mass-energy relation$E=mc^{2}$$h\nu = mc^{2}$$\nu =\frac{mc^{2}}{h}$Where $\nu$ is the frequency of matter-wave.We know that the velocity of matter-wave$ u =\nu \lambda $
Substitute the value of $\nu$ in the above equation$u =\frac{mc^{2}}{h}. \lambda $
$u =\frac{mc^{2}}{h} . \frac{h}{mv}$$u =\frac{c^{2}}{v}$ Where $v$ → particle velocity which is less than the velocity of light. - The wave and particle nature of moving bodies can never be observed simultaneously.
Group velocity is equal to particle velocity
Prove that: Group velocity is equal to Particle Velocity
Solution:
We know that group velocity
$V_{g}=\frac{d\omega}{dk}$
$V_{g}=\frac{d(2\pi\nu )}{d(\frac{2\pi }{\lambda })} \qquad \left(k=\frac{2\pi}{\lambda} \right)$
$V_{g}=\frac{d\nu}{d(\frac{1}{\lambda })}$
$\frac{1}{V_{g}}=\frac{d( \frac{1}{\lambda })}{d\nu}\qquad(1)$
We know that the total energy of the particle is equal to the sum of kinetic energy and potential energy. i.e
$E=K+V$
Where
$K$ – kinetic energy
$V$ – Potential energy
$E=\frac{1}{2} mv^{2}+V$
$E-V=\frac{1}{2}\frac{(mv)^2}{m}$
$E-V=\frac{1}{2m }(mv)^2$
$2m(E-V)=(mv)^2$
$mv=\sqrt{2m(E-V)}$
According to de-Broglie wavelength-
$\lambda =\frac{h}{mv}$
$\lambda =\frac{h}{\sqrt{2m(E-V)}}$
$\frac{1}{\lambda} =\frac{\sqrt{2m(E-V)}}{h}\qquad(3)$
Now put the value of $\frac{1}{\lambda }$ in equation$(1)$
$\frac{1}{V_{g}} =\frac{d}{dv}[\frac{{2m(E-V)}^\tfrac{1}{2}}{h}]$
$\frac{1}{V_{g}} =\frac{d}{dv}[\frac{{2m(h\nu -V)}^\tfrac{1}{2}}{h}]$
$\frac{1}{V_{g}} =\frac{1}{2h}[{2m(h\nu -V)}]^{\tfrac{-1}{2}}{2m.h}$
$\frac{1}{V_{g}} =\frac{1}{2h}[{2m(E -V)}]^{\tfrac{-1}{2}}{2m.h} \qquad \left(\because E=h\nu \right) $
$\frac{1}{V_{g}} =\frac{m}{mv}$ {from equation $(2)$}
$V_{g}=V$
Thus, the above equation shows that group velocity is equal to particle velocity.
$V$ – Potential energy
Definition and derivation of the phase velocity and group velocity of wave
Wave:
When such type of wave propagates in the medium a progressive change in phase takes place from one particle to the next particle.
Propagation of Wave:
Wave propagation in the medium occurs with two different kinds of velocity. i.e. phase velocity and group velocity.
1. Phase Velocity:
A plane wave traveling in the positive x-direction is represented by
$y=A \: sin \omega (t-\frac{x}{v})$
Where $ \omega $ – angular frequency
$y=A \: sin(\omega t-\frac{\omega x}{v})$
$y=A \: sin(\omega t-kt) \qquad(1)$
For plane-wave $(\omega t-kx)$ is the phase of wave motion. For the plane of constant phase (wavefront). We have
$( \omega t-kx) = constant (\phi) \qquad(2)$
Differentiate with respect to time $(t)$ of the above equation
$ \omega -k.\frac{dx}{dt}=0$
$\frac{dx}{dt}=\frac{ \omega}{k}\qquad(3)$
$V_{p}=\frac{ \omega}{k} \qquad \left [ \because V_{p}= \frac{dx}{dt} \right ]$
Where $V_{p}$ - Phase Velocity of a wave
Question- Show that the phase velocity of matter-wave always exceeds the velocity of light.
Answer-
Method-I
$V_{p}=\frac{ \omega }{k}$
$V_{p}=\frac{2\pi \nu }{\frac{2\pi }{\lambda }}$
$V_{p} = \frac{2 \pi h \nu}{\frac{2 \pi h}{\lambda }}$
$V_{P} = \frac{E}{P}$
$V_{P} =\frac{mc^{2}}{mv}$
$V_{P} =\frac{c^{2}}{v}$
Method-II:
$V_{P}=\nu \lambda$
$V_{P}=\frac{mc^{2}}{h} \frac{h}{mv}$
$V_{P}=\frac{c^{2}}{v}$
Where $v$ is the velocity of matter particles.
Wave packet→
Group Velocity→
Group Velocity also represents the velocity of energy flow or transmission of
information in a traveling wave or wave packet. It is represented by $V_{g}$. So
$V_{g} = \frac{d\omega }{dk}$
Expression for group velocity $(V_{g})$→
Let two plane simple harmonic waves of the same amplitude and slightly different wavelength traveling simultaneously in the positive x-direction in a dispersive medium be represented by –
$y_{1} = A\: sin{(\omega t-kx)} \qquad (1)$
$y_{2}= A\:sin[(\omega +\delta \omega )t-(k+\delta k)x] \qquad (2)$
From the superposition principle the resultant displacement of waves
$y=y_{1}+y_{2}\qquad (3)$
$y=2Asin(\omega t-kx)cos\frac{1}{2}(t\delta \omega –x\delta k) \qquad (4)$
This is the analytical equation for the group of waves. This equation represents the following
points –
$R=2A cos \frac{1}{2}(t \delta\omega-x \delta k) \qquad (5)$
(A) For maximum amplitude→
$ cos\frac{1}{2}(\delta\omega t-x\delta k)=1 \qquad (6) $
Then the resultant amplitude of the wave packet will be
$R_{m}=2A \qquad $ {from equation $(5)$ }
Where
$R_{m}$ - Resultant maximum amplitude
From equation$(6)$-
$cos\frac{1}{2}(t\delta\omega –x\delta k)=1$
$cos\frac{1}{2}(t\delta\omega –x\delta k)=cos0$
$\frac{1}{2}(t\delta\omega –x\delta k)=0$
$\frac{x}{t}=\frac{\delta\omega }{\delta k}$
$V_{g}=\frac{\delta\omega }{\delta k}$
OR
$V_{g}=\frac{d\omega}{dk}$
Thus maximum amplitude i.e. the center of the wave packet moves with velocity $\frac {d\omega}{dk}$ or group velocity.
(B) For minimum amplitude→
Let a wave packet that has minimum (zero) amplitude on two successive points $x_{1}and x_{2}$. So for minimum amplitude at point $x_{1}$ –
$cos\frac{1}{2}(t.\delta \omega –x_{1}.\delta k)=0$
$cos\frac{1}{2}(t.\delta \omega –x_{1}.\delta k)=cos(2n+1)\frac{\pi }{2}$
$\frac{1}{2}(t.\delta \omega –x_{1}.\delta k)=(2n+1)\frac{\pi }{2}$
$t.\delta \omega – x_{1}.\delta k=(2n+1)\pi \qquad(1)$
Similarly minimum amplitude at the second successive point $x_{2}$-
$t\delta \omega –x_{2}.\delta k =(2n-1)\pi \qquad(2)$
Now subtract the equation $(2)$ in equation $(1)$
$(x_{2}-x_{1}).\delta k=2\pi$
$x_{2}-x_{1}=\frac{2\pi}{\delta k}$
$x_{2}-x_{1}=\frac{2\pi}{d(\frac{2\pi}{\lambda})} $
$\delta x=\frac{-\lambda ^{2}}{\delta \lambda }$
Here $\delta x$ -Length of the wave packet
The above equation also can be written as-
$ dx=\frac{-\lambda^{2}}{d \lambda }$
Prove that→
$V_{g}= -\lambda^{2} \frac{d\nu }{d\lambda}$
Where $\nu $ is the frequency and $\lambda $ is the wavelength.
Proof:
We know that
$V_{g}=\frac{d\omega }{dk}$
$V_{g}=\frac{d(2\pi\nu )}{d(\frac{2\pi }{\lambda })} \qquad \left( \because \omega= 2\pi \nu \: and \: k=\frac{2\pi}{\lambda } \right)$
$V_{g}=\frac{2\pi d\nu }{2\pi d( \frac{1}{ \lambda })}$
$V_{g}=-\lambda ^{2}\frac{d\nu }{d\lambda }$
Note:
A moving particle cannot be equal to a single wave train. The speed of a single wave train is called the phase velocity so moving particles are equivalent to a group of waves or wave packets.
A wave is defined as a disturbance in a medium from an equilibrium condition that propagates from one region of the medium to other regions.
The velocity with which plane of constant the phase of a wave propagates through the medium at a certain frequency is called the phase velocity or wave velocity.
A wave packet is an envelope or packet which contains the number of plane waves having different wavelengths or wavenumbers. These numbers of waves superimpose on each other and form constructive and destructive interference over a small region of space and a resultant wave obtain. The spread of amplitude of the resultant wave with distance determines the size of the wave packet. A wave packet is also called a wave group.
 |
The velocity of propagation of wave packet through space is known as group velocity.
$y=A \: sin(\omega t-kx)+ A \: sin[(\omega +\delta \omega)t-(k+\delta k)x]$
$y=A[sin(\omega t-kx)+ sin{(\omega +\delta \omega )t-(k+\delta k )x}]$
- The sine factors represent a carrier wave that travels with the phase velocity.
- The amplitude of the resultant wave is
$(t.\delta \omega – x_{1}.\delta k) – (t.\delta \omega - x_{2}.\delta k)= (2n+1)\pi–(2n-1)\pi $
Product of phase velocity and group velocity is equal to square of speed of light
Prove that $\rightarrow$
Proof →
We know that
$V_{p}=\nu \lambda \qquad(1)$
And de Broglie wavelength-
$\lambda =\frac{h }{mv}\qquad(2)$
According to Einstein's mass-energy relation-
$E=mc^{2}$
$h\nu=mc^{2}$
$\nu=\frac{mc^{2}}{h}\qquad(3)$
Now put the value of $\lambda $ and $\nu $ in equation$(1)$
$V_{p}= [\frac{mc^{2}}{h}] [\frac{h}{mv}]$
$V_{p}=\frac{C^{2}}{v}$
Since group velocity is equal to particle velocity i.e. $V_{g}=v$. So above equation can be written as
$V_{p}=\frac{C^{2}}{V_{g}}$
$V_{p}.V_{g}=C^{2}$
Note →
➢ $V_{g}=V_{p}$ for a non-dispersive medium ( in a non-dispersive medium all the waves travel with
phase velocity).
➢ $V_{g}< V_{p}$ for normal dispersive medium
➢ $V_{g}> V_{p}$ for anomalous dispersive media.
Dispersive medium →
The medium in which the phase velocity varies with wavelength or frequency is called a dispersive medium. In such a medium, waves of different wavelengths travel with different phase velocities.
Non-dispersive medium →
The medium in which the phase velocity does not vary with wavelength or frequency is called a Non-dispersive medium.
Dispersive waves →
Those waves in the medium for which phase velocity varies with wavelength or frequency are called dispersive waves.
Non-dispersive waves →
Those waves in which phase velocity does not vary with wavelength are called non-dispersive waves. So phase velocity independent of wavelength.
The Product of phase velocity and group velocity is equal to the square of the speed of light i.e. $\left( V_{p}.V_{g}=c^{2} \right)$
Energy distribution spectrum of black body radiation
Description→
The energy distribution among the different wavelengths in the spectrum of black body radiation was studied by Lummer and Pringsheim in 1899. There are the following important observations of the study.
- The energy distribution in the radiation spectrum of the black body is not uniform. As the temperature of the body rises the intensity of radiation for each wavelength increases.
- At a given temperature, the intensity of radiation increases with increases in wavelength and becomes maximum at a particular wavelength with further in increases wavelength the intensity of radiation decreases.
- The points of maximum energy shift towards the shorter wavelength as the temperature increases i.e. $\lambda _{m} \times T=constant$. It is also known as Wein’s displacement law of energy distribution.
- For a given temperature the total energy of radiation is represented by the area between the curve and the horizontal axis and the area increases with increases of temperature, being directly proportional to the fourth power of absolute temperatures.
The total amount of heat radiated by a perfectly black body per unit area per unit time is directly proportional to the fourth power of its absolute temperature $(T)$.
$E = \sigma T^{4}$ Where $\sigma$ = Stefan constant having value $\left ({5}\cdot{67}\times{10}^{-8}Wm^{-2}K^{4}\right )$This is called Stefan-Boltzmann's law of energy distribution.
 |
| Energy distribution in the spectrum of black body radiation |
Energy distribution laws of black body radiation
1.) Wein’s laws of Energy distributions→
A.) Wein's Fifth Power law→
The total amount of the energy emitted by a black body per unit volume at an absolute temperature in
the wavelength range $\lambda$ and $\lambda + d\lambda$ is given as
$E\lambda \cdot d\lambda= \frac{A}{\lambda^{5}}f\left ( \lambda T \right ) \cdot d\lambda \qquad (1)$
Where $A$ is a constant and $f(\lambda T)$ is a function of the product $\lambda T$ and is given as
$ f\left ( \lambda T\right )=e^-\frac{hc}{\lambda kT}\qquad (2)$
From equation $(1)$ and $(2)$
$E_\lambda \cdot d\lambda = \frac{A}{\lambda ^{5}}e^\frac{-hc}{\lambda kT} \cdot d\lambda$
$E_\lambda \cdot d \lambda = A \lambda ^{-5} e^\frac{-hc}{\lambda kT} \cdot d \lambda$
Wien’s law energy distribution explains the energy distribution at the short wavelength at higher
temperatures and fails for long wavelengths.
B.) Wein's Displacement law→
As the temperature of the body is raised the maximum energy shift toward the shorter wavelength i.e.
$\lambda_{m} \times T = Constant $
Where
$\lambda_m$- Wavelength at which the energy is maximum
$T$-Absolute temperature
Thus, if radiation of a particular wavelength at a certain temperature is adiabatically altered to another wavelength then temperature changes in the inverse ratio.
2.) Rayleigh-Jean’s law→
The total amount of energy emitted by a black body per unit volume at an absolute temperature T in the wavelength range $\lambda $ and $\lambda +d\lambda $ is given as
$E_{\lambda}.d\lambda = \frac{8\pi kt}{\lambda ^{4}}.d\lambda$
Where K– Boltzmann’s Constant which has valve $ 1.381\times 10^{23}\frac{J}{K}$
This law, explains the energy distribution at the longer wavelength at all temperatures and fails totally for the shorter wavelength.
Note→
The energy distribution curves of the black body show a peak while going towards the ultraviolet wavelength (shorter $ \lambda $) and then fall while Rayleigh-Jeans law indicates continuous rise only. This is the failure of classical physics.
3.) Stefan-Boltzmann Law→
The total amount of heat radiated by a perfectly black body per unit area per second is directly proportional to
the fourth power of its absolute temperature $(T)$. i.e.
$E \propto T^{4}$
$E = \sigma T^{4}$
Where $\sigma$= Stefan’s Constant which has value $5.67\times 10^{-8} W-\frac{K^{4}}{m^{2}}$
It is a black body at absolute temperature $T$ is surrounded by another black body at absolute temperature $T_{0}$, The net amount of heat $E$ lost by the former per second per $cm^{2}$ is→
$E=\sigma (T^{4}-T_{0}^{^{4}})$
$\lambda_m$- Wavelength at which the energy is maximum
$T$-Absolute temperature
Relation between group velocity and phase velocity
We know that phase velocity
$V_{p}=\frac{\omega }{k}$
$\omega =V_{p}.k \qquad(1)$
And group velocity
$V_{g}=\frac{d\omega}{dk} \qquad(2)$
Substitute the value of $\omega$ from equation$(1)$ in equation $(2)$
$V_{g}=\frac{d}{dk}(V_{p}.k)$
$V_{g}=V_{p}+k.\frac{dV_{p}}{dk}$
$V_{p}=V_{p}+k.\frac{dV_{p}}{d\lambda}.\frac{d\lambda }{dk} \qquad (3)$
But
$\lambda=\frac{2\pi }{k}$
The above equation can be obtain from following formula i.e. $k=\frac{2\pi}{\lambda }$
Now put the value of $\lambda$ in equation $(3)$
$V_{g}=V_{p}+k\frac{dV_{p}}{d\lambda}\frac{d}{dk}(\frac{2\pi }{k}$
$V_{g}=V_{p}+k\frac{dV_{p}}{d\lambda}(\frac{-2\pi }{k^{2}}$
$V_{g}=V_{p}-\frac{2\pi}{k}\frac{dV_{p}}{d\lambda }$
$V_{g}=V_{p}-\lambda\frac{dV_{p}}{d\lambda }$
Thus, the above equation represents the relation between group velocity and phase velocity.
Assumptions of Planck’s Radiation Law
Planck in 1900 suggested the correct explanation of the black body radiation curve. They gave the following assumption →
If an oscillator is vibrating with a frequency $ \nu $ it can only radiate in quanta of magnitude $h\nu $ i.e. “The oscillator can have only discrete energy value $E_{n}$ ” given by–
$E_{n}=nh\nu$
Where
$n$ – an integer
$h$– Planck ’s constant and the value is $6.626\times10^{-34} J-s$
The average energy of Planck’s oscillator of frequency $\nu$ -
$E_{\lambda}d\lambda = \frac{8\pi hc}{\lambda ^{5}} \frac{d\lambda }{(e^{\frac{hc}{\lambda kT}}-1)}$
$E_{\nu}d\nu= \frac{8\pi h\nu^{3}}{c^{3}}\frac{d\nu }{(e^{\frac{h\nu}{kt}}-1)}$
This assumption is most revolutionary in character. This implies that the exchange of energy between radiation and matter (Black lamp or platinum Coating ) cannot take place continuously but are limited to a discrete set of value $ 0, h\nu, 2h\nu, 3h\nu,------ nh \nu $.
- A chamber contains black body energy radiation and simple harmonic oscillators (atoms of Wall, i.e. Black lamp & Platinum coating inside wall, behave as oscillators or resonators) of molecular dimensions which can vibrate with all possible frequencies.
- The frequency of energy radiation emitted by an oscillator is the same as the frequency of its vibration.
- An oscillator cannot emit or absorb the energy in a continuous manner it can emit or absorb energy in a small unit (packet) called Quanta.
$n$ – an integer
$h$– Planck ’s constant and the value is $6.626\times10^{-34} J-s$
Heisenberg uncertainty principle
If the x-coordinate of the position of a particle is known to an accuracy of $\delta x$, then the x-component of momentum cannot be determined to an accuracy better than $\Delta P_{x}\approx \frac{\hbar }{\Delta x}$.
$\Delta P_{x}. \Delta x\approx \hbar$
The above inequality must be satisfied
$\Delta P_{x}. \Delta x\geqslant \hbar$
Where $\hbar $ - Planck’s Constant
This is the Uncertainty principle with macroscopic objects.
Exact statement of the Uncertainty principle →
The product of the uncertainties in determining the position and momentum of the particle can never be smaller than the number of the order $\frac{\hbar }{2}$.
$\Delta P_{x}. \Delta x\geqslant \frac{\hbar}{2}$
Where $\delta x$ and $\delta P $ are defined as the root mean square deviation from their mean values.
The Uncertainty principle can also describe by the following formula →
$\Delta x.\Delta p_{x}\approx \frac{\hbar}{2}$
$\Delta x.\Delta p_{x}\geqslant \frac{\hbar}{2}$
$\Delta x.\Delta p_{x}\geqslant \frac{h}{4\pi }$
Expression for $y$ and $z$ component →
$\Delta y.\Delta p_{y}\geqslant \frac{h}{4\pi }$
$\Delta z.\Delta p_{z}\geqslant \frac{h}{4\pi }$
The uncertainty relation between energy and time →
$\Delta E.\Delta t\geqslant \frac{h}{4\pi }$
$\Delta E.\Delta t\geqslant \frac{\hbar }{2 }$
The uncertainty relation between momentum and Angular Position→
$\Delta L.\Delta \theta \geqslant \frac{h }{4\pi }$
$\Delta L.\Delta \theta \geqslant \frac{\hbar}{2}$
Mathematical equation of wave function of a free particle in simple harmonic motion
Periodic motion:
If a particle repeats its motion or path at a regular interval of time, it is known as periodic motion.
Simple Harmonic Motion:
Simple harmonic motion (S.H.M.) is a specific type of periodic motion. In the simple harmonic motion, the force (i.e., restoring force) exerted on the particle is directly proportional to its displacement from the equilibrium position and acts in the opposite direction to that displacement.
Wave:
A wave is the combination of infinite simple harmonic motion equations.
Mathematical Equation:
Let us consider a particle that is doing simple harmonic motion in a circular path with radius $A$. Let at any instant $t$ particle move from position $P_{1}$ to $P_{2}$. So vector resolution of position $P_{2}$ is (as shown in the figure below):
Horizontal Component i.e. $x$ component of position vector $P_{2}$:
$x=A sin(\omega t - \phi) \qquad (1)$
Vertical Component i.e. $y$ component of position vector $P_{2}$:
$y=A cos (\omega t - \phi) \quad (2)$
According to Max Born's hypothesis-
"A wave is described by a wave function $\varphi$, which is mathematically expressed in the form of a complex quantity."
So mathematical representation of a wave function
$\varphi= x+iy \qquad (3)$
Now put the value of $x$ and $y$ component in the above equation-
$\varphi= A sin (\omega t - \phi)+ i A cos (\omega t - \phi) $
$\varphi=A [sin (\omega t - \phi)+ i cos (\omega t - \phi) ]$
$\varphi=A e^ {i(\omega t - \phi)} \qquad (4)$
Where $\phi$is the phase of the wave. The value of $\phi$ can be found by the relation between the phase difference and path difference of a plane progressive wave.
$\phi =\frac {2\pi}{\lambda}\cdot x $
$\phi = k\cdot x$
Now put the value of $\phi$ from the above equation into equation $(4)$. So the wave function equation can be written as
$\varphi (x,t) =A e^ {i(\omega t - k \cdot x)} \qquad (5)$
Let us consider a particle having mass $m$ that is in motion along the positive x-direction with momentum $p$ and total energy $E$. So the wave function equation $(5)$ in terms of momentum and total energy
$\psi(x,t)=Ae^{-i\omega (t-\frac{x}{v})} \qquad(6) $
$\psi(x,t )=Ae^{-i(\omega t-kx)}$
$\psi(x,t )=Ae^{i(kx-\omega t)} \qquad(7)$
According to Planck’s hypothesis-
$E=h\nu \qquad(8) $
$E=\frac{h}{2 \pi }\cdot 2 \pi \nu$
$E=\hbar.\omega$
$\omega=\frac{E}{\hbar } \qquad(9)$
According to de Broglie hypothesis-
$\lambda= \frac{h}{p}$
$p =\frac{h}{\lambda }$
$p =\frac{h}{2 \pi }\cdot \frac{2 \pi}{\lambda}$
$p=\hbar\cdot k$
$k=\frac{p}{\hbar}\qquad(10)$
Now put the value of $\omega$ and $k$ from equation $(9)$ and equation $(10)$in equation$(7)$
$\psi (x,t)=Ae^{ i(\frac{p}{\hbar }x-\frac{E}{\hbar }t)}$
$\psi (x,t )=Ae^{\frac{i}{\hbar}(px-Et)}$
The equation for the three-dimensional $(3D)$ wave function of a free particle:
$\psi (\overrightarrow{r},t)=Ae^{\frac{i}{\hbar}(\overrightarrow{p}x-Et)}$
 |
| Simple harmonic motion of a particle |
 |
| Propagation of a wave along the x-axis |
Normalized and Orthogonal wave function
Description:
We know that $\psi^{*}\psi$ or $\left|\psi \right|^{2} d\tau $ represent the probability of finding the particle in volume element $d\tau$.
The total probability of finding the particle in the entire space is 1 so
$ \int \left|\psi(r,t) \right|^{2} d\tau=1 $
Where integral extends overall space.
$\int \psi^{*}(r,t) \psi(r,t) d\tau=1$
A wave function satisfies the above equation so it is called normalized to unity.
For any wave function that is a solution of the time-dependent Schrodinger equation
$\int \psi^{*} \psi d\tau=N$
$\frac{1}{N} \int \psi^{*} \psi d\tau=1$
$\int \frac{\psi{*}}{\sqrt{N}} \frac{\psi}{\sqrt{N}} d\tau = 1$
Where
$\sqrt{N}$ → Normalized Factor
$\frac{\psi}{N} $ → Normalised wave function
If independent coordinate $x$,$y$,$z$, and $\psi$ satisfy the Schrodinger wave equation. Then it is evident that $\frac{\psi}{\sqrt {N}}$ also satisfies the Schrodinger wave equation.
If $\psi_{i}$ and $\psi_{j}$ are two different wave functions both the satisfactory solution of the wave equation for a given system. Then these functions will be normalized if
$\psi_{i}^{*} \psi_{i} d\tau=1 \quad and \quad \psi_{j}^{*} \psi_{j} d\tau=1$
If the two wave function $\psi_{i}$ and $\psi_{j}$ are the satisfactory solution of the wave equation for a given system. Then these functions will be mutually orthogonal if
$\psi_{i}^{*} \psi_{j} d\tau=0 \qquad Where \: $i \neq j$
$\psi_{j}^{*} \psi_{i} d\tau=0 \qquad Where \: $i \neq j$
These integral vanishes over the entire space.
$\sqrt{N}$ → Normalized Factor
$\frac{\psi}{N} $ → Normalised wave function
Quantum Mechanical Operators
Operator →
An operator is defined as a mathematical term that is used in the operation of a function so that this function may or may not be transformed into another function.
Operators of Quantum Mechanics →
There are the following quantum mechanical operators which are used in the wave function of particles:-
Momentum Operator
Kinetic Energy Operator
Total Energy Operator (Hamiltonian Operator)
Total Energy Operator in terms of the differential with respect to time
Momentum Operator →
The wave function for a free particle moving along the position $x$-direction is
$\psi(x,t)=A e^{\frac{i}{\hbar}(P_{x}x-Et)}$
Differentiate the above equation with respect to $x$ then we get
$\frac{\partial \psi}{\partial x}= A e^{\frac{i}{\hbar}(P_{x}x-Et)} \frac{i}{\hbar} P_{x} $
$\frac{\partial \psi}{\partial x}= \psi \frac{i}{\hbar} P_{x} $
$ P_{x} \psi = \frac{\hbar}{i}\frac{\partial \psi}{\partial x}$
$ P_{x} = \frac{\hbar}{i}\frac{\partial}{\partial x}$
For three dimensional:-
$\overrightarrow{P}= \frac{\hbar}{i} \overrightarrow{\nabla}$
Kinetic Energy Operator →
We know that the momentum operator
$ P_{x} \psi = \frac{\hbar}{i}\frac{\partial \psi}{\partial x} \qquad(1)$
Differentiate the above equation $(1)$ with respect to $x$ then we get
$ P_{x} \frac{\partial \psi}{\partial x} = \frac{\hbar}{i}\frac{\partial^{2} \psi}{\partial x^{2}} \qquad(2)$
Now substitute the value of $\frac{\partial \psi}{\partial x}$ from equation $(1)$ to equation $(2)$
$\frac{\hbar}{i}\frac{\partial^{2} \psi}{\partial x^{2}} = P_{x} \frac{i}{\hbar} P_{x} \psi$
$\frac{\hbar^{2}}{i^{2}}\frac{\partial^{2} \psi}{\partial x^{2}} = P_{x}^{2} \psi$
$ -\hbar^{2}\frac{\partial^{2} \psi}{\partial x^{2}} = P_{x}^{2} \psi \qquad (\because i^{2}=-1)$
$ -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \psi}{\partial x^{2}} = \frac{P_{x}^{2}}{2m} \psi \qquad {3}$
$ -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \psi}{\partial x^{2}} = K \psi \qquad (\because \frac{P_{x}^{2}}{2m} = K)$
$ K \psi = -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \psi}{\partial x^{2}} $
$ K = -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} $
For three dimensions:-
$ K = -\frac{\hbar^{2}}{2m}\nabla^{2} $
Total Energy Operator (Hamiltonian Operator) →
The total energy of the particle moving along $x4-aix is given by
$E=\frac{P_{x}^{2}}{2m} + V(x) \qquad(1)$
Where V(x) → Potential Energy
We know that the kinetic energy operator
$ K = -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} $
$ \frac{P_{x}^{2}}{2m} = -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} \qquad (\because K=\frac{P_{x}^{2}}{2m})$
Now substitute the value of $ \frac{P_{x}^{2}}{2m}$ in equation$(1)$
$E= -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} + V(x)$
Multiply $\psi$ on the both side of above equation
$E \psi= -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \psi }{\partial x^{2}} + V(x) \psi$
$E \psi= \left [ -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} + V(x) \right ] \psi$
$E \psi= \hat{H} \psi$
So the total energy operator
$ \hat{H} = \left [ -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} + V(x) \right ] $
For three dimensions:-
$\hat{H} = \left [ -\frac{\hbar^{2}}{2m}\nabla^{2} + V(x) \right ] $
The total energy operator is denoted by $\hat{H}$ and called the Hamiltonian Operator.
Total Energy Operator in terms of the differential with respect to time →
We know that the wave function
$\psi= A e^{\frac{i}{\hbar}}\left( P_{x}x - Et \right)$
Differentiate the above equation $(1)$ with respect to $t$ then we get
$\frac{\partial \psi}{\partial t}= A e^{\frac{i}{\hbar}(P_{x} x -Et)} \frac{i}{\hbar} (-E) $
$\frac{\partial \psi}{\partial t}= - \frac{i}{\hbar} E \psi $
$E \psi= -\frac{\hbar}{i} \frac{\partial \psi}{\partial t}$
$E \psi= i^{2} \frac{\hbar}{i} \frac{\partial \psi}{\partial t} \qquad (\because i^{2}=-1)$
$E \psi= i \hbar \frac{\partial \psi}{\partial t}$
This energy operator is denoted by $E$ so
$E = i \hbar \frac{\partial }{\partial t}$
Postulate of wave mechanics or Quantum Mechanics
Postulate of Wave or Quantum Mechanics (or Operator formalism in Quantum mechanics) →
The formulation of mathematical equations of quantum mechanics is based on the linear operator. This operator formulation of quantum mechanics is known as postulates of quantum mechanics. These postulates are given below:-
- For a system consisting of particles moving in a field of a conservative force, there is an associated complex wave function $\psi(x, y, z, t)$ where $x$,$y$,$z$ space coordinates, and $t$ is the time. This wave function enables us to obtain a description of the behavior of the system, consistent with the principle of uncertainty.
- There is an operator with every observable dynamical quantity. The operator corresponding to the pertinent dynamical quantities is:-
Dynamical Variable Symbol Quantum Mechanical Operator Position $x$
$y$
$z$$x$
$y$
$z$Momentum $P_{x}$
$P_{y}$
$P_{z}$
Generalised Form $\overrightarrow{P}$$\frac{\hbar}{i}\frac{\partial}{\partial x}$
$\frac{\hbar}{i}\frac{\partial}{\partial y}$
$\frac{\hbar}{i}\frac{\partial}{\partial z}$
Generalised Form $\frac{\hbar}{i}\overrightarrow{\nabla}$Total Energy $E$ $i\hbar \frac{\partial}{\partial t}$ Total Energy $E$ $-\frac{\hbar^{2}}{2m} \nabla^{2}+V(x)$
This is also known as Hamiltonian Operator $H$.Kinetic Energy $K$ $-\frac{\hbar^{2}}{2m} \nabla^{2}$ Potential Energy $V(x,y,z)$ $V(x,y,z)$ All the operators have eigen functions and eigen values. - The wave function $\psi(x,y,z,t)$ and its partial derivatives $\frac{\partial \psi}{\partial x}$, $\frac{\partial \psi}{\partial y}$, $\frac{\partial \psi}{\partial z}$ must be finite, continuous and single-valued for all values of $x$, $y$, $z$ and $t$
- The product of $\psi(x,y,z,t)$ and $\psi^{*}(x,y,z,t)$ is always a real quantity. The product is called the probability density and $\psi\psi^{*} d\tau $ is interpreted as a probability that the particle will be found in volume element $d\tau$ at $x$,$y$,$z$ and time $t$. Since the total probability of finding particles somewhere in the entire space must be equal to 1.
$\int_{-\infty}^{+\infty} \psi \: \psi^{*}\: d\tau = 1$The integral is taken overall space.
- The average or expectation value of an observable quantity $\alpha$ with which an operator $\hat{\alpha}$ is associated is defined by
$\left< \alpha \right> = \int_{-\infty}^{+\infty} \psi^{*} \hat{\alpha} \psi d\tau$
Eigenfunction, Eigenvalues and Eigenvectors
Eigenfunction and Eigenvalues →
If $\psi$ is a well-behaved function, then an operator $\hat{P}$ may operate on $\psi$ in two different ways depending upon the nature of function $\psi$ `
Eigenvalues and Eigenvectors →
Let a linear transformation equation
$AX=\lambda X \qquad(1)$
Where
A → Square matrix of $n$ order (where $n=1,2,3,.....$)
$\lambda$ → Scalar Factor
The equation $(1)$ may be written as
$AX=I\lambda X$
$AX-I\lambda X=0$
$(A-I\lambda)X=0 \qquad(2)$
Where $I$ is unit matrix
Any value of $\lambda$ for which equation $(1)$ or equation $(2)$ has non zero (i.e $X \neq 0$) solution is called eigenvalues or characteristic roots or latent root of the matrix $A$ and corresponding non zero solution of $X$ is called eigenvectors or characteristic vectors or latent vectors of the matrix $A$
The matrix $\left| A- \lambda I \right|$ is called characteristic matrix of $A$. The determinant $\phi(\lambda) = \left| A- \lambda I \right|$ is called the characteristic polynomial of $A$. So
$\phi(\lambda) = \left| A- \lambda I \right| =0$
And $\phi(x)= a_{0}+a_{1} \lambda a_{2} \lambda^{2}+ .......+a_{n} \lambda^{n}=0 $
- When an operator $\hat{P}$ operates on any function $\psi$ then this function $\psi$ changes into another function $\phi$. i.e.
$\hat{P} \psi =\phi$Where $\phi$ is a new function linearly depending upon the initial function $\psi$.Example:Let us consider a function $f(x)=x^{2}$ and an operator ie. differential operator $\frac{d}{dx}$ is operate on the function. Then we get$\frac{d}{dx}f(x)= \frac{d}{dx} (x^{2})$$\frac{d}{dx}f(x)= 2x$Now the given function $f(x)=x^{2}$ change into another function $f(x)=x$.
-
When an operator $\hat{P}$ operates on any function $\psi$ then this function $\psi$ does not change into another function but now this function $\psi$ may be with multiples of complex or real numbers(or values).i.e
$\hat{P} \psi =\lambda \phi$Where $\lambda$ is Real OR Complex Number. This number or value is known as Eigenvalues.In this case, the function $\psi$ is a member of the class of physically meaningful functions called the eigen function of the operator $\hat{P}$. The number $\lambda$ is called the eigen value of operator $\hat{P}$ associated with eigen function $\psi$ and this equation is known as the eigenvalue equation.Example: Let us consider a function $f(x)=e^{2x}$ and an operator ie. differential operator $\frac{d}{dx}$ is operate on the function. Then we get$\frac{d}{dx}f(x)= \frac{d}{dx} (e^{2x})$$\frac{d}{dx}f(x)= 2e^{2x}$Now the given function $f(x)=e^{2x}$ change into another function $f(x)=x$.
A → Square matrix of $n$ order (where $n=1,2,3,.....$)
$\lambda$ → Scalar Factor
Physical interpretation of the wave function
We have assumed that the wave associated with a particle in motion is represented by a complex variable quantity called the wave function $\psi(x,t)$. Therefore, it can not have a direct physical meaning. Since it is a complex quantity, it may be expressed as
$\psi(x,y,z,t)=a+ib \qquad(1)$
Where $a$ and $b$ are real functions of the variable $(x,y,z,t)$. The complex conjugate of wave function $\psi(x,y,z,t)$
$\psi^{*}(x,y,z,t)=a-ib \qquad(2)$
Multiply equation $(1)$ and equation $(2)$
$\psi(x,y,z,t).\psi^{*}(x,y,z,t)=a^{2}+b^{2} \qquad(3)$
$ \left| \psi(x,y,z,t) \right|^{2}=a^{2}+b^{2} \qquad(4)$
If $\psi \neq 0$ Then the product of $\psi$ and $\psi^{*}$ is real and positive. Its positive square root is denoted by $\left|\psi(x,y,z,t) \right|$, and it is called the modulus of $\psi$.
The quantity $ \left| \psi(x,y,z,t) \right|^{2}$ is called the probability density $(P)$. So for the motion of a particle, the probability of finding the particle in the region $d\tau$ will be:
$\int {P d\tau}= \int {\psi(x,y,z,t).\psi^{*}(x,y,z,t).d\tau}=\int {\left| \psi(x,y,z,t) \right|^{2}d\tau}$
Here $P$ are the probability that tells us that the particle will be found in a volume element $d\tau(=dx.dy.dz)$ surrounding the point at position $(x,y,z)$ at time $t$.
For the motion of a particle in one dimension, the probability of finding the particle in the region $dx$ will be:
$\int{P dx}= \int {\psi(x,t).\psi^{*}(x,t).dx}=\int {\left| \psi(x,t) \right|^{2}dx}$
Particle in one dimensional box (Infinite Potential Well)
Let us consider a particle of mass $m$ that is confined to one-dimensional region $0 \leq x \leq L$ or the particle is restricted to move along the $x$-axis between $x=0$ and $x=L$. Let the particle can move freely in either direction, between $x=0$ and $x=L$. The endpoints of the region behave as ideally reflecting barriers so that the particle can not leave the region. A potential energy function $V(x)$ for this situation is shown in the figure below.
The potential energy inside the one -dimensional box can be represented as
$\begin{Bmatrix}
V(x)=0 &for \: 0\leq x \leq L \\
V(x)=\infty & for \: 0> x > L \\
\end{Bmatrix}$
$\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2m}{\hbar^{2}}(E-V)\psi(x)=0 \qquad(1)$
If the particle is free in a one-dimensional box, Schrodinger's wave equation can be written as:
$\frac{d^{2} \psi(x)}{d x^{2}}+\frac{2mE}{\hbar^{2}}\psi(x)=0$
$\frac{d^{2} \psi(x)}{d x^{2}}+\frac{8 \pi^{2} mE}{h^{2}}\psi(x)=0 \quad (\because \hbar=\frac{h}{2 \pi}) \quad(2)$
$\frac{d^{2} \psi(x)}{d x^{2}}+ k^{2}\psi(x)=0 \quad (\because k^{2}=\frac{8 \pi^{2} mE}{h^{2}}) \quad(3)$
The general solution of the above differential equation $(2)$
$\psi(x)= A sin(kx)+ B cos(kx) \qquad(4)$
The wave function $\psi(x)$ should be zero everywhere outside the box since the probability of finding the particle outside the box is zero. Similarly, the wave function $\psi(x)$ must also be zero at walls of the box because the probability density $[\psi(x)]^{2}$ must be continuous. Thus, the boundary conditions for this problem is that
(i) $\psi(x)=0$ For $x=0$
(ii) $\psi(x)=0$ For $x=L$
Now applying the boundary condition in equation$(4)$ i.e.
(i) At $x=0$ the wave function $\psi(0)=0$
Now we get
$\psi(0)= A sin(k.0)+ B cos(k.0)$
$A sin(k.0)+ B cos(k.0)=0 \qquad (\because \psi(0)= 0)$
$B=0$
Hence substitute the value of $B$ in equation$(4)$ ,
$\psi(L)= A sin(kx) \qquad(5)$
Now applying the second boundary condition:
(ii) At $x=L$ the wave function $\psi(L)=0$, we get
$\psi(x)= A sin(kL) \qquad(6)$
This equation will satisfy only for certain values of $k$, say $k_{n}$. Since $A$ can not be taken zero hence
$sin(k_{n}L)=0 $
$sin(k_{n}L)=sin(n\pi) $
$k_{n}L=n\pi $
$k_{n}=\frac{n\pi}{L} \qquad(7)$
Thus for each allowed values of $k_{n}$ there is a wave function $\psi(x)$ given as, using equation$(5)$ and equation$(7)$
$\psi_{n}(x)=A sin(\frac{n\pi x}{L})$
This is the expression of the wave function or eigen function for a particle in a box.
Now, from equation $(3)$ and equation$(7)$, we get
$k^{2}=\frac{8 \pi^{2} mE}{h^{2}}= (\frac{n \pi}{L})^{2}$
$E=\frac{n^{2} h^{2}}{8mL^{2}}$
This is the expression of energy or eigen value for a particle in a box.
In general, the expression for this energy is written as:
$E_{n}=\frac{n^{2} h^{2}}{8mL^{2}}$
For different values of $n$ energy values can be written as
For $n=1$
$E_{1}=\frac{h^{2}}{8mL^{2}}$
It is known as zero-point energy or ground energy state
For $n=2$
$E_{2}=\frac{2^{2} h^{2}}{8mL^{2}}=2^{2}E_{1}$
For $n=3$
$E_{3}=\frac{3^{2} h^{2}}{8mL^{2}}=3^{2}E_{1}$
For $n=4$
$E_{4}=\frac{4^{2} h^{2}}{8mL^{2}}=4^{2}E_{1}$
So generalized form of the above equation can be written as
$E_{n}=n^{2}E_{1}$
Some of the possible energies for a particle in a box are shown on an energy-level diagram in the figure below.
The energy levels have a spacing that increases with increasing $n$ and thus the particle in a box can take only certain discrete energy values, called Eigen-values. This means that the energy levels of a particle in a box are quantized but according to classical mechanics, the particle may take any continuous range of energy values between zero and infinity.
 |
Particle in One-Dimensional Box(Infinite Potential Well) |
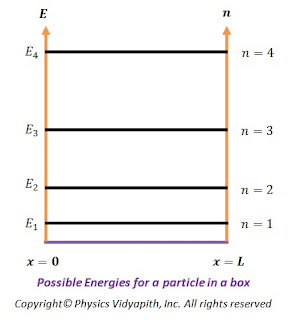 |
Possible Energies for a particle in a box |
Popular Posts
-
Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is ...
-
Angle of Acceptance → "If incident angle of light on the core for which the incident angle on the core-cladding interface equals t...
-
Derivation of interference of light due to a wedge-shaped thin film: Interference of light due to wedge-shaped thin film The wedge...
-
Maxwell's Equations: Maxwell's equation of the electromagnetic wave is a collection of four equations i.e. Gauss's law of elec...
-
Let a plane wavefront be incident normally on slit $S_{1}$ and $S_{2}$ of equal $e$ and separated by an opaque distance $d$.The diffracted l...
Study-Material
Categories
Alternating Current Circuits
(10)
Atomic and Molecular Physics
(4)
Biomedical
(1)
Capacitors
(6)
Classical Mechanics
(12)
Current carrying loop in magnetic field
(5)
Current Electricity
(10)
Dielectric Materials
(1)
Electromagnetic Induction
(3)
Electromagnetic Wave Theory
(23)
Electrostatic
(22)
Energy Science and Engineering
(2)
Error and Measurement
(2)
Gravitation
(11)
Heat and Thermodynamics
(3)
Kinematics Theory Of Gases
(2)
Laser System & Application
(15)
Magnetic Effect of Current
(9)
Magnetic Substances
(3)
Mechanical Properties of Fluids
(5)
Nanoscience & Nanotechnology
(4)
Nuclear Physics
(7)
Numerical Problems and Solutions
(2)
Optical Fibre
(5)
Optics
(25)
Photoelectric Effect
(3)
Quantum Mechanics
(37)
Relativity
(8)
Semiconductors
(2)
Superconductors
(1)
Topic wise MCQ
(9)
Units and Dimensions
(1)
Waves
(5)





