Operator →
An operator is defined as a mathematical term that is used in the operation of a function so that this function may or may not be transformed into another function.
Operators of Quantum Mechanics →
There are the following quantum mechanical operators which are used in the wave function of particles:-
Momentum Operator
Kinetic Energy Operator
Total Energy Operator (Hamiltonian Operator)
Total Energy Operator in terms of the differential with respect to time
Momentum Operator →
The wave function for a free particle moving along the position $x$-direction is
$\psi(x,t)=A e^{\frac{i}{\hbar}(P_{x}x-Et)}$
Differentiate the above equation with respect to $x$ then we get
$\frac{\partial \psi}{\partial x}= A e^{\frac{i}{\hbar}(P_{x}x-Et)} \frac{i}{\hbar} P_{x} $
$\frac{\partial \psi}{\partial x}= \psi \frac{i}{\hbar} P_{x} $
$ P_{x} \psi = \frac{\hbar}{i}\frac{\partial \psi}{\partial x}$
$ P_{x} = \frac{\hbar}{i}\frac{\partial}{\partial x}$
For three dimensional:-
$\overrightarrow{P}= \frac{\hbar}{i} \overrightarrow{\nabla}$
Kinetic Energy Operator →
We know that the momentum operator
$ P_{x} \psi = \frac{\hbar}{i}\frac{\partial \psi}{\partial x} \qquad(1)$
Differentiate the above equation $(1)$ with respect to $x$ then we get
$ P_{x} \frac{\partial \psi}{\partial x} = \frac{\hbar}{i}\frac{\partial^{2} \psi}{\partial x^{2}} \qquad(2)$
Now substitute the value of $\frac{\partial \psi}{\partial x}$ from equation $(1)$ to equation $(2)$
$\frac{\hbar}{i}\frac{\partial^{2} \psi}{\partial x^{2}} = P_{x} \frac{i}{\hbar} P_{x} \psi$
$\frac{\hbar^{2}}{i^{2}}\frac{\partial^{2} \psi}{\partial x^{2}} = P_{x}^{2} \psi$
$ -\hbar^{2}\frac{\partial^{2} \psi}{\partial x^{2}} = P_{x}^{2} \psi \qquad (\because i^{2}=-1)$
$ -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \psi}{\partial x^{2}} = \frac{P_{x}^{2}}{2m} \psi \qquad {3}$
$ -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \psi}{\partial x^{2}} = K \psi \qquad (\because \frac{P_{x}^{2}}{2m} = K)$
$ K \psi = -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \psi}{\partial x^{2}} $
$ K = -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} $
For three dimensions:-
$ K = -\frac{\hbar^{2}}{2m}\nabla^{2} $
Total Energy Operator (Hamiltonian Operator) →
The total energy of the particle moving along $x4-aix is given by
$E=\frac{P_{x}^{2}}{2m} + V(x) \qquad(1)$
Where V(x) → Potential Energy
We know that the kinetic energy operator
$ K = -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} $
$ \frac{P_{x}^{2}}{2m} = -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} \qquad (\because K=\frac{P_{x}^{2}}{2m})$
Now substitute the value of $ \frac{P_{x}^{2}}{2m}$ in equation$(1)$
$E= -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} + V(x)$
Multiply $\psi$ on the both side of above equation
$E \psi= -\frac{\hbar^{2}}{2m}\frac{\partial^{2} \psi }{\partial x^{2}} + V(x) \psi$
$E \psi= \left [ -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} + V(x) \right ] \psi$
$E \psi= \hat{H} \psi$
So the total energy operator
$ \hat{H} = \left [ -\frac{\hbar^{2}}{2m}\frac{\partial^{2} }{\partial x^{2}} + V(x) \right ] $
For three dimensions:-
$\hat{H} = \left [ -\frac{\hbar^{2}}{2m}\nabla^{2} + V(x) \right ] $
The total energy operator is denoted by $\hat{H}$ and called the Hamiltonian Operator.
Total Energy Operator in terms of the differential with respect to time →
We know that the wave function
$\psi= A e^{\frac{i}{\hbar}}\left( P_{x}x - Et \right)$
Differentiate the above equation $(1)$ with respect to $t$ then we get
$\frac{\partial \psi}{\partial t}= A e^{\frac{i}{\hbar}(P_{x} x -Et)} \frac{i}{\hbar} (-E) $
$\frac{\partial \psi}{\partial t}= - \frac{i}{\hbar} E \psi $
$E \psi= -\frac{\hbar}{i} \frac{\partial \psi}{\partial t}$
$E \psi= i^{2} \frac{\hbar}{i} \frac{\partial \psi}{\partial t} \qquad (\because i^{2}=-1)$
$E \psi= i \hbar \frac{\partial \psi}{\partial t}$
This energy operator is denoted by $E$ so
$E = i \hbar \frac{\partial }{\partial t}$
Postulate of wave mechanics or Quantum Mechanics
Postulate of Wave or Quantum Mechanics (or Operator formalism in Quantum mechanics) →
The formulation of mathematical equations of quantum mechanics is based on the linear operator. This operator formulation of quantum mechanics is known as postulates of quantum mechanics. These postulates are given below:-
- For a system consisting of particles moving in a field of a conservative force, there is an associated complex wave function $\psi(x, y, z, t)$ where $x$,$y$,$z$ space coordinates, and $t$ is the time. This wave function enables us to obtain a description of the behavior of the system, consistent with the principle of uncertainty.
- There is an operator with every observable dynamical quantity. The operator corresponding to the pertinent dynamical quantities is:-
Dynamical Variable Symbol Quantum Mechanical Operator Position $x$
$y$
$z$$x$
$y$
$z$Momentum $P_{x}$
$P_{y}$
$P_{z}$
Generalised Form $\overrightarrow{P}$$\frac{\hbar}{i}\frac{\partial}{\partial x}$
$\frac{\hbar}{i}\frac{\partial}{\partial y}$
$\frac{\hbar}{i}\frac{\partial}{\partial z}$
Generalised Form $\frac{\hbar}{i}\overrightarrow{\nabla}$Total Energy $E$ $i\hbar \frac{\partial}{\partial t}$ Total Energy $E$ $-\frac{\hbar^{2}}{2m} \nabla^{2}+V(x)$
This is also known as Hamiltonian Operator $H$.Kinetic Energy $K$ $-\frac{\hbar^{2}}{2m} \nabla^{2}$ Potential Energy $V(x,y,z)$ $V(x,y,z)$ All the operators have eigen functions and eigen values. - The wave function $\psi(x,y,z,t)$ and its partial derivatives $\frac{\partial \psi}{\partial x}$, $\frac{\partial \psi}{\partial y}$, $\frac{\partial \psi}{\partial z}$ must be finite, continuous and single-valued for all values of $x$, $y$, $z$ and $t$
- The product of $\psi(x,y,z,t)$ and $\psi^{*}(x,y,z,t)$ is always a real quantity. The product is called the probability density and $\psi\psi^{*} d\tau $ is interpreted as a probability that the particle will be found in volume element $d\tau$ at $x$,$y$,$z$ and time $t$. Since the total probability of finding particles somewhere in the entire space must be equal to 1.
$\int_{-\infty}^{+\infty} \psi \: \psi^{*}\: d\tau = 1$The integral is taken overall space.
- The average or expectation value of an observable quantity $\alpha$ with which an operator $\hat{\alpha}$ is associated is defined by
$\left< \alpha \right> = \int_{-\infty}^{+\infty} \psi^{*} \hat{\alpha} \psi d\tau$
Eigenfunction, Eigenvalues and Eigenvectors
Eigenfunction and Eigenvalues →
If $\psi$ is a well-behaved function, then an operator $\hat{P}$ may operate on $\psi$ in two different ways depending upon the nature of function $\psi$ `
Eigenvalues and Eigenvectors →
Let a linear transformation equation
$AX=\lambda X \qquad(1)$
Where
A → Square matrix of $n$ order (where $n=1,2,3,.....$)
$\lambda$ → Scalar Factor
The equation $(1)$ may be written as
$AX=I\lambda X$
$AX-I\lambda X=0$
$(A-I\lambda)X=0 \qquad(2)$
Where $I$ is unit matrix
Any value of $\lambda$ for which equation $(1)$ or equation $(2)$ has non zero (i.e $X \neq 0$) solution is called eigenvalues or characteristic roots or latent root of the matrix $A$ and corresponding non zero solution of $X$ is called eigenvectors or characteristic vectors or latent vectors of the matrix $A$
The matrix $\left| A- \lambda I \right|$ is called characteristic matrix of $A$. The determinant $\phi(\lambda) = \left| A- \lambda I \right|$ is called the characteristic polynomial of $A$. So
$\phi(\lambda) = \left| A- \lambda I \right| =0$
And $\phi(x)= a_{0}+a_{1} \lambda a_{2} \lambda^{2}+ .......+a_{n} \lambda^{n}=0 $
- When an operator $\hat{P}$ operates on any function $\psi$ then this function $\psi$ changes into another function $\phi$. i.e.
$\hat{P} \psi =\phi$Where $\phi$ is a new function linearly depending upon the initial function $\psi$.Example:Let us consider a function $f(x)=x^{2}$ and an operator ie. differential operator $\frac{d}{dx}$ is operate on the function. Then we get$\frac{d}{dx}f(x)= \frac{d}{dx} (x^{2})$$\frac{d}{dx}f(x)= 2x$Now the given function $f(x)=x^{2}$ change into another function $f(x)=x$.
-
When an operator $\hat{P}$ operates on any function $\psi$ then this function $\psi$ does not change into another function but now this function $\psi$ may be with multiples of complex or real numbers(or values).i.e
$\hat{P} \psi =\lambda \phi$Where $\lambda$ is Real OR Complex Number. This number or value is known as Eigenvalues.In this case, the function $\psi$ is a member of the class of physically meaningful functions called the eigen function of the operator $\hat{P}$. The number $\lambda$ is called the eigen value of operator $\hat{P}$ associated with eigen function $\psi$ and this equation is known as the eigenvalue equation.Example: Let us consider a function $f(x)=e^{2x}$ and an operator ie. differential operator $\frac{d}{dx}$ is operate on the function. Then we get$\frac{d}{dx}f(x)= \frac{d}{dx} (e^{2x})$$\frac{d}{dx}f(x)= 2e^{2x}$Now the given function $f(x)=e^{2x}$ change into another function $f(x)=x$.
A → Square matrix of $n$ order (where $n=1,2,3,.....$)
$\lambda$ → Scalar Factor
Kepler's Laws of Planetary Motion
Kepler's Laws →
Kepler's found important uniformity in the motion of the planets. This uniformity is known as "Kepler's Laws of planetary motion".
There are basically three laws →
First law (Law of orbits) →
Second Law (Law of Areal Speed) →
According to the second law, When the planet is farthest from the sun, then its speed is maximum, and when it is nearest the sun, then its speed is maximum.
From the above figure, A planet is moving around the sun from $A$ to $B$ in a given time interval, and from $C$ to $D$ in the same time interval, then according to the law of areal speed, the areas $ASB$ and $CSD$ will be equal with respect to the same time-interval
Proof →
Let us consider, A planet moves the angle $d\theta$ from $A$ to $B$ in the infinitesimal interval of time $dt$, then the area swept out by radial line $SA$ is
$dA$= Area of the curved $\Delta$ $SAB$
$dA \approx \frac{1}{2} \left( AB \times SA \right)$
$dA \approx \frac{1}{2} \left( r \: d\theta \times r \right)$
$dA \approx \frac{1}{2} \left( r^{2} \: d\theta \right)$
Thus, the instantaneous areal speed of the planets is
$\frac{dA}{dt}=\frac{1}{2} r^{2} \frac{d \theta}{dt}$
$\frac{dA}{dt}=\frac{1}{2} r^{2} \omega \qquad(1)$
Where $\omega$ → The angular speed of the planet.
We know that
$J=I \: \omega$
Where $I$ is the instantaneous moment of inertia of the planet about the Sun $S$.
$J=m \: r^{2} \: \omega \qquad(2)$
Where $m$ is the mass of the planet. Now substitute the value of $r^{2} \: \omega$ from equation $(2)$ in equation $(1)$.
$\frac{dA}{dt}=\frac{J}{2m} \left( Constant \right)$
From the above equation, The areal speed $\frac{dA}{dt}$ of the planet is constant which is Kepler's Second Law. The above equation shows that the angular momentum of the planet is constant. i.e. The angular momentum of any planet is conserved.
Third Law (Law of Periods) →
Proof →
Let $a$ and $b$ be the semi-major and semi-minor axes of the ellipse, then the area of the ellipse will be $\pi ab$. Let $T$ is the period of one complete revolution of any planet, then
$T=\frac{Area \: of \: the \: ellipse}{Areal \: Speed}$
$T=\frac{\pi a b}{\frac{J}{2m}}$
$T=\frac{2\pi a b m}{J}$
$T^{2}=\frac{4 \pi^{2} a^{2} b^{2} m^{2}}{J^{2}}$
Let $l$ be the semi-latus rectum of the elliptical orbit i.e. $l=\frac{b^{2}}{a}$. Then we get the above equation which can be written as
$T^{2}=\frac{4 \pi^{2} m^{2} a^{3} l }{J^{2}}$
$T^{2} \propto a^{3} $
Where $\frac{4 \pi^{2} m^{2} l }{J^{2}}$ is constant.
From the above equation, It is clear that the larger the distance of a planet from the sun, the larger will be its period of revolution around the sun. The period of revolution of the nearest planet to the sun i.e. Mercury is $88$ days, while that of the faraway planet from the sun i.e. Pluto is $248$ years.
- First law (Law of orbits)
- Second Law (Law of Areal Speed)
- Third Law (Law of Periods)
All the planets move around the sun in elliptical path and the sun is at the one foci of the ellipse.
A line joining the any planet to sun sweeps out equal areas in equal interval of of times. i.e The areal speed of the planets remains constant.
 |
| Planetary Motion |
The square of the time period of one complete revolution of any planet around the sun is directly proportional to the cube of the semi-major axis of its elliptical orbit.
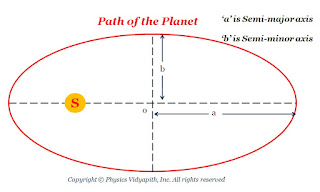 |
| Path of the Planet |
Relation between gravitational acceleration and gravitational force
Relation between $g$ and $G$ →
Let us consider:
The mass of earth = $M_{e}$
The radius of earth = $R_{e}$
The mass of the object = $m$
If the object is placed on the surface of the earth then the gravitational force on the object is →
$F=G \frac{M_{e} m}{R_{e}^{2}} \qquad(1)$
The force on the object due to gravitational acceleration is →
$F=mg \qquad(2)$
From equation $(1)$ and equation $(2)$
$mg=G \frac{M_{e} m}{R_{e}^{2}}$
$g=G \frac{M_{e}}{R_{e}^{2}}$
$G M_{e}=g R_{e}^{2}$
The mass of earth = $M_{e}$
The radius of earth = $R_{e}$
The mass of the object = $m$
Newton's law for Gravitational Force
Gravitational Force →
Newton's Gravitational Law statement is a combination of three individual statements. These are
$F\propto \frac{m_{1} \: m_{2}}{r^{2}}$
$F=G \frac{m_{1} \: m_{2}}{r^{2}}$
Where $G$ is Newton's gravitaional constant and its experimental value $6.67\times 10^{-11} \frac{N-m^{2}}{kg^{2}}$
Properties of Newton's law for Gravitational force →
There are the following properties of Newton's law for gravitational force
Gravitational force is always an attractive force.
Gravitational force is action and reaction pair and follows Newton's third law.
A Gravitational force is a conservative force.
Gravitational force is central force i.e. it is always acting along the line joining between two particles.
Unit and Dimensional formula of $G$
The unit of $G$ is $\frac{N-m^{2}}{kg^{2}}$
The dimensional Formula of $G$ is $[M^{-1}L^{3}T^{-2}]$
- The force between the two-particle is directly proportional to the product of their masses i.e.
$F \propto m_{1} \: m_{2} \qquad(1)$Where $m_{1}$ & $m_{2}$ are the masses of the particles. - The force between the two-particle is inversely proportional to the square of the distance between them i.e.
$F \propto \frac{1}{r^{2}} \qquad(2)$Where $r$ is the distance between the particles. - This force always acts between the line joining the masses.
Frame of References (Inertial Frame and Non Inertial Frame)
It is assumed that space is continuous and the motion of particles in space can be described by their position at different instants of time. The position of a particle is known as a point in space. These points are described by the coordinate system in space.
Absolute Space:
The absolute space is those frame of reference relative to which every motion and position should be measured.
Types of Frame of Reference:
According to the motion of particles frame of reference is divided into two categories
$F=ma \qquad (1)$
$F=0$
so from equation $(1)$
$ ma=0$
$ a=0$
$ \frac{d^2r}{dt^2}=0\qquad (2)$
In component form, above equation, can be written as:
$ \frac{d^2x}{dt^2}=0;\:\:\:\frac{d^2y}{dt^2}=0;\:\:\:\frac{d^2z}{dt^2}=0\qquad (3)$
Discussion of Inertial Frame in terms of relative frame of reference:
Let us consider an inertial frame $S$ and another frame $S'$ which is moving with constant velocity $v$ relative to frame $S$. If the position of the origins of the two frames coincide, then in the two frames the position vector of any particle $P$ at any instant $t$ can be related by the following expression-
$ \overrightarrow{r}=\overrightarrow{oo'}+\overrightarrow{r'}$
$ \overrightarrow{r}=\overrightarrow{v}t+\overrightarrow{r'} \qquad \left \{ {\overrightarrow{oo}'=\overrightarrow{v}t} \right \}$
Differentiate the above equation
$\frac{d\overrightarrow{r}}{dt}=\overrightarrow{v}+\frac{d\overrightarrow{r'}}{dt}$
Again differentiate the above equation
$\frac{d^2\overrightarrow{r}}{dt^2}=\frac{d^2\overrightarrow{r'}}{dt^2}$
$a=a'$
Now we conclude that "If a frame is an inertial frame then all those frames which are moving with constant velocity relative to the first frame are also inertial"
Non-inertial Frame:
According to Newton's Second Law, the force $F$ applied on a body of mass $m$ is given by
$ F_{i}=ma_{i}\qquad (1)$
Newton's Second Law is not valid when a body of mass $m$ self accelerated and accelerated body will observe the acceleration $a_{N}$. Hence
$ F_{i}\neq ma_{N}\qquad (2)$
If no external force is acting on a particle. Even then in the accelerated frame, It will appear that a force is acting on it. This force is called pseudo force or fictitious force. The direction of force is opposite to acceleration.
$ F_{o}\neq ma_{o}\qquad (3)$
Discussion of Non-inertial Frame in term of relative frame of reference:
Let us consider, an inertial frame $S$ and another frame $S'$ is moving with an acceleration $a_{0}$ relative to frame $S$.
$ \overrightarrow{r_{i}}=\overrightarrow{r_{N}}+\frac{1}{2}a_{0}t^{2}$
Differentiate the above equation with respect to $'t'$
$ \frac{d\overrightarrow{r_{i}}}{dt}=\frac{d\overrightarrow{r_{N}}}{dt}+a_{0}t$
Again differentiate the above equation with respect to $'t'$
$ \frac{d^{2}\overrightarrow{r_{i}}}{dt^{2}}=\frac{d^{2}\overrightarrow{r_{N}}}{dt^{2}}+a_{0}$
$ a_{i}=a_{N}+a_{0}$
$ a_{i}-a_{0}=a_{N}$
$ ma_{i}-ma_{0}=ma_{N}$
$F_{i}+F_{0}=F_{N}$
This formula gives the observed force $F_{N}$ in the accelerated system.
When point (position of particle in space) and the time are taken together then it is called an Event.
The coordinate system of a particle which describe the position of any particle relative to it, then such coordinate system is known as Frame of Reference or System of Reference.
- Inertial frame of reference
- Non-inertial frame of reference
Those unaccelerated frame of reference, in which Newton's first and second laws hold, are called inertial frames.In an inertial frame, body does not experience any force so according to second law of Newton-
 |
| Inertial Frame of Reference |
Those frames of reference in which Newton's law of inertia does not hold are called non-inertial frames.All the accelerated and rotating frames are the non-inertial frames of reference.
 |
| Non-inertial Frame of Reference |
Characteristics, Advantages, Disadvantages and Applications of Ruby Laser
Characteristics of Ruby Laser →
Some of the characteristics of ruby laser are given as follows:
The Advantages of Ruby Laser →
Some advantages of ruby laser are mentioned below:
The disadvantage of Ruby Laser →
Following are some disadvantages of Ruby laser:
Applications of Ruby Laser →
Ruby laser have declined in use with the discovery of a better lasing medium but they are still used in a number of applications some of which are given as follows:
Spiking in Ruby Laser →
Ruby laser is a three-level pulsed laser. The operation of ruby laser leads to a pulsed output with flash lamps as pumping source. The output of a ruby laser is found to consist of a series of pulses of duration of a microsecond or less. The output of this laser is a highly irregular function of time with the intensity having random amplitude fluctuation of varying duration as shown in the figure. These pulses of the short duration are called spikes and the phenomenon is called laser spiking. Duration of individual spikes is of the order of $0.1-1 \mu s$, the time interval between two adjacent spikes is about $1-10 \mu s$. The power of each spike is of the order of $10^{4}- 10^{5} W$. The characteristic spiking of ruby laser
The Characteristic Spiking of Ruby Laser →
When the pumping source (flash lamp) is turned on the population at the upper level gradually increases while the population at the lower energy level decreases. The duration of the exciting flashlight is of the order of milliseconds and may be sufficiently intense to build up population inversion very rapidly. As soon as the population at the upper level becomes sufficiently large and the threshold condition is reached, laser action starts producing a laser pulse. Due to laser pulsed emission population of upper laser level is depleted more rapidly than it can be restored by flashlight. This process leads to leads to an interruption of laser oscillations, the laser oscillation ceases for a few microseconds. Because the flash lamp is still active it again builds up population inversion and laser oscillations beings causing other spikes and the sequence is repeated. A series of pulses is thus produced itself till the intensity of the flashlight has fallen below the threshold value due to which it is not possible to rebuild the necessary population inversion and the lasing action stops.
- Ruby laser is the first working laser that was developed in 1960.
- Ruby lasers are three-level solid-state pulsed lasers with pulse lengths of the order of a millisecond.
- This laser uses a synthetic Ruby crystal that is Aluminium oxide as its gain medium.
- A triply ionized chromium $$Cr^{+3} is used as a dopant for active ion, concentration bring of the order of $0.055%$.
- Ruby crystals are hard and durable, chemically stable and it has good thermal conductivity.
- Ruby lasers are optically pumped using a flash lamp.
- In a ruby laser, water or liquid nitrogen is used as a coolant.
- These lasers produce pulses of visible light at wavelength $6928A^{\circ}$ and $6943A^{\circ}$, with $6943A^{\circ}$ as dominant wavelength which is a deep red color.
- Ruby laser is highly temperature-dependent.
- A practical ruby laser operates at about $1%$ efficiency.
- Pulse repetition rate is comparatively low, of the order of $1$ to $2$ pulse per second.
- Ruby laser is very easy to construct and operate.
- A very strong and intense laser beam up to an output power of $10^{4}- 10^{6} W$, is generated in this laser.
- It has a degree of coherence.
- Ruby crystal is hard, durable and it has good thermal conductivity and coherence length.
- It is chemically very stable.
- The laser crystal can be grown with a high degree of optical quality.
- Ruby cannot be grown in large dimensions.
- Ruby laser is less directional and has very small efficiency.
- High excitation energy is required as more than half of the active centers are to be excited to achieve population inversion
- It has a very small operation for only a few hours.
- producers pulsed output of microsecond duration($\approx30 \mu s$).
- Very high heat is produced in these lasers due to which an effective cooling system is required.
- In these lasers, only a small part of pumping power is utilized in the excitation of chromium ion $Cr^{+3}$ and the rest goes to heat up to apparatus.
- These lasers are used in optical holography to produce holographic portraits, in size up to a meter square.
- These lasers are used in tattoo and hair removal but are being replaced by other lasers.
- These lasers are used in the measurement of plasma properties such as electron density temperature etc.
- These lasers are used where short pulses of red light are required.
- These lasers are used in labs to create holograms of large objects such as aircraft tires to look for weaknesses in the lining.
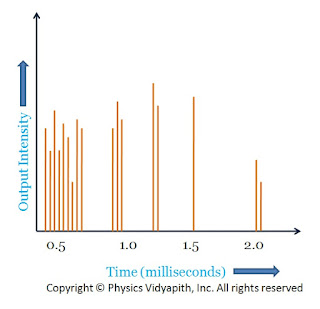 |
| Spiking in Ruby Laser |
Principle, Construction and Working of the Ruby Laser
Principle of Ruby Laser →
Ruby laser is the first working laser that was invented by T.H.Maima in 1960. It is a three-level solid-state pulsed laser that uses a synthetic ruby crystal or sapphire$(Al_{2}O_{3})$ as its gain medium and triply ionized chromium$(Cr^{+3})$ is used as a dopant.
Construction of Ruby Laser →
There are the following main components of ruby laser:
1. Active Medium →
The active medium or gained medium in ruby laser is a synthetic ruby crystal or Aluminium oxide $(Al_{2}O_{3})$ in the form of a cylindrical rod having size $2-30cm$ in length and $0.5-2.0cm$ in diameter. The size of the rod main varies depending upon the use. This gain medium falls in the category of 'narrow line width' laser material. A triply ionised chromium $(Cr^{+3})$ is used as doping material or dopant which works as an active ion. For doping of ruby $(Al_{2}O_{3})$, chromium oxide $(Cr_{2}O_{3})$ is mixed as impurity in ruby and small fraction of aluminium ion $(Al^{+3})$ in ruby are replaced by chromium ions $(Cr^{+3})$. The concentration of chromium ions $(Cr^{+3})$ is of the order of $0.055%$ and at this concentration, the number of chromium ions $(Cr^{+3})$ per cubic meter is nearly $10^{25}$. It is the chromium ions $(Cr^{+3})$ that population is set up in ruby laser and gives rise to the laser action. The chromium ions $(Cr^{+3})$ are active centers and provide the energy levels for both lasing transitions and pumping. The host Aluminium oxide $(Al_{2}O_{3})$ itself does not participate directly in lasing action.
2. Resonant Cavity →
The ends of the ruby are optically flat and parallel and then silvered, one end completely and the other only partially. The one end of the rod acts as fully reflecting and another one as partially reflecting. The reflectors can be plane-parallel or with a slight curvature, curved mirrors being more useful for compensating the thermal lensing of the rod which takes place during the pumping cycle. The space between the end faces is known as a resonant cavity in which light intensity can be built up or amplified by multiple reflections.
The ends of the ruby rod are polished with great precision, such that the ends are flat to within a quarter of a wavelength of the output light and parallel to each other within a few seconds of arc. The rod with its reflecting ends acts as a Fabry Perot resonator. Modern laser often uses rods with ends cut and polished at "Brewster's Angle" to eliminate the reflections from the ends of the rod.
3. Pumping and cooling Device →
In the ruby laser, population inversion is done by optical pumping. Xenon flash lamps provide the most efficient operation of ruby lasers with a pulse duration ranging from milliseconds. The ruby rod is wound by a helical xenon flashlight tube with an excitation source in the form of a power supply. The pumping absorption bands are at $4000 A^{\circ}$ and $5500 A^{\circ}$ with an approximation bandwidth of $500 A^{\circ}$ at each of the wavelengths. Pulses of energies up to $100J$ can be obtained through the pulse repetition rate is comparatively low, of the order of one to two pulses per second which limit the average power. Ruby laser requires high pumping flux to get population inversion due to which a considerable amount of heat is generated during laser operation. Ruby laser being highly temperature-dependent requires an arrangement of effective cooling. Water cooling of the rod combined with the higher thermal conductivity of Ruby provides a sufficient cooling effect to remove the excess heat. For this purpose, water is circulated in a glass tube surrounding the laser system. Being transparent in the wavelength region of pumping bands water does not affect the pumping flux from the flash lamp before it gets absorbed by Ruby road. Liquid nitrogen is also used as a coolant material in ruby lasers.
Working(Lasing Action) of Ruby Laser →
The energy level diagram of chromium ion in ruby is shown in the figure below:
The energy level $E_{3}$ has two main pump bands or excited bands $T_{1}$ and $T_{2}$ having a bandwidth of nearly $800A^{\circ}$. The energy level $E_{2}$ which is known as the metastable state in ruby has a double energy level $A_{1}$ and $A_{2}$. These energy levels are separated by nearly $14A^{\circ}$. These are the twofold degenerate energy level.
In the normal state, The chromium ions are in-ground energy state $E_{1}$. When light from the flash lamp is made to fall upon the ruby rod the incident radiation is absorbed by chromium ions and rises to an excited state $E_{3}$. The chromium ions in the ground state can absorb a photon of wavelength $5500A^{\circ}$ (green region) and jump to energy band $T_{2}$. It can also absorb the photon of a wavelength $4000A^{\circ}$ (Blue region) and jump to energy band $T_{1}$. The absorption spectrum of chromium ions is shown in the figure below
The chromium ion goes to upper energy state $T_{1}$and $T_{2}$ and stay for $10^{-8} sec $ and then make non radiative transition to metastable states $E_{1}$ and $E_{2}$ respectively which have very log life time $\approx10^{-3}sec$. The number of atoms in these states keeps increasing and at the same time number of atoms in the ground state $E_{1}$ goes on decreasing due to optical pumping. Thus the population inversion is achieved between the metastable state and ground state. At room temperature, if radiation is kept constantly, during the process of pumping, the population at $A_{2}$ level is almost $15%$ more than at level $A_{1}$. Some of the excited atoms in states $E_{3}$ return to ground state $E_{1}$ but with less probability.
When the population inversion is achieved light amplification starts in the resonant cavity. When excited atoms at metastable state $E_{2}$ make transition to ground level $E_{1}$ there are two weak lines at $6943 A^{\circ}$ ($A_{2}$ → $E_{1}$) and $6928 A^{\circ}$ ($A_{1}$ → $E_{1}$) each of width $\approx 6 A^{\circ}$. But Under the lasing condition, the line $6943 A^{\circ}$ dominates over $6928 A^{\circ}$. The emission spectrum of chromium ions in ruby is shown in the figure below:
It shows that pumping transitions are spectrally broad while the emission transition is narrow. The wavelength of two spectral lines $6943 A^{\circ}$ and $6928 A^{\circ}$ are temperature dependent.
- Active Medium
- Resonant Cavity
- Pumping and Cooling Device
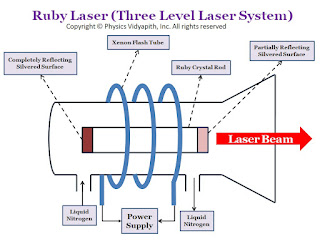 |
| Ruby laser diagram |
 |
| The energy level diagram of chromium ion in ruby |
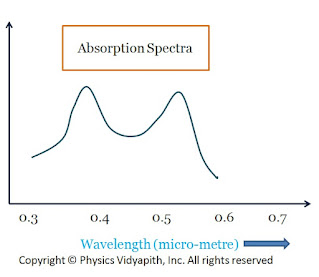 |
| Absorption Spectra |
 |
| Emission Spectra |
Numerical Aperture and Acceptance Angle of the Optical Fibre
Angle of Acceptance →
"If incident angle of light on the core for which the incident angle on the core-cladding interface equals the critical angle then incident angle of light on the core is called the "Angle of Acceptance."
If the incident angle is greater than the acceptance angle i.e. $\theta_{i}>\theta_{0}$ then the angle of incidence on the core-cladding interface will be less than the critical angle due to which part of the incident light is transmitted into cladding as shown in the figure below
If the incident angle is less than the acceptance angle i.e. $\theta_{i}<\theta_{0}$ then the angle of incidence on the core-cladding interface will be greater than the critical angle for which total internal reflection takes place inside the core. As shown in the figure below
Acceptance cone →
"The light entering the core in a cone of semi-vertical angle $\theta_{0}$ is transmitted in the core through total internal reflections. This cone is known as the acceptance cone."
Numerical Aperture→
"The sine of the angle of acceptance of the optical fibre is known as the numerical aperture of optical fibre."
The numerical aperture determines the light-gathering ability of the fibre. It measures the amount of light that can be accepted by a fibre. The numerical aperture depends upon the refractive index of the core and cladding material and does not depend on the physical dimension of the fibre. It is a dimensionless quantity that is less than unity. The value of the numerical aperture ranges from $0.13$ to $0.15$. A large numerical aperture implies that a fibre accepts a large amount of light from the source. It varies due to variations of refractive index in the core and it has zero value after the core-cladding boundary. The number of propagation modes to multimode graded-index fibre depends upon the parameter of numerical aperture and hence upon the relative refractive index difference $\Delta n$
Derivation of Angle of Acceptance and Numerical Aperture →
Let us consider, step-index optical fibre for which
The incident angle on the axis of core = $\theta_{i}$
The refracted angle on the axis of core = $\theta_{r}$
The refractive index of core = $n_{1}$
The refractive index of cladding = $n_{2}$
The incident angle at the core-cladding interface = $\phi$.
When ray incident at point $A$ on the core then According to Snell's law
$\frac{sin \theta_{0}}{sin \theta_{r}}= \frac{n_{1}}{n_{0}} $
Where $n_{0}$ → refractive index of air and vacuum
$sin\theta_{0}=\frac{n_{1}}{n_{0}} sin \theta_{r} \qquad(1)$
Now the refracted ray incident at point $B$ at the interface of core and cladding. So for critical angle condition
$n_{1}\: sin\phi=n_{2} \: sin90^{0} $
From figure: $\phi=90-\theta_{r}$
So above equation can be written as
$n_{1}\: sin(90-\theta_{r})=n_{2} \: sin90^{0}$
$n_{1}\: cos \theta_{r}=n_{2}$
$cos\theta_{r}=\frac{n_{2}}{n_{1}} \qquad(2)$
$sin\theta_{r}=\sqrt{1-cos^{2}\theta_{r}}$
Now substitue the value of $cos\theta_{r}$ from equation$(2)$ to above equation then we get
$sin\theta_{r}=\sqrt{1- \left ( \frac{n_{2}}{n_{1}} \right)^{2}}$
$sin\theta_{r}=\frac{1}{n_{1}}\sqrt{n_{1}^{2}- n_{2}^{2}}$
Now substitue the value of $sin\theta_{r}$ in equation$(1)$ then we get
$sin\theta_{0}=\frac{n_{1}}{n_{0}}\frac{1}{n_{1}}\sqrt{n_{1}^{2}- n_{2}^{2}}$
$sin\theta_{0}=\frac{\sqrt{n_{1}^{2}- n_{2}^{2}}}{n_{0}}\qquad(3)$
This $sin\theta_{0}$ is known as Numerical Aperture. i.e.
$N.A.=\frac{\sqrt{n_{1}^{2}- n_{2}^{2}}}{n_{0}}$
If fibre is in the air then $n_{0}=1$ so the above equation can be written as
$N.A.=\sqrt{n_{1}^{2}- n_{2}^{2}}$
The equation $(3)$ also can be written as
$\theta_{0}=sin^{-1}\frac{\sqrt{n_{1}^{2}- n_{2}^{2}}}{n_{0}}$
The angle $\theta_{0}$ is known as the Angle of Acceptance.
The light is transmitted through the fibre when
$\theta_{i} < \theta_{0}$
i.e. $sin \theta_{i} < sin \theta_{0}$
$sin \theta_{i} < N.A.$
The light will be transmitted through the fibre with multiple total internal reflections when the above condition is satisfied.
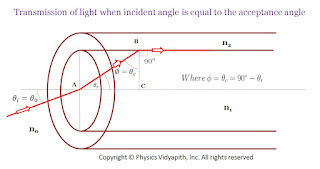 |
| Transmission of light when the incident angle is equal to the acceptance angle |
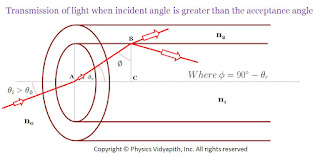 |
| Transmission of light when the incident angle is greater than the acceptance angle |
 |
| Transmission of light when the incident angle is less than the acceptance angle |
The refracted angle on the axis of core = $\theta_{r}$
The refractive index of core = $n_{1}$
The refractive index of cladding = $n_{2}$
The incident angle at the core-cladding interface = $\phi$.
 |
| Transmission of light when the incident angle is equal to the acceptance angle |
Four Level Pumping in Laser
Description:
In four-level pumping, atoms of ground energy state go to upper energy state$(E_{4})$ by pumping transition to achieve the population inversion. Due to the short time of the upper energy state atoms go to metastable state by nonradiative transitions or spontaneous emission. Atoms of metastable state come to lower lasing level by laser transition process. The atoms come from lower lasing level to ground state by nonradiative transition or spontaneous emission. This process is repeated continuously.
In contrast to level pumping, the lower lasing transition level in the four-level scheme is not the ground state and is virtually vacant. As soon as some atoms are pumped to the upper lasing level, population inversion is achieved. So it is required less pumping energy than a three-level laser system. this is the major disadvantage of this scheme. Further, the lifetime of the lower lasing level is shorter as it is not a metastable state. Hence atom in level $E_{2}$ quickly drops to the ground state. This depletion of the $E_{2}$ energy level helps sustain the population inversion by avoiding and accumulation of atoms in the lower lasing level. Therefore four-level laser system can operate in a continuous wave mode.
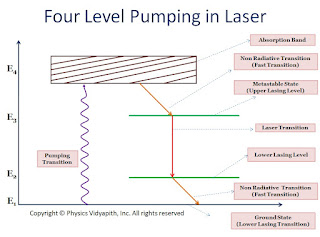 |
| Four-level pumping in Laser |
Three level pumping in Laser
Description:
Three-level pumping in laser is suitable for attending population inversion.
When atoms of ground energy state observe the photon from incident energy. It goes from lower energy or ground energy state two to a higher energy state but the lifetime of a high energy state is very short that is $10^{-8}$ $sec$ i.e. So an atom cannot stay for a long time in high energy state i.e.$E_{3}$ and then the atom goes for non-radiative transition and reach to the metastable state. In a metastable state, Atoms cannot go to a lower energy state or ground energy state directly. Therefore, These atoms come from a metastable state to a lower energy state or ground energy state by lasing transition.
This is the process of three-level pumping in a laser. For better pumping efficiency, The level $E_{3}$ should be the band of energy levels instead of being a single arrow line. It allows the use of pumping radiation of wider bandwidth to excite more atoms. However, the major disadvantage of the three-level scheme is that it requires very high pumping powers. The three-level laser system can produce light only in pulses. Once stimulated emission commences, the metastable state $E_{2}$ gets depopulated very rapidly and the population of the ground energy state increases quickly. As a result, the population inversion ends. One has to wait till population inversion is again established. Thus, the Three-level laser system operates in pulse mode.
 |
| Three-level pumping in Laser |
Two Level Pumping in Laser
Two-level pumping occurs between two energy levels. All the process of laser (absorption, spontaneous emission, or stimulated emission) occurs between two energy level. The absorption of light or emission of light energy is the difference between two energy levels. If two energy levels are $E_{1}$ and $E_{2}$ so absorption or emission of a photon →
Where$h$ → Planck's Constant$\nu$ → Frequency of photon
Two-level pumping in laser is not suitable for attaining the population inversion.
The transition of atoms between two energy levels by stimulated emission is called a lasing transition. The lower level is known as the lower lasing level and the upper level is known as the upper lasing level. The upper lasing level must be a metastable level. The uppermost level to which atoms are in the excited state is known as the pumping level. The transition between the ground level and pumping level is called the pumping transition.
| $E_{2}-E_{1}=h\nu$ |
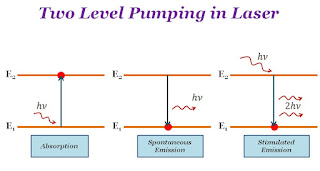 |
| Two-level pumping Laser |
Popular Posts
-
Angle of Acceptance → "If incident angle of light on the core for which the incident angle on the core-cladding interface equals t...
-
Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is ...
-
Maxwell's Equations: Maxwell's equation of the electromagnetic wave is a collection of four equations i.e. Gauss's law of elec...
-
Derivation of interference of light due to a wedge-shaped thin film: Interference of light due to wedge-shaped thin film The wedge...
-
Let a plane wavefront be incident normally on slit $S_{1}$ and $S_{2}$ of equal $e$ and separated by an opaque distance $d$.The diffracted l...
Study-Material
Categories
Alternating Current Circuits
(10)
Atomic and Molecular Physics
(4)
Biomedical
(1)
Capacitors
(6)
Classical Mechanics
(12)
Current carrying loop in magnetic field
(5)
Current Electricity
(10)
Dielectric Materials
(1)
Electromagnetic Induction
(3)
Electromagnetic Wave Theory
(23)
Electrostatic
(22)
Energy Science and Engineering
(2)
Error and Measurement
(2)
Gravitation
(10)
Heat and Thermodynamics
(3)
Kinematics Theory Of Gases
(1)
Laser System & Application
(15)
Magnetic Effect of Current
(9)
Magnetic Substances
(3)
Mechanical Properties of Fluids
(4)
Nanoscience & Nanotechnology
(4)
Nuclear Physics
(7)
Numerical Problems and Solutions
(1)
Optical Fibre
(5)
Optics
(25)
Photoelectric Effect
(3)
Quantum Mechanics
(33)
Relativity
(8)
Semiconductors
(2)
Superconductors
(1)
Topic wise MCQ
(9)
Units and Dimensions
(1)
Waves
(5)





