Basics and types of Nanomaterials

What is a nanoparticle?

Those particles that have size ranges between $1$ to $100 \: nanometres$ are called a nanoparticle. The particles are undetectable by the human eye. There are significant differences in the properties (like magnetic, electrical, Structural, Mechanical, and optical properties) of nanoparticles and bulk materials.

What is nanomaterial?

Those materials that have at least one dimension should be in nanometres i.e. $10^{-9}m$ are called nanomaterials. The prefix 'nano' means a billionth $(10^{-9})$.

Types of nanomaterials

There are two types of nanomaterial that can be classified:

A.) On the basis of dimension

B.) On the basis of material

A.) On the basis of dimensions: According to Siegel, nanostructured materials are classified on the basis of dimension:

1.) Three-dimensional nanomaterials (Bulk Nanomaterial)

2.) Two-dimensional nanomaterials (Quantum Well)

3.) One-dimensional nanomaterials (Quantum Wire)

4.) Zero-dimensional nanomaterials (Quantum Dot)

1.) Three-dimensional nanomaterials (Bulk Nanomaterial): These nanomaterials have not confined to the nanoscale range in any dimension. These materials have three arbitrary dimensions above the nanoscale i.e. $100 nm$. The bulk three-dimensional nanomaterials are composed of a multiple arrangement of nano-size crystals in different orientations. The three-dimensional nanomaterials or bulk nanomaterials can be used as bundles of nanowires, dispersion of nanoparticles, and nanotubes as well as multi-nano layers (polycrystals) in which the $0D$, $1D$, and $2D$ structural elements are in very close contact with each other and form interfaces.

2.) Two-dimensional nanomaterials (Quantum Well): These nanomaterials have one dimension in the nanoscale. It is also called a quantum well. This means that the particles of material are confined only along one dimension. The 2D nanomaterials exhibit plate-like shapes. It includes nanofilms, nanolayers, and nanocoatings with nanometre thickness.

3.) One-dimensional nanomaterials (Quantum Wire): These nanomaterials have two dimensions in the nanoscale. It is also called quantum wire. This means that the particles of material are confined in two dimensions. This leads to needle-shaped nanomaterials. It includes nanofibers, nanotubes, Nanorods, and nanowires.

4.) Zero-dimensional nanomaterials (Quantum Dot): These nanomaterials have all three dimensions in the nanoscale i.e., no dimensions are greater than $100 nm$. It is also called quantum dots. This means that the particles of material are confined in all three dimensions. It includes Nanospheres and nanoclusters.

B.) On the basis of materials: Nanomaterials can be categorized on the basis of material into four types such as:

1.) Inorganic-based nanomaterials (Metal-based materials ):

2.) Carbon-based nanomaterials:

3.) Organic-based nanomaterials (Dendrimers):

4.) Composite-based nanomaterials.

1.) Inorganic-based nanomaterials (Metal-based materials ): Generally, inorganic-based nanomaterials include different metal and metal oxide nanomaterials.

Examples of metal-based inorganic nanomaterials - silver $(Ag)$, gold $(Au)$, aluminum $(Al)$, cadmium $(Cd)$, copper $(Cu)$, iron $(Fe)$, zinc $(Zn)$, and lead $(Pb)$ nanomaterials.

Examples of metal oxide-based inorganic nanomaterials- zinc oxide $(ZnO)$, copper oxide $(CuO)$, magnesium aluminum oxide $(MgAl_{2}O_{4})$, titanium dioxide $(TiO_{2})$, cerium oxide $(CeO_{2})$, iron oxide $(Fe_{2}O_{3})$, silica $(SiO_{2})$, and iron oxide $(Fe_{3}O_{4})$, etc.

(2) Carbon-based nanomaterials: Carbon-based nanomaterials are graphene, fullerene, single-walled carbon nanotube, multi-walled carbon nanotube, carbon fiber, activated carbon, and carbon black.

(3) Organic-based nanomaterials (Dendrimers): The organic-based nanomaterials or dendrimers (i.e. Dendrimers are repetitively branched molecules. Dendrimers name comes from the Greek word ‘dendron’ which means tree.) are formed from organic materials that do not include carbon materials, for instance, dendrimers, cyclodextrin, liposome, and micelle.

(4) Composite-based nanomaterials: The composite nanomaterials can be any combination of all nanomaterials like metal-based, carbon-based, metal oxide-based, and organic-based nanomaterials. These composite nanomaterials have very complicated structures like a metal-organic framework.

Read More

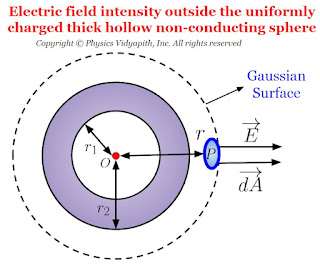
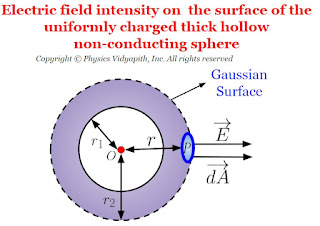
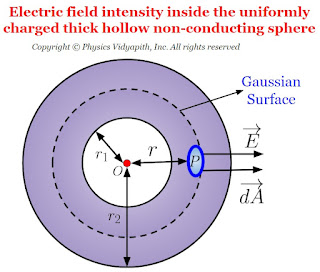
Electric field intensity due to thick hollow non-conducting sphere

Electric field intensity at different points in the field due to uniformly charged thick hollow non-conducting sphere: Let us consider, A hollow non-conducting sphere of inner radius $r_{1}$ and outer radius $r_{2}$ in which $+q$ charge is evenly distributed evenly in the entire volume of the sphere. If $\rho$ is the volume charge density then electric field intensity at different points on the electric field of the thick hollow non-conducting sphere:

1. Electric field intensity outside the thick hollow non-conducting sphere
2. Electric field intensity on the surface of the thick hollow non-conducting sphere
3. Electric field intensity at an internal point of the non-thick hollow conducting sphere

1. Electric field intensity outside the thick hollow non-conducting sphere:

Let us consider, A point $P$ is outside the sphere which is at a $r$ distance from the center point $O$ of the sphere. The direction of electric flux is radially outward in the sphere. So the direction of the electric field vector and the small area vector will be in the same direction i.e. ($\theta =0^{\circ}$). Here $\overrightarrow {dA}$ is a small area element so the small amount of electric flux will pass through this area i.e. →

$ d\phi_{E}= \overrightarrow {E}\cdot \overrightarrow{dA}$

$ d\phi_{E}= E\:dA\: cos\: 0^{\circ} \quad \left \{\because \theta=0^{\circ} \right \}$

$ d\phi_{E}= E\:dA \qquad (1) \quad \left \{\because cos\:0^{\circ}=1 \right \}$

The electric flux passes through the entire Gaussian surface, So integrate the equation $(1)$

$ \oint d\phi_{E}= \oint E\:dA $

$ \phi_{E}=\oint E\:dA\qquad (2)$

According to Gauss's law:

$ \phi_{E}=\frac{q}{\epsilon_{0}}\qquad (3)$

From equation $(2)$ and equation $(3)$, we can write as

$ \frac{q}{\epsilon_{0}}=\oint E\:dA$

$ \frac{q}{\epsilon_{0}}= E\oint dA$

For entire Gaussian spherical surface is

$\oint {dA}=4\pi r^{2}$.

So from the above equations

$ \frac{q}{\epsilon_{0}}= E(4\pi r^{2})$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}} \qquad(4)$

From the above equation, we can conclude that the behavior of the electric field at the external point due to the uniformly charged thick hollow non-conducting sphere is the same as the point charge i.e. like the entire charge is placed at the center.

Since the sphere is a non-conductor so the charge is distributed in the entire volume of the sphere. So charge on the thick hollow sphere-

$q=\frac{4}{3} \pi \left(r_{2}^{3}-r_{1}^{3} \right) \rho $

Substitute this value of charge $q$ in the above equation $(4)$, Therefore,

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{4\pi \left(r_{2}^{3}-r_{1}^{3} \right)\: \rho}{3r^{2}}$

$ E=\frac{\rho}{3 \epsilon_{0}}\frac{\left(r_{2}^{3}-r_{1}^{3} \right)}{r^{2}}$

This equation describes the electric field intensity at the external point of the thick hollow non-conducting sphere.

2. Electric field intensity on the surface of the thick hollow non-conducting sphere:

If point $P$ is placed on the surface of the thick hollow non-conducting sphere i.e. ($r=r_{2}$). so electric field intensity on the surface of the thick hollow non-conducting sphere:

$ E=\frac{\rho}{3\epsilon_{0}}\frac{\left(r^{3}-r_{1}^{3} \right)}{r^{2}}$

3. Electric field intensity at an internal point of the thick hollow non-conducting sphere:

If point $P$ is placed inside the sphere at the distance $r$ from the origin $O$, the electric flux which is passing through the Gaussian surface

$ \phi_{E}= E.4\pi r^{2}$

Where $\phi_{E}=\frac{q'}{\epsilon_{0}}$

$ \frac{q'}{\epsilon_{0}}=E.4\pi r^{2}$

Where $q'$ is part of charge $q$ which is enclosed with Gaussian Surface

$ E=\frac{1}{4 \pi \epsilon_{0}} \frac{q'}{r^{2}} \qquad \qquad (5)$

The charge is distributed uniformly in the entire volume of the sphere so volume charge density $\rho$ will be the same as the entire sphere i.e.

$ \rho=\frac{q}{\frac{4}{3}\pi \left(r_{2}^{3}-r_{1}^{3} \right)}=\frac{q'}{\frac{4}{3}\pi \left(r^{3}-r_{1}^{3} \right)}$

$ \frac{q}{\left(r_{2}^{3}-r_{1}^{3} \right)}=\frac{q'}{\left(r^{3}-r_{1}^{3} \right)}$

$ q'=q\frac{\left(r^{3}-r_{1}^{3} \right) }{\left(r_{2}^{3}-r_{1}^{3} \right)}$

Put the value of $q'$ in equation $(5)$, so

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q} {r^{2}} \frac{\left(r^{3}-r_{1}^{3} \right) }{\left(r_{2}^{3}-r_{1}^{3} \right)}$

Where $q=\frac{4}{3} \pi \left(r_{2}^{3}-r_{1}^{3} \right) \rho $. So above equation can be written as:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{\frac{4}{3} \pi \left(r_{2}^{3}-r_{1}^{3} \right) \rho } {r^{2}} \frac{\left(r^{3}-r_{1}^{3} \right) }{\left(r_{2}^{3}-r_{1}^{3} \right)}$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{\frac{4}{3} \pi \left(r_{2}^{3}-r_{1}^{3} \right) \rho } {r^{2}} \frac{\left(r^{3}-r_{1}^{3} \right) }{\left(r_{2}^{3}-r_{1}^{3} \right)}$

$E=\frac{ \rho }{3 \epsilon_{0}} \frac{\left(r^{3}-r_{1}^{3} \right)}{r^{2}}$

Read More

Characteristics of Electromagnetic Wave

Electromagnetic Wave:

An electromagnetic wave is the combined effect of an electric field and magnetic field which carry energy from one place to another.

When an electric field and the magnetic field are applied perpendicular to each other then a wave propagates perpendicular to both the electric field and the magnetic field. This wave is called the electromagnetic wave.

Characteristics of Electromagnetic Wave:

1.) Electric and Magnetic Fields: Electromagnetic waves are produced through the mutually perpendicular interaction of electric and magnetic fields. The propagation of the wave is also perpendicular to both the electric field and the magnetic field.

2.) Wave Nature of electromagnetic waves: Electromagnetic waves are characterized by their wave-like behavior, so they exhibit the properties such as wavelength, frequency, amplitude, and velocity. This wave-like behavior of electromagnetic waves can undergo phenomena like interference, diffraction, and polarization.

3.) The spectrum of an electromagnetic wave: In the spectrum of electromagnetic waves, All the wavelengths and frequencies of the waves are included such as radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays etc.

4.) Speed of electromagnetic wave: The speed of electromagnetic waves in free space or vacuum is equal to the speed of light in free space or vacuum, which is approximately 299,792 $Km/s$.

5.) Transverse waves of an electromagnetic wave: Electromagnetic waves are transverse waves which mean that the oscillations of the electric and magnetic fields occur perpendicular to the direction of wave propagation.

6.) Dual nature of electromagnetic wave: Electromagnetic waves have both wave-like and particle-like behavior. They can be described as a stream of particles called photons, each photon carrying a specific amount of energy (quantum). This duality is described by the wave-particle duality principle in quantum mechanics.

7.) Energy transfer in electromagnetic waves: Electromagnetic waves transport energy through space. The amount of energy carried by each wave depends on its frequency. Higher frequency waves, such as gamma rays and X-rays, carry more energy than lower frequency waves like radio waves.

8.) Absorption, Reflection, and Transmission of Electromagnetic waves: Electromagnetic waves can be absorbed by certain materials, reflected off surfaces, or transmitted through transparent substances. The behavior of waves at boundaries depends on factors such as the angle of incidence, the nature of the material, and the frequency of the wave.

9.) Electromagnetic Induction of electromagnetic wave: When electromagnetic waves interact with conductive materials or circuits, they can induce electric currents or voltages. This principle is the basis for technologies like antennas, wireless communication, and electromagnetic sensors.

10.) Electromagnetic Interactions of electromagnetic waves: Electromagnetic waves can interact with matter in various ways, including absorption, scattering, and emission. These interactions are utilized in fields such as optics, spectroscopy, medical imaging, and telecommunications.

Read More

Electric and magnetic field vector are mutually perpendicular to each other in electromagnetic wave

In electromagnetic waves, the electric field vector and magnetic field vector are mutually perpendicular to each other (Proof)

The general solution of the wave equation for the electric field vector and magnetic field vector are respectively given below

$\overrightarrow{E}= E_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \qquad(1)$

$\overrightarrow{B}= B_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \qquad(2)$

Here $E_{\circ}$ and $B_{\circ}$ are the complex amplitude of electric field vector $\overrightarrow{E}$ and magnetic field vector $\overrightarrow{B}$ respectively and $\overrightarrow{k}$ is the propagation constant.

Now

$\overrightarrow{\nabla} \times \overrightarrow{E}= \left( \hat{i} \frac{\partial}{\partial x} + \hat{i} \frac{\partial}{\partial x} +\hat{i} \frac{\partial}{\partial x} \right). \left( \hat{i}E_{x} + \hat{j}E_{y} + \hat{k}E_{z} \right) $

$\overrightarrow{\nabla} \times \overrightarrow{E} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ E_{x} & E_{y} & E_{z} \\ \end{vmatrix}$

$\overrightarrow{\nabla} \times \overrightarrow{E} = \hat{i} \left[ \frac{\partial E_{z}}{\partial y} -\frac{\partial E_{y}}{\partial z} \right] - \hat{j} \left[ \frac{\partial E_{z}}{\partial x} -\frac{\partial E_{x}}{\partial z} \right] + \hat{k} \left[ \frac{\partial E_{y}}{\partial x} -\frac{\partial E_{x}}{\partial y } \right] \qquad(3)$

Here $E_{x}$, $E_{y}$ and $E_{z}$ are the component of electric field vector $\overrightarrow{E}$ in $x$, $y$, and $z$ direction. So the component form of the equation $(1)$

$\overrightarrow{E_{x}}= E_{\circ x} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

$\overrightarrow{E_{y}}= E_{\circ y} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

$\overrightarrow{E_{z}}= E_{\circ z} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

We know that:

$\overrightarrow{k}.\overrightarrow{r}=\left( \hat{i}k_{x} + \hat{j}k_{y} + \hat{k}k_{z} \right). \left( \hat{i}x + \hat{j}y +\hat{k}z \right)$

$\overrightarrow{k}.\overrightarrow{r}=x k_{x} + yk_{y} + zk_{z} $

So above equation can be written as:

$\overrightarrow{E_{x}}= E_{\circ x} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \qquad(4)$

$\overrightarrow{E_{y}}= E_{\circ y} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \qquad(5)$

$\overrightarrow{E_{z}}= E_{\circ z} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \qquad(6)$

Now find that derivative from the equation $(4)$, equation $(5)$, and equation $(6)$ then substitute these values in equation $(3)$, So we get

$\left[ \frac{\partial E_{z}}{\partial y} -\frac{\partial E_{y}}{\partial z} \right] = \frac{\partial E_{z}}{\partial y} - \frac{\partial E_{y}}{\partial z} $

$\left[ \frac{\partial E_{z}}{\partial y} -\frac{\partial E_{y}}{\partial z} \right] = \frac{\partial}{\partial y} \left( E_{\circ z} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \right) -\frac{\partial}{\partial z} \left( E_{\circ y} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \right) $

$\left[ \frac{\partial E_{z}}{\partial y} -\frac{\partial E_{y}}{\partial z} \right] = \left(i k_{y} E_{z} - i k_{z} E_{y} \right) $

$\left[ \frac{\partial E_{z}}{\partial y} -\frac{\partial E_{y}}{\partial z} \right] = i \left( k_{y} E_{z} - k_{z} E_{y} \right) \qquad(7)$

Similarly

$\left[ \frac{\partial E_{z}}{\partial x} -\frac{\partial E_{x}}{\partial z} \right] = i \left( k_{x} E_{z} - k_{z} E_{x} \right) \qquad(8)$

$\left[ \frac{\partial E_{y}}{\partial x} -\frac{\partial E_{x}}{\partial y} \right] = i \left( k_{x} E_{y} - k_{y} E_{x} \right) \qquad(9)$

Now substitute the value of equation $(7)$, equation $(8)$, and equation $(9)$ in equation $(3)$

$\overrightarrow{\nabla} \times \overrightarrow{E} = i \left[\hat{i} \left( k_{y} E_{z} - k_{z} E_{y} \right) - \hat{j} \left( k_{x} E_{z} - k_{z} E_{x} \right) _ \hat{k} \left( k_{x} E_{y} - k_{y} E_{x} \right) \right]$

$\overrightarrow{\nabla} \times \overrightarrow{E} = i \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ k_{x} & k_{y} & k_{z} \\ E_{x} & E_{y} & E_{z} \\ \end{vmatrix}$

$\overrightarrow{\nabla} \times \overrightarrow{E} = i \left( \overrightarrow{k} \times \overrightarrow{E} \right) \qquad(10)$

According to Maxwell's third equation

$\overrightarrow{\nabla} \times \overrightarrow{E}= - \frac{\partial \overrightarrow{B}}{\partial t}$

$\overrightarrow{\nabla} \times \overrightarrow{E}= - \frac{\partial}{\partial t} \left( B_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \right) \quad \left\{From \: equation \: (2)\right\}$

$\overrightarrow{\nabla} \times \overrightarrow{E}= i \omega \overrightarrow{B} \qquad(11)$

From equation $(10)$ and equation $(11)$

$i \left( \overrightarrow{k} \times \overrightarrow{E} \right) = i \omega \overrightarrow{B}$

$ \left( \overrightarrow{k} \times \overrightarrow{E} \right) = \omega \overrightarrow{B} \qquad(12)$

$\therefore$ Magnetic field vector $(\overrightarrow{B})$ is perpendicular to both electric field vector $(\overrightarrow{E})$ and propagation of wave vector $(\overrightarrow{k})$.

Similarly, from $\overrightarrow{\nabla} \times \overrightarrow{B}$, we get

$ \left( \overrightarrow{k} \times \overrightarrow{B} \right) = -\frac{\omega}{c} \overrightarrow{E} \qquad(13)$

Thus, In an electromagnetic wave, the electric field and magnetic field vector are perpendicular to each other and also to the direction of propagation of the wave.

Read More

Transverse Nature of Electromagnetic Wave

Electromagnetic waves are transverse in nature: (Proof)

The general solution of the wave equation for the electric field and magnetic field are respectively given below

$\overrightarrow{E}= E_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \qquad(1)$

$\overrightarrow{B}= B_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \qquad(2)$

Here $E_{\circ}$ and $B_{\circ}$ are the complex amplitude of electric field vector $\overrightarrow{E}$ and magnetic field vector $\overrightarrow{B}$ respectively and $\overrightarrow{k}$ is the propagation constant.

Now

$\overrightarrow{\nabla}. \overrightarrow{E}= \left( \hat{i} \frac{\partial}{\partial x} + \hat{i} \frac{\partial}{\partial x} +\hat{i} \frac{\partial}{\partial x} \right). \left( \hat{i}E_{x} + \hat{j}E_{y} + \hat{k}E_{z} \right) $

$\overrightarrow{\nabla}. \overrightarrow{E}= \frac{\partial}{\partial x} \left(E_{x} \right)+ \frac{\partial}{\partial y} \left(E_{y} \right) + \frac{\partial}{\partial z} \left(E_{z} \right) \qquad(3)$

Here $E_{x}$, $E_{y}$ and $E_{z}$ are the component of electric field $\overrightarrow{E}$ in $x$, $y$, and $z$ direction. So the component form of the equation $(1)$

$\overrightarrow{E_{x}}= E_{\circ x} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

$\overrightarrow{E_{y}}= E_{\circ y} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

$\overrightarrow{E_{z}}= E_{\circ z} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

Here

$\overrightarrow{k}.\overrightarrow{r}=\left( \hat{i}k_{x} + \hat{j}k_{y} + \hat{k}k_{z} \right). \left( \hat{i}x + \hat{j}y +\hat{k}z \right)$

$\overrightarrow{k}.\overrightarrow{r}=x k_{x} + yk_{y} + zk_{z} $

So above equation can be written as:

$\overrightarrow{E_{x}}= E_{\circ x} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \qquad(4)$

$\overrightarrow{E_{y}}= E_{\circ y} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \qquad(5)$

$\overrightarrow{E_{z}}= E_{\circ z} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \qquad(6)$

Now find that derivative of the equation $(4)$ along the direction of $x$ then

$\frac{\partial E_{x}}{\partial x} = i k_{x} E_{\circ x} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} $

$\frac{\partial E_{x}}{\partial x} = i k_{x} E_{x} $

Similarly, the derivative of the equation $(5)$, and equation $(6)$ along the direction of $y$ and $z$ then

$\frac{\partial E_{y}}{\partial y} = i k_{y} E_{y} $

$\frac{\partial E_{z}}{\partial z} = i k_{z} E_{z} $

Now substitute the value of $\frac{\partial E_{x}}{\partial x}$, $\frac{\partial E_{y}}{\partial y}$, and $\frac{\partial E_{z}}{\partial z}$ in equation $(3)$

$\overrightarrow{\nabla}. \overrightarrow{E}= i k_{x} E_{x} + i k_{y} E_{y} + i k_{z} E_{z}$

$\overrightarrow{\nabla}. \overrightarrow{E}= i \left( k_{x} E_{x} + k_{y} E_{y} + k_{z} E_{z} \right)$

$\overrightarrow{\nabla}. \overrightarrow{E}= i \left( \hat{i}k_{x} + \hat{j}k_{y} + \hat{k}k_{z} \right). \left( \hat{i}E_{x} + \hat{j}E_{y} + \hat{k} E_{z} \right)$

$\overrightarrow{\nabla}. \overrightarrow{E}= i \left( \overrightarrow {k} . \overrightarrow {E} \right) \qquad(7)$

From Maxwell's first equation in free space:

$\overrightarrow{\nabla}. \overrightarrow{E}= 0 \qquad(8)$

From equation $(7)$ and equation $(8)$

$i \left( \overrightarrow {k} . \overrightarrow {E} \right)=0$

$ \overrightarrow {k} . \overrightarrow {E} = 0$

From the above equation, we can conclude that the electric field is perpendicular to the direction of propagation of the wave i.e. $\overrightarrow {E}\perp \overrightarrow {k}$

Similarly, The same result is obtained from $\overrightarrow{\nabla}. \overrightarrow {B}$ i.e. $ \overrightarrow {k} . \overrightarrow {B} = 0$, So we can conclude that the magnetic field is also perpendicular to the direction of propagation i.e. $\overrightarrow {B}\perp \overrightarrow {k}$

Thus, "The electromagnetic waves are transverse in nature"

Read More