Basics and types of Nanomaterials

What is a nanoparticle?

Those particles that have size ranges between $1$ to $100 \: nanometres$ are called a nanoparticle. The particles are undetectable by the human eye. There are significant differences in the properties (like magnetic, electrical, Structural, Mechanical, and optical properties) of nanoparticles and bulk materials.

What is nanomaterial?

Those materials that have at least one dimension should be in nanometres i.e. $10^{-9}m$ are called nanomaterials. The prefix 'nano' means a billionth $(10^{-9})$.

Types of nanomaterials

There are two types of nanomaterial that can be classified:

A.) On the basis of dimension

B.) On the basis of material

A.) On the basis of dimensions: According to Siegel, nanostructured materials are classified on the basis of dimension:

1.) Three-dimensional nanomaterials (Bulk Nanomaterial)

2.) Two-dimensional nanomaterials (Quantum Well)

3.) One-dimensional nanomaterials (Quantum Wire)

4.) Zero-dimensional nanomaterials (Quantum Dot)

1.) Three-dimensional nanomaterials (Bulk Nanomaterial): These nanomaterials have not confined to the nanoscale range in any dimension. These materials have three arbitrary dimensions above the nanoscale i.e. $100 nm$. The bulk three-dimensional nanomaterials are composed of a multiple arrangement of nano-size crystals in different orientations. The three-dimensional nanomaterials or bulk nanomaterials can be used as bundles of nanowires, dispersion of nanoparticles, and nanotubes as well as multi-nano layers (polycrystals) in which the $0D$, $1D$, and $2D$ structural elements are in very close contact with each other and form interfaces.

2.) Two-dimensional nanomaterials (Quantum Well): These nanomaterials have one dimension in the nanoscale. It is also called a quantum well. This means that the particles of material are confined only along one dimension. The 2D nanomaterials exhibit plate-like shapes. It includes nanofilms, nanolayers, and nanocoatings with nanometre thickness.

3.) One-dimensional nanomaterials (Quantum Wire): These nanomaterials have two dimensions in the nanoscale. It is also called quantum wire. This means that the particles of material are confined in two dimensions. This leads to needle-shaped nanomaterials. It includes nanofibers, nanotubes, Nanorods, and nanowires.

4.) Zero-dimensional nanomaterials (Quantum Dot): These nanomaterials have all three dimensions in the nanoscale i.e., no dimensions are greater than $100 nm$. It is also called quantum dots. This means that the particles of material are confined in all three dimensions. It includes Nanospheres and nanoclusters.

B.) On the basis of materials: Nanomaterials can be categorized on the basis of material into four types such as:

1.) Inorganic-based nanomaterials (Metal-based materials ):

2.) Carbon-based nanomaterials:

3.) Organic-based nanomaterials (Dendrimers):

4.) Composite-based nanomaterials.

1.) Inorganic-based nanomaterials (Metal-based materials ): Generally, inorganic-based nanomaterials include different metal and metal oxide nanomaterials.

Examples of metal-based inorganic nanomaterials - silver $(Ag)$, gold $(Au)$, aluminum $(Al)$, cadmium $(Cd)$, copper $(Cu)$, iron $(Fe)$, zinc $(Zn)$, and lead $(Pb)$ nanomaterials.

Examples of metal oxide-based inorganic nanomaterials- zinc oxide $(ZnO)$, copper oxide $(CuO)$, magnesium aluminum oxide $(MgAl_{2}O_{4})$, titanium dioxide $(TiO_{2})$, cerium oxide $(CeO_{2})$, iron oxide $(Fe_{2}O_{3})$, silica $(SiO_{2})$, and iron oxide $(Fe_{3}O_{4})$, etc.

(2) Carbon-based nanomaterials: Carbon-based nanomaterials are graphene, fullerene, single-walled carbon nanotube, multi-walled carbon nanotube, carbon fiber, activated carbon, and carbon black.

(3) Organic-based nanomaterials (Dendrimers): The organic-based nanomaterials or dendrimers (i.e. Dendrimers are repetitively branched molecules. Dendrimers name comes from the Greek word ‘dendron’ which means tree.) are formed from organic materials that do not include carbon materials, for instance, dendrimers, cyclodextrin, liposome, and micelle.

(4) Composite-based nanomaterials: The composite nanomaterials can be any combination of all nanomaterials like metal-based, carbon-based, metal oxide-based, and organic-based nanomaterials. These composite nanomaterials have very complicated structures like a metal-organic framework.

Read More

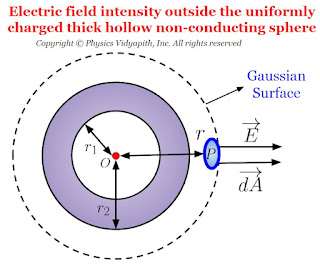
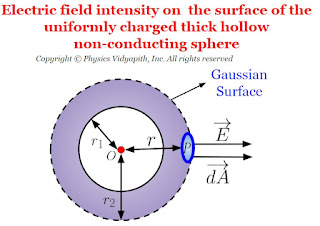
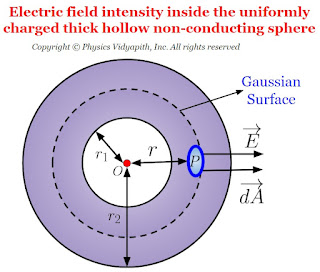
Electric field intensity due to thick hollow non-conducting sphere

Electric field intensity at different points in the field due to uniformly charged thick hollow non-conducting sphere: Let us consider, A hollow non-conducting sphere of inner radius $r_{1}$ and outer radius $r_{2}$ in which $+q$ charge is evenly distributed evenly in the entire volume of the sphere. If $\rho$ is the volume charge density then electric field intensity at different points on the electric field of the thick hollow non-conducting sphere:

1. Electric field intensity outside the thick hollow non-conducting sphere
2. Electric field intensity on the surface of the thick hollow non-conducting sphere
3. Electric field intensity at an internal point of the non-thick hollow conducting sphere

1. Electric field intensity outside the thick hollow non-conducting sphere:

Let us consider, A point $P$ is outside the sphere which is at a $r$ distance from the center point $O$ of the sphere. The direction of electric flux is radially outward in the sphere. So the direction of the electric field vector and the small area vector will be in the same direction i.e. ($\theta =0^{\circ}$). Here $\overrightarrow {dA}$ is a small area element so the small amount of electric flux will pass through this area i.e. →

$ d\phi_{E}= \overrightarrow {E}\cdot \overrightarrow{dA}$

$ d\phi_{E}= E\:dA\: cos\: 0^{\circ} \quad \left \{\because \theta=0^{\circ} \right \}$

$ d\phi_{E}= E\:dA \qquad (1) \quad \left \{\because cos\:0^{\circ}=1 \right \}$

The electric flux passes through the entire Gaussian surface, So integrate the equation $(1)$

$ \oint d\phi_{E}= \oint E\:dA $

$ \phi_{E}=\oint E\:dA\qquad (2)$

According to Gauss's law:

$ \phi_{E}=\frac{q}{\epsilon_{0}}\qquad (3)$

From equation $(2)$ and equation $(3)$, we can write as

$ \frac{q}{\epsilon_{0}}=\oint E\:dA$

$ \frac{q}{\epsilon_{0}}= E\oint dA$

For entire Gaussian spherical surface is

$\oint {dA}=4\pi r^{2}$.

So from the above equations

$ \frac{q}{\epsilon_{0}}= E(4\pi r^{2})$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}} \qquad(4)$

From the above equation, we can conclude that the behavior of the electric field at the external point due to the uniformly charged thick hollow non-conducting sphere is the same as the point charge i.e. like the entire charge is placed at the center.

Since the sphere is a non-conductor so the charge is distributed in the entire volume of the sphere. So charge on the thick hollow sphere-

$q=\frac{4}{3} \pi \left(r_{2}^{3}-r_{1}^{3} \right) \rho $

Substitute this value of charge $q$ in the above equation $(4)$, Therefore,

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{4\pi \left(r_{2}^{3}-r_{1}^{3} \right)\: \rho}{3r^{2}}$

$ E=\frac{\rho}{3 \epsilon_{0}}\frac{\left(r_{2}^{3}-r_{1}^{3} \right)}{r^{2}}$

This equation describes the electric field intensity at the external point of the thick hollow non-conducting sphere.

2. Electric field intensity on the surface of the thick hollow non-conducting sphere:

If point $P$ is placed on the surface of the thick hollow non-conducting sphere i.e. ($r=r_{2}$). so electric field intensity on the surface of the thick hollow non-conducting sphere:

$ E=\frac{\rho}{3\epsilon_{0}}\frac{\left(r^{3}-r_{1}^{3} \right)}{r^{2}}$

3. Electric field intensity at an internal point of the thick hollow non-conducting sphere:

If point $P$ is placed inside the sphere at the distance $r$ from the origin $O$, the electric flux which is passing through the Gaussian surface

$ \phi_{E}= E.4\pi r^{2}$

Where $\phi_{E}=\frac{q'}{\epsilon_{0}}$

$ \frac{q'}{\epsilon_{0}}=E.4\pi r^{2}$

Where $q'$ is part of charge $q$ which is enclosed with Gaussian Surface

$ E=\frac{1}{4 \pi \epsilon_{0}} \frac{q'}{r^{2}} \qquad \qquad (5)$

The charge is distributed uniformly in the entire volume of the sphere so volume charge density $\rho$ will be the same as the entire sphere i.e.

$ \rho=\frac{q}{\frac{4}{3}\pi \left(r_{2}^{3}-r_{1}^{3} \right)}=\frac{q'}{\frac{4}{3}\pi \left(r^{3}-r_{1}^{3} \right)}$

$ \frac{q}{\left(r_{2}^{3}-r_{1}^{3} \right)}=\frac{q'}{\left(r^{3}-r_{1}^{3} \right)}$

$ q'=q\frac{\left(r^{3}-r_{1}^{3} \right) }{\left(r_{2}^{3}-r_{1}^{3} \right)}$

Put the value of $q'$ in equation $(5)$, so

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q} {r^{2}} \frac{\left(r^{3}-r_{1}^{3} \right) }{\left(r_{2}^{3}-r_{1}^{3} \right)}$

Where $q=\frac{4}{3} \pi \left(r_{2}^{3}-r_{1}^{3} \right) \rho $. So above equation can be written as:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{\frac{4}{3} \pi \left(r_{2}^{3}-r_{1}^{3} \right) \rho } {r^{2}} \frac{\left(r^{3}-r_{1}^{3} \right) }{\left(r_{2}^{3}-r_{1}^{3} \right)}$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{\frac{4}{3} \pi \left(r_{2}^{3}-r_{1}^{3} \right) \rho } {r^{2}} \frac{\left(r^{3}-r_{1}^{3} \right) }{\left(r_{2}^{3}-r_{1}^{3} \right)}$

$E=\frac{ \rho }{3 \epsilon_{0}} \frac{\left(r^{3}-r_{1}^{3} \right)}{r^{2}}$

Read More

Characteristics of Electromagnetic Wave

Electromagnetic Wave:

An electromagnetic wave is the combined effect of an electric field and magnetic field which carry energy from one place to another.

When an electric field and the magnetic field are applied perpendicular to each other then a wave propagates perpendicular to both the electric field and the magnetic field. This wave is called the electromagnetic wave.

Characteristics of Electromagnetic Wave:

1.) Electric and Magnetic Fields: Electromagnetic waves are produced through the mutually perpendicular interaction of electric and magnetic fields. The propagation of the wave is also perpendicular to both the electric field and the magnetic field.

2.) Wave Nature of electromagnetic waves: Electromagnetic waves are characterized by their wave-like behavior, so they exhibit the properties such as wavelength, frequency, amplitude, and velocity. This wave-like behavior of electromagnetic waves can undergo phenomena like interference, diffraction, and polarization.

3.) The spectrum of an electromagnetic wave: In the spectrum of electromagnetic waves, All the wavelengths and frequencies of the waves are included such as radio waves, microwaves, infrared, visible light, ultraviolet, X-rays, and gamma rays etc.

4.) Speed of electromagnetic wave: The speed of electromagnetic waves in free space or vacuum is equal to the speed of light in free space or vacuum, which is approximately 299,792 $Km/s$.

5.) Transverse waves of an electromagnetic wave: Electromagnetic waves are transverse waves which mean that the oscillations of the electric and magnetic fields occur perpendicular to the direction of wave propagation.

6.) Dual nature of electromagnetic wave: Electromagnetic waves have both wave-like and particle-like behavior. They can be described as a stream of particles called photons, each photon carrying a specific amount of energy (quantum). This duality is described by the wave-particle duality principle in quantum mechanics.

7.) Energy transfer in electromagnetic waves: Electromagnetic waves transport energy through space. The amount of energy carried by each wave depends on its frequency. Higher frequency waves, such as gamma rays and X-rays, carry more energy than lower frequency waves like radio waves.

8.) Absorption, Reflection, and Transmission of Electromagnetic waves: Electromagnetic waves can be absorbed by certain materials, reflected off surfaces, or transmitted through transparent substances. The behavior of waves at boundaries depends on factors such as the angle of incidence, the nature of the material, and the frequency of the wave.

9.) Electromagnetic Induction of electromagnetic wave: When electromagnetic waves interact with conductive materials or circuits, they can induce electric currents or voltages. This principle is the basis for technologies like antennas, wireless communication, and electromagnetic sensors.

10.) Electromagnetic Interactions of electromagnetic waves: Electromagnetic waves can interact with matter in various ways, including absorption, scattering, and emission. These interactions are utilized in fields such as optics, spectroscopy, medical imaging, and telecommunications.

Read More

Electric and magnetic field vector are mutually perpendicular to each other in electromagnetic wave

In electromagnetic waves, the electric field vector and magnetic field vector are mutually perpendicular to each other (Proof)

The general solution of the wave equation for the electric field vector and magnetic field vector are respectively given below

$\overrightarrow{E}= E_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \qquad(1)$

$\overrightarrow{B}= B_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \qquad(2)$

Here $E_{\circ}$ and $B_{\circ}$ are the complex amplitude of electric field vector $\overrightarrow{E}$ and magnetic field vector $\overrightarrow{B}$ respectively and $\overrightarrow{k}$ is the propagation constant.

Now

$\overrightarrow{\nabla} \times \overrightarrow{E}= \left( \hat{i} \frac{\partial}{\partial x} + \hat{i} \frac{\partial}{\partial x} +\hat{i} \frac{\partial}{\partial x} \right). \left( \hat{i}E_{x} + \hat{j}E_{y} + \hat{k}E_{z} \right) $

$\overrightarrow{\nabla} \times \overrightarrow{E} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ E_{x} & E_{y} & E_{z} \\ \end{vmatrix}$

$\overrightarrow{\nabla} \times \overrightarrow{E} = \hat{i} \left[ \frac{\partial E_{z}}{\partial y} -\frac{\partial E_{y}}{\partial z} \right] - \hat{j} \left[ \frac{\partial E_{z}}{\partial x} -\frac{\partial E_{x}}{\partial z} \right] + \hat{k} \left[ \frac{\partial E_{y}}{\partial x} -\frac{\partial E_{x}}{\partial y } \right] \qquad(3)$

Here $E_{x}$, $E_{y}$ and $E_{z}$ are the component of electric field vector $\overrightarrow{E}$ in $x$, $y$, and $z$ direction. So the component form of the equation $(1)$

$\overrightarrow{E_{x}}= E_{\circ x} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

$\overrightarrow{E_{y}}= E_{\circ y} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

$\overrightarrow{E_{z}}= E_{\circ z} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

We know that:

$\overrightarrow{k}.\overrightarrow{r}=\left( \hat{i}k_{x} + \hat{j}k_{y} + \hat{k}k_{z} \right). \left( \hat{i}x + \hat{j}y +\hat{k}z \right)$

$\overrightarrow{k}.\overrightarrow{r}=x k_{x} + yk_{y} + zk_{z} $

So above equation can be written as:

$\overrightarrow{E_{x}}= E_{\circ x} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \qquad(4)$

$\overrightarrow{E_{y}}= E_{\circ y} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \qquad(5)$

$\overrightarrow{E_{z}}= E_{\circ z} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \qquad(6)$

Now find that derivative from the equation $(4)$, equation $(5)$, and equation $(6)$ then substitute these values in equation $(3)$, So we get

$\left[ \frac{\partial E_{z}}{\partial y} -\frac{\partial E_{y}}{\partial z} \right] = \frac{\partial E_{z}}{\partial y} - \frac{\partial E_{y}}{\partial z} $

$\left[ \frac{\partial E_{z}}{\partial y} -\frac{\partial E_{y}}{\partial z} \right] = \frac{\partial}{\partial y} \left( E_{\circ z} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \right) -\frac{\partial}{\partial z} \left( E_{\circ y} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \right) $

$\left[ \frac{\partial E_{z}}{\partial y} -\frac{\partial E_{y}}{\partial z} \right] = \left(i k_{y} E_{z} - i k_{z} E_{y} \right) $

$\left[ \frac{\partial E_{z}}{\partial y} -\frac{\partial E_{y}}{\partial z} \right] = i \left( k_{y} E_{z} - k_{z} E_{y} \right) \qquad(7)$

Similarly

$\left[ \frac{\partial E_{z}}{\partial x} -\frac{\partial E_{x}}{\partial z} \right] = i \left( k_{x} E_{z} - k_{z} E_{x} \right) \qquad(8)$

$\left[ \frac{\partial E_{y}}{\partial x} -\frac{\partial E_{x}}{\partial y} \right] = i \left( k_{x} E_{y} - k_{y} E_{x} \right) \qquad(9)$

Now substitute the value of equation $(7)$, equation $(8)$, and equation $(9)$ in equation $(3)$

$\overrightarrow{\nabla} \times \overrightarrow{E} = i \left[\hat{i} \left( k_{y} E_{z} - k_{z} E_{y} \right) - \hat{j} \left( k_{x} E_{z} - k_{z} E_{x} \right) _ \hat{k} \left( k_{x} E_{y} - k_{y} E_{x} \right) \right]$

$\overrightarrow{\nabla} \times \overrightarrow{E} = i \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ k_{x} & k_{y} & k_{z} \\ E_{x} & E_{y} & E_{z} \\ \end{vmatrix}$

$\overrightarrow{\nabla} \times \overrightarrow{E} = i \left( \overrightarrow{k} \times \overrightarrow{E} \right) \qquad(10)$

According to Maxwell's third equation

$\overrightarrow{\nabla} \times \overrightarrow{E}= - \frac{\partial \overrightarrow{B}}{\partial t}$

$\overrightarrow{\nabla} \times \overrightarrow{E}= - \frac{\partial}{\partial t} \left( B_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \right) \quad \left\{From \: equation \: (2)\right\}$

$\overrightarrow{\nabla} \times \overrightarrow{E}= i \omega \overrightarrow{B} \qquad(11)$

From equation $(10)$ and equation $(11)$

$i \left( \overrightarrow{k} \times \overrightarrow{E} \right) = i \omega \overrightarrow{B}$

$ \left( \overrightarrow{k} \times \overrightarrow{E} \right) = \omega \overrightarrow{B} \qquad(12)$

$\therefore$ Magnetic field vector $(\overrightarrow{B})$ is perpendicular to both electric field vector $(\overrightarrow{E})$ and propagation of wave vector $(\overrightarrow{k})$.

Similarly, from $\overrightarrow{\nabla} \times \overrightarrow{B}$, we get

$ \left( \overrightarrow{k} \times \overrightarrow{B} \right) = -\frac{\omega}{c} \overrightarrow{E} \qquad(13)$

Thus, In an electromagnetic wave, the electric field and magnetic field vector are perpendicular to each other and also to the direction of propagation of the wave.

Read More

Transverse Nature of Electromagnetic Wave

Electromagnetic waves are transverse in nature: (Proof)

The general solution of the wave equation for the electric field and magnetic field are respectively given below

$\overrightarrow{E}= E_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \qquad(1)$

$\overrightarrow{B}= B_{\circ} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)} \qquad(2)$

Here $E_{\circ}$ and $B_{\circ}$ are the complex amplitude of electric field vector $\overrightarrow{E}$ and magnetic field vector $\overrightarrow{B}$ respectively and $\overrightarrow{k}$ is the propagation constant.

Now

$\overrightarrow{\nabla}. \overrightarrow{E}= \left( \hat{i} \frac{\partial}{\partial x} + \hat{i} \frac{\partial}{\partial x} +\hat{i} \frac{\partial}{\partial x} \right). \left( \hat{i}E_{x} + \hat{j}E_{y} + \hat{k}E_{z} \right) $

$\overrightarrow{\nabla}. \overrightarrow{E}= \frac{\partial}{\partial x} \left(E_{x} \right)+ \frac{\partial}{\partial y} \left(E_{y} \right) + \frac{\partial}{\partial z} \left(E_{z} \right) \qquad(3)$

Here $E_{x}$, $E_{y}$ and $E_{z}$ are the component of electric field $\overrightarrow{E}$ in $x$, $y$, and $z$ direction. So the component form of the equation $(1)$

$\overrightarrow{E_{x}}= E_{\circ x} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

$\overrightarrow{E_{y}}= E_{\circ y} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

$\overrightarrow{E_{z}}= E_{\circ z} e^{i(\overrightarrow{k}. \overrightarrow{r} - \omega t)}$

Here

$\overrightarrow{k}.\overrightarrow{r}=\left( \hat{i}k_{x} + \hat{j}k_{y} + \hat{k}k_{z} \right). \left( \hat{i}x + \hat{j}y +\hat{k}z \right)$

$\overrightarrow{k}.\overrightarrow{r}=x k_{x} + yk_{y} + zk_{z} $

So above equation can be written as:

$\overrightarrow{E_{x}}= E_{\circ x} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \qquad(4)$

$\overrightarrow{E_{y}}= E_{\circ y} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \qquad(5)$

$\overrightarrow{E_{z}}= E_{\circ z} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} \qquad(6)$

Now find that derivative of the equation $(4)$ along the direction of $x$ then

$\frac{\partial E_{x}}{\partial x} = i k_{x} E_{\circ x} e^{[i(x k_{x} + yk_{y} + zk_{z}) - \omega t)]} $

$\frac{\partial E_{x}}{\partial x} = i k_{x} E_{x} $

Similarly, the derivative of the equation $(5)$, and equation $(6)$ along the direction of $y$ and $z$ then

$\frac{\partial E_{y}}{\partial y} = i k_{y} E_{y} $

$\frac{\partial E_{z}}{\partial z} = i k_{z} E_{z} $

Now substitute the value of $\frac{\partial E_{x}}{\partial x}$, $\frac{\partial E_{y}}{\partial y}$, and $\frac{\partial E_{z}}{\partial z}$ in equation $(3)$

$\overrightarrow{\nabla}. \overrightarrow{E}= i k_{x} E_{x} + i k_{y} E_{y} + i k_{z} E_{z}$

$\overrightarrow{\nabla}. \overrightarrow{E}= i \left( k_{x} E_{x} + k_{y} E_{y} + k_{z} E_{z} \right)$

$\overrightarrow{\nabla}. \overrightarrow{E}= i \left( \hat{i}k_{x} + \hat{j}k_{y} + \hat{k}k_{z} \right). \left( \hat{i}E_{x} + \hat{j}E_{y} + \hat{k} E_{z} \right)$

$\overrightarrow{\nabla}. \overrightarrow{E}= i \left( \overrightarrow {k} . \overrightarrow {E} \right) \qquad(7)$

From Maxwell's first equation in free space:

$\overrightarrow{\nabla}. \overrightarrow{E}= 0 \qquad(8)$

From equation $(7)$ and equation $(8)$

$i \left( \overrightarrow {k} . \overrightarrow {E} \right)=0$

$ \overrightarrow {k} . \overrightarrow {E} = 0$

From the above equation, we can conclude that the electric field is perpendicular to the direction of propagation of the wave i.e. $\overrightarrow {E}\perp \overrightarrow {k}$

Similarly, The same result is obtained from $\overrightarrow{\nabla}. \overrightarrow {B}$ i.e. $ \overrightarrow {k} . \overrightarrow {B} = 0$, So we can conclude that the magnetic field is also perpendicular to the direction of propagation i.e. $\overrightarrow {B}\perp \overrightarrow {k}$

Thus, "The electromagnetic waves are transverse in nature"

Read More

Diamagnetic Substances and Its properties

Diamagnetic Substances :

Those substances, which are placed in the external magnetic field then they weakly magnetize in the opposite direction of the external magnetic field, are called diamagnetic substances. The susceptibility $\chi_{m} $ of diamagnetic substances is small and negative. Further, When diamagnetic substance placed in magnetic field then the flux density of the diamagnetic substance is slightly less than that in the free space. Thus, the relative permeability of diamagnetic substance $\mu_{r}$, is slightly less than 1.

Properties of Diamagnetic substances:

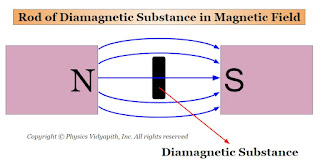
1. When a rod of a diamagnetic material is suspended freely between external magnetic poles (i.e. Between North and South Poles) then its axis becomes perpendicular to the external magnetic field $B$ (Figure). The poles produced on the two sides of the rod are similar to the poles of the external magnetic field.

2. In a non-uniform magnetic field, a diamagnetic substance tends to move from the stronger magnetic field to the weaker magnetic field. If a diamagnetic liquid is taken in a watch glass placed on two magnetic poles very near to each other, then the liquid is depressed in the middle as shown in figure below(Figure) where the field is strongest. Now, if the distance between the poles is increased, the liquid rises in the middle, because now the field is strongest near the poles.

3. If the solution of diamagnetic substance is poured into a U-tube and apply the strong magnetic field into one arm of this U-tube then the level of the solution in that arm is depressed. As shown in the figure below:

4. When diamagnetic gas molecules are passed between the poles of a magnet then diamagnetic gas molecules are spread across the field.

5. The susceptibility of a diamagnetic substance is independent of temperature.

Explanation of Diamagnetism on the Basis of Atomic Model:

The property of diamagnetism is generally found in those substances whose atoms (or ions or molecules) have an 'even' number of electrons. These even numbers of electron form pairs. In each pair of electrons, the spin of one electron is opposite to the other. So, the magnetic moment of one electron is opposite to the others because of that, the effect of magnetic dipole moments are neutralized by each other. As such, the net magnetic dipole moment of an atom (or ion or molecule) of a diamagnetic substance is zero.

When a diamagnetic substance is placed in an external magnetic field $B$ then this external magnetic field modifies the motion of the electrons in the atoms (or ions or molecules). Due to this, In each pair of electrons, the spin of one electron is become fast (Lenz's Law) and the other is slow due to that , the net magnetic dipole moment of the paired electron does not zero. Thus, a small magnetic dipole moment is induced in each atom of the substance (or ion or molecule) which is directly proportional to the magnetic field $B$ and opposite to its direction. Hence, the diamagnetic substance is magnetized opposite to the external magnetic field $B$, and the field lines become less dense inside the diamagnetic substance compared to those outside.

If the temperature of the diamagnetic substance is changed, there is no effect on its diamagnetic property. Thus, diamagnetism is temperature-independent.

Read More

Distinction between Spontaneous and Stimulated Emission of Radiation

Some of the differences between spontaneous and stimulated emission of radiation are given as follows:

1. In spontaneous emission, an atom in excited state falls to the ground state on its own without any incident photon while in stimulated emission transition takes place by stimulating photons or by an external agency.

2. In stimulated emission for each incident photon there are two outgoing photons in the same direction while in spontaneous emission the emitted photons move randomly in any direction.

3. The photons emitted in spontaneous emiss ion have a random phase and hence are incoherent while in stimulated emission the emitted photons are in phase and hence are coherent.

4. The rate of spontaneous emission is proportional to only the number of atoms in the excited state while the rate of stimulated emission is proportional to the number of atoms left in the excited state as well as on the energy density of the incident radiation.

5. In stimulated emission of radiation an amplified beam is achieved while in spontaneous emission there is no such amplification.

6. The light emitted through the spontaneous emission is not monochromatic while in stimulated transition monochromatic radiation is obtained.

7. Spontaneous emission is not controllable from outside while stimulated emission is controllable from outside.

8. In spontaneous emission, the net intensity is proportional to the number of radiating atoms while in stimulated emission it is proportional to the square of the number of radiation atoms.

Read More

Minimum Energy Or Zero Point Energy of a Particle in an one dimensional potential box or Infinite Well

Zero Point Energy of a Particle in an Infinite Well Potential Well:

The normalized wave function or eigenwave function:

$\psi_{n}(x) = \sqrt{\frac{2}{L}} sin \left( \frac{n\pi x}{L} \right)$

The probability density

$| \psi_{n}(x)|^{2} = \frac{2}{L} sin^{2} \left( \frac{n\pi x}{L} \right)$

The energy of a particle in a one-dimensional box or infinite potential well:

$E_{n}=\frac{n^{2}h^{2}}{8 mL^{2}}$

Where $n$ is called the quantum number and $n=1,2,3,4..........$ For $n=0, \psi_{n}(x)=0$ and $| \psi_{n}(x)|^{2}=0$. This shows that for $n=0$ $| \psi_{n}(x)|^{2}=0$ will be zero everywhere in the box which means that the probability of finding the particle inside the box is zero. i.e. particle is not present at all inside the box. Thus $n=0$ is not possible.

If $n\neq 0$ then $E \neq 0$. This means that the minimum energy of the particle in the box will not be zero. The minimum energy value will be obtained for the next lowest value of $n$ i.e. for $n=1$, which is

$E_{1}=\frac{h^{2}}{8 mL^{2}}$

This minimum energy of the particle is often called zero point energy which is finite inside the box. According to classical mechanics, the minimum value $E=0$ is also permissible.

Read More

Bohr's Theory of Hydrogen-Like Atoms

A hydrogen-like atom consists of a very small positively-charged nucleus and an electron revolving in a stable circular orbit around the nucleus.

The radius of electrons in stationary orbits:

Let the charge, mass, velocity of the electron and the radius of the orbit is respectively  $e$, $m$, and $v$  and $r$. The $+ze$ is the positive charge on the nucleus where $Z$ is the atomic number of the atom. As We know that when an electron revolves around the nucleus then the centripetal force on an electron is provided by the electrostatic force of attraction between the nucleus and an electron, we have

$\frac{mv^{2}}{r}=\frac{1}{4 \pi \epsilon_{\circ}} \frac{(Ze)(e)}{r^{2}}$

$mv^{2}=\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} \qquad(1)$

According to the first postulate of Bohr's model of the atom, the angular momentum of the electron is

$mvr=n \frac{h}{2 \pi} \qquad(2)$

Where $n \: (=1,2,3,.....)$ is quantum number.

Now squaring equation $(2)$ and dividing by equation $(1)$, we get

$r=n^{2} \frac{h^{2} \epsilon_{\circ}}{\pi m Z e^{2}} \qquad(3)$

The above equation is for the radii of the permitted orbits. From the above equation, this concluded that

$r \propto n^{2}$

Since, $n =1,2,3,.....$ it follows that the radii of the permitted orbits increased in the ratio $1:4:9:16:,.....$ from the first orbit.

Bohr's Radius:

For Hydrogen Atom $(z=1)$, The radius of the atom of the first orbit $(n=1)$ will be

$r_{1}= \frac{h^{2} \epsilon_{\circ}}{\pi m e^{2}}$

This is called Bohr's radius and its value is $0.53 A^{\circ}$. Since $r \propto n^{2}$, the radius of the second orbit of the hydrogen atom will be $( 4 \times 0.53 A^{\circ}) $ and that of the third orbit $9 \times 0.53 A^{\circ}$

The velocity of electrons in stationary orbits:

The velocity of the electron in permitted orbits can be obtained by the formula of equation $(2)$

$v=n\frac{h}{2 \pi m r}$

Now put the value of $r$ in above eqaution from equation $(3)$, we get

$v=\frac{Ze^{2}}{2 h \epsilon_{\circ}} \left( \frac{1}{n} \right) \quad(4)$

Thus $v \propto \frac{1}{n}$

This shows that the velocity of the electron is maximum in the lowest orbit $n=1$ and as goes on higher orbits velocity decreases.

For Hydrogen Atom $(z=1)$, The velocity of electron to move in the first orbit $(n=1)$ is

$v_{1}=\frac{e^{2}}{2h\epsilon_{\circ}}$

Its value is $2.19 \times 10^{6} m/sec$

Note:

$\frac{v_{1}}{c}= \frac{2.19 \times 10^{6}}{3 \times 10^{8}} =\frac{1}{137}$

Thus, $\frac{v_{1}}{c}$ or $\frac{e^{2}}{2h\epsilon_{\circ}}$ is a pure number. It is called the "Fine Structure Constant" and is denoted by $\alpha$

The energy of electrons in stationary orbits:

The total energy $E$ of a moving electron in an orbit is the sum of kinetic energies and potential energies. The kinetic energy of moving the electron in a stationary orbit is:

$K=\frac{1}{2} m v^{2}$

Now susbtitute the value of $v$ from equation $(1)$, we get

$K=\frac{ze^{2}}{8 \pi \epsilon_{\circ} r}$

The potential energy of a moving electron in an orbit of radius $r$ due to the electrostatic attraction between nucleus and electron is given by

$U=\frac{1}{4 \pi \epsilon_{\circ}} \frac{(Ze)(-e)}{r}$

$U=-\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} $

The total energy of the electron is

$E=K+U$

$E=\frac{ze^{2}}{8 \pi \epsilon_{\circ} r} -\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} $

$E=-\frac{ze^{2}}{8 \pi \epsilon_{\circ} r}$

Subtituting the value of $r$ in above equation from equation $(3)$, we get

$E=-\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{2}} \left( \frac{1}{n^{2}} \right) \qquad(5)$

This is the equation for the energy of the electron in the $n^{th}$ orbit.

Suppose, Excited state energy is $E_{2}$ and lower state energy is $E_{1}$. So the energy difference between these two states is:

$E_{2}- E_{1}= \frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{2}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}} \right) \qquad(6)$

According to the third postulate of Bohr's Atomic model, the frequency $\nu$ of the emitted electromagnetic wave:

$\nu=\frac{E_{2}- E_{1}}{h}$

$\nu=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right)$

The corresponding wavelength $\lambda$ of the emitted electromagnetic radiation is given by

$\frac{c}{\lambda}=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right)$

$\frac{1}{\lambda}=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(7)$

Where $\frac{1}{\lambda}$ is called "wave number" (i.e. number of waves per unit length). In the last equation$(7)$, the quantity $\frac{m e^{4}}{8 \epsilon^{2}_{\circ} c h^{3}}$ is a constant an it is known as "Rydberg Constant (R)". That is

$R = \frac{me^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} \qquad(8)$

So equation $(7)$ can be written as

$\frac{1}{\lambda}=z^{2} R \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(9)$

This is Bohr's formula for hydrogen and hydrogen-like atoms $(He^{+}, Li^{++},.......)$.

For hydrogen $Z=1$

$\frac{1}{\lambda}= R \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(10)$

The value of the Rydberg Constant is

$R = \frac{me^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} = 1.090 \times 10^{7} m^{-1}$

This value fairly agrees with empirical value $(1.097 \times 10^{7} m^{-1})$ obtained experimentally by Balmer.

The total energy in terms of Rydberg's Constant:

The $E$ expression can be written in terms of Rydberg's constant $R$ in a simplified form. So from equation $(5)$ and $(8)$ we get

$E=-Z^{2}\frac{Rhc}{n^{2}} \qquad(11)$

Putting the known values of $R$, $h$ and $c$ taking $1 eV =1.6 \times 10^{-19} \: J$ then we get

$E=-Z^{2}\frac{13.6}{n^{2}} \: eV \qquad(12)$

For a Hydrogen atom, $Z=1$

$E=-\frac{13.6}{n^{2}} \: eV \qquad(12)$

Read More

Bohr's Model of Atom

Bohr's Atomic Model Postulates:

Prof Neil in 1913 Bohr solve the difficulties of Ernest Rutherford's atomic model by applying Planck's quantum theory, For this, he proposed the following three Postulates:

1.) Electrons can revolve only in those orbits in which their angular momentum is an integral multiple of $\frac{h}{2 \pi}$. These orbits have discrete energy and definite radii. So it is called the "stable orbits". If the mass of the electron is $m$ and it is revolving with velocity $v$ in an orbit of radius $r$, then its angular momentum will be $mvr$. According to Bohr's postulate,

$mvr=\frac{nh}{2\pi}$

Where $h$ is Planck's universal constant

This Bohr's equation is called the "Bohr's quantization Condition"

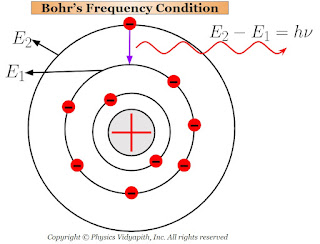
2.) When the electrons revolve in stable orbits then they do not radiate the energy in spite of their acceleration toward the center of the orbit. Hence atom remains stable and is said to exist in a stationary state.

3.) When the atoms receive energy from outside, then one (or more) of their outer electrons leaves their orbit and goes to some higher orbit. These states of the atoms are called the "excited states".

The electrons in the higher orbit stay only for $10^{-8} \: sec$ and return back to anyone lower orbit. While returning back of electrons to lower orbits, they radiate energy in the form of electromagnetic waves.

This radiated energy can be calculated by the energy difference of the electron between the two orbits (i.e. one is higher orbit and the other is lower orbit). If the energy of electron in the higher orbit is $E_{2}$ and that in the lower orbit is $E_{1}$ then net energy difference between the orbits:

$E=E_{2} - E_{1}$

$h \nu=E_{2} - E_{1} \qquad \left( \because E=h\nu \right)$

$\nu=\frac{E_{2} - E_{1}}{h}$

This Bohr's equation is called the "Bohr's frequency condition".

Read More

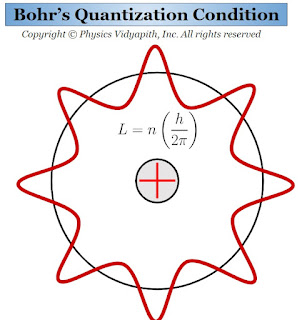
Bohr's Quantization Condition

The Quantization Condition in Bohr Theory of Hydrogen Atom:

$L=\frac{nh}{2 \pi}$

For the angular momentum L, the electron moves arbitrarily only in a stationary circular orbit. According to De Broglie's hypothesis, this condition can be easily obtained. For this purpose, there are following assumptions given below:

1.) The motion of the electron in a stationary circular orbit is represented by a standing matter-wave. If the wavelength of the wave is $\lambda$ then the De Broglie relation

$\lambda=\frac{h}{mv} \qquad(1)$

Where
$m \rightarrow$ The mass of the electron and
$v \rightarrow$ The Velocity in the orbit.

2.) The circular orbit contains an integral number of wavelengths, i.e.

$2 \pi r_{n}= n \lambda $

$\frac{2 \pi r_{n}}{\lambda}= n \qquad(2)$

Where $n=1,2,3............$ and $r_{n}$ is the radius of the orbit.

Substituting the value of $\lambda$ in equation$(2)$

$\frac{2 \pi r_{n} m v}{h} =n$

$mvr_{n} =\frac{nh}{2\pi}$

$L=\frac{nh}{2\pi}$

Which is Bohr's quantization condition.

Read More

Drawbacks of Old Quantum Theory

Planck's quantum hypothesis with its application and extension to explain the black body radiation like the photo-electric effect, the Compton effect, the variation of specific heat of solid with temperature and the spectrum of hydrogen is now called the Old quantum theory. Through these phenomena are successfully explained by the theory, there are numerous drawbacks of the theory. A few of them are as follows.

1.) Bohr's quantization rules are arbitrary. The theory does not provide a physical explanation for the assumptions.

2.) The old quantum theory cannot be applied to explain the spectra of helium and of more complex atoms.

3.) It can provide only a qualitative and incomplete explanation of the intensities of the spectral lines.

4.) It can not explain the dispersion of light.

5.) The theory of non-harmonic vibrations of systems cannot be applied to explain the vibrations of systems.

Read More

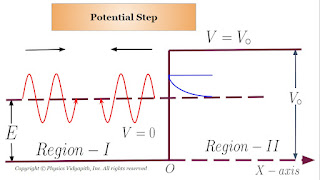
One dimensional Step Potential Barrier for a Particle

Potential Step:

1.) In region $(I)$  i.e.$(-\infty \leq \: x \lt \: 0)$
2.) In region $(II)$ i.e. $(0 \leq \:x \: \leq +\infty)$
Case $(1)$	When $E \lt V_{\circ}$
A.) Expression for the Amplitudes $B$ and $C$ in terms of the Amplitude $A$ B.) Expression for the wave function in the region $(I)$ and $(II)$ C.) Expression for the Probability Current Densities D.) Reflection and Transmission Coefficients
Case $(2)$ :	When $E \gt V_{\circ}$
A.) Expression for the Amplitudes $B$ and $C$ in terms of the Amplitude $A$ B.) Expression for the wave function in the region $(I)$ and $(II)$ C.) Expression for the Probability Current Densities D.) Reflection and Transmission Coefficients

One dimensional step potential barrier for a particle is shown in the figure below.

The meaning of the figure is that the region $(I)$ is at left hand side of the origin $O$ and the potential energy of a particle is zero in this region $(I)$. The region $(II)$ is at the right hand side of $O$ and this region $II$ has constant potential equal to $V_{\circ}$. Such a potential barrier does not exist in nature, but it is approximately similar to the instantaneous potential difference between the dees of a cyclotron or the surface potential barrier of a metal.

Suppose a uniform beam of particles each of mass $m$ and having kinetic energy $E$ is traveling parallel to the x-axis from left to right in the region $(I)$, and is incident on the potential step. In region $(I)$ the energy $E$ of a particle is whole kinetic energy, and in region $(II)$ it is partly kinetic and partly potential energy.

If $E \lt V_{\circ}$, then according to classical mechanics, a particle can enter in the region $(II)$. However according to quantum mechanics although the wave function for an incident particle has a finite value in the region $(II)$ there is no steady transmission of the particle has finite value in this region $(II)$, all the particles are reflected back from the potential step $V_{\circ} \gt E$. In the following discussion, we investigate this behavior of the particles.

Let $\psi_{1}(x)$ and $\psi_{2}(x)$ be the wave function for the motion of a particle in the beam in the region $(I)$ and $(II)$ respectively.

1.) In region $(I)$ i.e. $(-\infty \leq \: x \lt \: 0)$:

According to the time-independent Schrodinger wave equation is:

$-\frac{\hbar^{2}}{2m} \frac{d^{2} \psi_{1}}{dx^{2}}=E \psi_{1}$

$\frac{d^{2} \psi_{1}}{dx^{2}} + \frac{2mE}{\hbar^{2}} \psi_{1} =0$

Let $k_{1}^{2}=\frac{2mE}{\hbar^{2}} $, Now substitute this value in the above equation that can be written as

$\frac{d^{2} \psi_{1}}{dx^{2}} + k_{1}^{2} \psi_{1} =0 \qquad(1)$

2.) In region $(II)$ i.e. $(0 \leq \:x \: \leq +\infty)$:

Case $(1)$ : When $E \lt V_{\circ}$

Then according to the time-independent Schrodinger wave equation for the above case is:

$\frac{d^{2} \psi_{2}}{dx^{2}} + \frac{2m \left(E-V_{\circ} \right)}{\hbar^{2}} \psi_{2} =0$

$\frac{d^{2} \psi_{2}}{dx^{2}} - \frac{2m \left(V_{\circ} -E \right)}{\hbar^{2}} \psi_{2} =0$

Let $\beta^{2}=\frac{2m\left(V_{\circ} -E \right)}{\hbar^{2}} $, Now substitute this value in the above equation that can be written as

$\frac{d^{2} \psi_{2}}{dx^{2}} - \beta^{2} \psi_{2} =0 \qquad(2)$

The general solution of the equation $(1)$ and equation $(2)$ is

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad(3)$

$\psi_{2} (x) = C e^{- \beta \: x} + D e^{\beta \: x} \qquad(4)$

In equation $(3)$ the term $A e^{ik_{1}x}$ represents a wave of amplitude $A$ traveling in the positive x-axis direction and term $B e^{-ik_{1}x} $ is the wave of amplitude $B$ reflected from potential step in the negative x-axis direction. In equation $(4)$ the term $C e^{- \beta \: x}$ is an exponentially decreasing wave function representing a non-oscillatory disturbance that penetrates the potential barrier for some finite distance in the positive x-axis direction and the term $D e^{\beta \: x}$ is an exponentially increasing wave function in the positive x-axis direction. According to the physical interpretation, wave function $\psi$ must remain finite when $x$ approaches $\infty$. From this condition, it follows that $D=0$. Hence in the region $(II)$, the valid solution of the wave equation is:

$\psi_{2} (x) = C e^{- \beta \: x} \qquad(5)$

A.) Expression for the Amplitudes $B$ and $C$ in terms of the Amplitude $A$:

i) At $x=0$, we have

$\psi_{1}(0) = \psi_{2}(0)$

So from equation $(3)$ and equation $(5)$, we have

$A+B=C \qquad(6)$

ii) We also have

$\left( \frac{d\psi_{1}}{dx} \right)_{x=0} = \left( \frac{d\psi_{2}}{dx} \right)_{x=0}$

So again from equation $(3)$ and equation $(5)$, we have

$A\:i\:k_{1} - B\:i\:k_{1} = - C \: \beta$

$A - B = - \frac{C \: \beta}{i\:k_{1} }$

$A - B = \frac{iC \: \beta}{k_{1} } \qquad(7)$

Adding equation $(6)$ and equation $(7)$

$2A = \left( 1 + \frac{ i \beta}{k_{1}} \right)C$

$2A = \left(\frac{k_{1} + i \beta}{k_{1}} \right)C$

$C = \left(\frac{2k_{1} }{k_{1} + i \beta} \right)A \qquad(8)$

Now subtracting the equation $(7)$ from equation $(6)$

$2B = \left( 1 - \frac{ i \beta}{k_{1}} \right)C$

$2B = \left(\frac{k_{1} - i \beta}{k_{1}} \right)C$

Now substitute the value of $C$ from equation $(8)$ in the above equation then we get

$2B = \left(\frac{k_{1} - i \beta}{k_{1}} \right) \left(\frac{2k_{1} }{k_{1} + i \beta} \right)A$

$B = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} \right)A \qquad(9)$

The equation $(8)$ and equation $(9)$ can be expressed in polar form.

Let $k_{1}= r \: cos\delta$ and $\beta=r\: sin \delta$

Then $r=\sqrt {k_{1}^{2} + \beta^{2}}$ and $tan \delta =\frac{\beta}{k_{1}}$

Now subtitute the value of $k_{1}$ and $\beta$ in equation $(9)$

Now substitute the value of $k_{1}$ and $\beta$ in equation $(9)$

$B = \left(\frac{r \: cos\delta - i r\: sin \delta}{r \: cos\delta + i r\: sin \delta} \right)A $

$B = \left(\frac{ \: cos\delta - i \: sin \delta}{ \: cos\delta + i \: sin \delta} \right)A $

$B = \left(\frac{ e^{-i\delta}}{ e^{i\delta}} \right)A $

$B = e^{-2i \delta} A \qquad(10) $

Now from eqaution $(8)$

$C = \left(\frac{2k_{1} }{k_{1} + i \beta} - 1 + 1 \right)A $

$C = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} +1 \right)A $

Now substitute the value of $k_{1}$ and $\beta$ in equation $(8)$

$C = \left(\frac{r \: cos\delta - i r\: sin \delta}{r \: cos\delta + i r\: sin \delta} +1 \right)A $

$C = \left(\frac{ \: cos\delta - i \: sin \delta}{ \: cos\delta + i \: sin \delta} +1 \right)A $

$C = \left(e^{-2i \delta} +1 \right)A \qquad(11)$

B.) Expression for the wave function in the region $(I)$ and $(II)$:

(i.) In region $(I)$: $x \lt 0$:

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ from \: eqaution \: (3) \right\}$

Now substitute the value of $B$ in the above equation:

$\psi_{1} (x) = A e^{ik_{1}x} + e^{-2i \delta} A e^{-ik_{1}x} $

$\psi_{1} (x) = A e^{-i \delta} \left( e^{ik_{1}x} e^{i \delta} + e^{-i \delta} A e^{-ik_{1}x} \right) $

$\psi_{1} (x) = 2A e^{-i \delta} \left[ \frac{e^{ik_{1}x} e^{i \delta} + e^{-i \delta} A e^{-ik_{1}x}}{2} \right] $

$\psi_{1} (x) = 2A e^{-i \delta} cos \left(k_{1}x + \delta \right) \qquad(12) $

(ii.) In region $(II)$: $x \gt 0$:

$\psi_{2} (x) = C e^{- \beta \: x} \qquad \left\{ from \: eqaution \: (5) \right\}$

Now substitute the value of $C$ in the above equation:

$\psi_{2} (x) = \left(e^{-2i \delta} +1 \right)A e^{- \beta \: x} $

$\psi_{2} (x) = A e^{-i \delta} \left(e^{-i \delta} +e^{i \delta} \right) e^{- \beta \: x} $

$\psi_{2} (x) = 2A e^{-i \delta} \left( \frac{e^{-i \delta} +e^{i \delta}}{2} \right) e^{- \beta \: x} $

$\psi_{2} (x) = 2A e^{-i \delta} \left( \frac{e^{-i \delta} +e^{i \delta}}{2} \right) e^{- \beta \: x} $

$\psi_{2} (x) = \left( 2A e^{-i \delta} cos \delta \right) e^{- \beta \: x} \qquad(13)$

This shows that the wave function in the region $(II)$ is exponentially damped.

C.) Expression for the Probability Current Densities:

(i.) In region $(I)$:

a.) The probabilty current density $S_{1}$ for the incident beam of particle is given by

$S_{i} =(Incident \: wave \: function)(Complex \: conjugate \: of \: incident \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{i} =(A e^{ik_{1}x})(A e^{ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} e^{ik_{1}x} e^{-ik_{1}x} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} \frac{\hbar k_{1}}{m}$

$S_{i} = | A|^{2} \frac{\hbar k_{1}}{m} \qquad(14)$

b.) The probability current density $S_{r}$ for the reflected beam of particles is given by:

$S_{r} =(Reflected \: wave \: function)(Complex \: conjugate \: of \: reflected \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{r} =(B e^{-ik_{1}x})(B e^{-ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{r} = | B |^{2} \frac{\hbar k_{1}}{m} \qquad(15)$

Hence the net probability current density in the region $(I)$ is given by

$S=S_{i} - S_{r}$

$S=\frac{\hbar k_{1}}{m} \left(| A |^{2} - | B |^{2} \right) \qquad(16)$

The intensity of waves:

We know that

$B = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} \right)A \qquad \left\{ From \: equation \: (9) \right\}$

The complex conjugate of this equation is:

$B^{*} = \left(\frac{k_{1} + i \beta}{k_{1} - i \beta} \right)A^{*} $

$BB^{*}=AA^{*}$

$ | B^{2} | = | A^{2}| \qquad(17)$

Hence the net probability current in the region $(I)$ to the left of the region $O$ is zero.

The equation $ | B^{2} | = | A^{2}|$ shows that the intensity of the reflected wave is equal to that of the incident wave, or the number of particles per second passing normally through the unit area of the incident beam is equal to the number of particles per second passing normally through unit area of the reflected beam. Consequently, the incident and reflected probability currents cancel one another.

(ii.) In region $(II)$:

From the relation $ | B^{2} | = | A^{2}|$ we infer that the probability current density in the region $(II)$ to the right of the origin should be zero. However, we can prove this conclusion using the wave function

$\psi_{2}= C e^{-\beta x}$

and its complex conjugate

$\psi^{*}_{2}= C^{*} e^{-\beta x}$

The proof is as follows:

The probability current density in the region $(II)$ for the transmitted beam of the particles is given by

$S_{t}= -\frac{i \hbar}{2m} \left[ \psi^{*}_{2} \frac{\partial \psi_{2}}{\partial x} - \psi_{2} \frac{\partial \psi^{*}_{2}}{\partial x} \right]$

Now Substitute the value of $\psi$ and $\psi^{*}$ in this above equation:

$S_{t}= -\frac{i \hbar}{2m} \left[C^{*} e^{-\beta x} \frac{\partial C e^{-\beta x}}{\partial x} - C e^{-\beta x} \frac{\partial C^{*} e^{-\beta x}}{\partial x} \right]$

$S_{t}= -\frac{i \hbar}{2m} \left[CC^{*} e^{-\beta x} \frac{\partial e^{-\beta x}}{\partial x} - CC^{*} e^{-\beta x} \frac{\partial e^{-\beta x}}{\partial x} \right]$

$S_{t}= -\frac{i \hbar}{2m} \left[CC^{*} e^{-\beta x} (-\beta) e^{-\beta x} - CC^{*} e^{-\beta x} (-\beta) e^{-\beta x} \right]$

$S_{t}= -\frac{i \hbar}{2m} \left[-CC^{*} e^{-2\beta x} (\beta) + CC^{*} e^{-2\beta x} (\beta) \right]$

$S_{t}=0 \qquad(18)$

The probability current density $S_{t}$ for a transmitted beam of particles is zero

D.) Reflection and Transmission Coefficients:

(i.)Reflection Coefficients:

The reflection coefficient $R$ is defined as the ratio of the probability current density $S_{r}$ for the reflected beam of particles to the probability current density $S_{i}$ for the incident beam of particles. Thus it is given by

$R=\frac{S_{r}}{S_{i}}$

$R=\frac{| B |^{2} \frac{\hbar k_{1}}{m}}{ | A |^{2} \frac{\hbar k_{1}}{m} }$

$R=\frac{| B |^{2} }{| A |^{2}} \qquad(19)$

In this case $(V_{\circ} \gt E)$, $ | B^{2} | = | A^{2}|$ Now the above equation $(19)$ can be written as

$R=1 \qquad(20)$

This shows that the reflection of the incident beam, at the potential step is total.

(ii) Transmission Coefficients:

The transmission coefficient $T$ is defined as the ratio of the probability current density $S_{t}$ for the transmitted beam of the particle to the probability current density $S_{i}$ for the incident beam. Thus it is given by

$T=\frac{S_{t}}{S_{i}} \qquad(21)$

In this case: The probability of current densityin region $(II)$ is zero i.e. $S_{t}=0$ then transmission coefficient

$T=0$

So from above equation, we can conclude that the transmission coefficient of the beam of particles is zero.

Conclusions:

From the foregoing discussion, we draw the following inference:

i.) The reflection of the incident beam of particles, at the potential step is total.

ii.) There is no probability of current density anywhere. To the left hand side of the potential step, the incident and the reflected probability of currents density cancel to each other, and to the right ahnd side of the step, probability of currents density is zero.

iii.) To the right of the step the wave function is not zero, but it is exponentially damped. Therefore there is a finite or definite probability of finding the particle in the region $(II)$

If $V_{\circ} \rightarrow \infty$ and $E$ is finite, then

$\beta=\sqrt {\frac{2m \left( V_{\circ} -E \right)}{\hbar^{2}}} \rightarrow \infty $

In this case the wave function in region $(II)$ is $\psi_{2}= C \: e^{-\beta x} \rightarrow 0 $

$B = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} \right)A $, and $C = \left(\frac{2k_{1} }{k_{1} + i \beta} \right)A$

$\underset{\beta \rightarrow \infty}{Lim} \:\: \frac{B}{A}=\frac{\frac{k_{1}}{\beta} - i}{\frac{k_{1}}{\beta}+i} = -1$

$\frac{B}{A} =-1$ Or $A+B=0$ $\qquad(22)$

And, $\underset{\beta \rightarrow \infty}{Lim} \:\: \frac{C}{A}=\frac{2k_{1}} {k_{1}+i \beta} = 0$

$C=0 \qquad(23)$

Or

Hence the wave function

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ From \: equation (3) \right\}$

At $x=0$ is

$\psi_{1} (0) = A + B=0 \qquad(24)$

And the wave function $\psi_{2}= C \: e^{-\beta x}$

At $x=0$ is $\psi_{2}=C=0$

The slope of $\psi_{1}$ at $x=0$ is

$\left( \frac{d\psi_{1}}{dx} \right)_{x=0}= ik_{1} \left( A-B \right) = 2 i k_{1} A \qquad(25)$

Thus at a point where the potential suddenly increases from zero to an infinite value the wave function $\psi_{1}$ becomes zero and ts slope suddenly falls from a finite value $2ik_{1}A$ to zero.

In region $(II)$ : $(0 \leq \:x \: \leq +\infty)$:

Case $(2)$ : When $E \gt V_{\circ}$

If $E \gt V_{\circ}$, then the time-independent Schrodinger wave equation is

$\frac{d^{2} \psi_{2}}{dx^{2}} + \frac{2m \left(E-V_{\circ} \right)}{\hbar^{2}} \psi_{2} =0$

Let $k_{2}^{2}=\frac{2m \left(E-V_{\circ} \right)}{\hbar^{2}}$, Now put this value in the above equation which can be written as

$\frac{d^{2} \psi_{2}}{dx^{2}} - k_{2}^{2} \psi_{2} =0 \qquad(26)$

The general solution of the equation $(26)$ is

$\psi_{2} (x) = G e^{ik_{2}x} + H e^{-ik_{1}x} \qquad(27)$

In this equation the term $G e^{ik_{2}x}$ represents a wave traveling from the potential step in the positive x-direction, and the term $H e^{-ik_{1}x}$ a wave traveling in the negative x-direction towards the potential step. Since the particles are incident only from the left of the potential step $H$ must be zero. Hence in the region, $(II)$ the valid solution of the wave equation is

$\psi_{2} (x) = G e^{ik_{2}x} \qquad(28)$

A.) Expression for the Amplitudes $B$ and $G$ in terms of the Amplitude $A$:

i) At $x=0$, we have

$\psi_{1}(0) = \psi_{2}(0)$

So from equation $(3)$ and equation $(28)$, we have

$A+B=G \qquad(29)$

ii) At this condition that the derivative of the wave function is continuous at $x=0$

$\left( \frac{d\psi_{1}}{dx} \right)_{x=0} = \left( \frac{d\psi_{2}}{dx} \right)_{x=0}$

$A \: ik_{1} - B \: ik_{1} =G \: ik_{2} $

$A-B =\frac{k_{2}}{k_{1}}G \qquad(30)$

Adding equation $(29)$ and equation $(30)$, we get

$2A=\left(\frac{k_{1}+k_{2}}{k_{1}}\right) G$

$G=\left(\frac{2k_{1}}{k_{1} +k_{2}}\right) A \qquad(31)$

Subtracting equation $(30)$ and equation $(29)$, we get

$2B=\left(\frac{k_{1} - k_{2}}{k_{1}}\right) G$

Now subtitute the vaue of $G$ from equation $(31)$ to the above equation

$2B=\left(\frac{k_{1} - k_{2}}{k_{1}}\right) \left(\frac{2k_{1}}{k_{1} +k_{2}}\right) A$

$B=\left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right) A \qquad(32)$

B.) Expression for the wave function in region $(I)$ and $(II)$

(i.) In region $(I)$: $x \lt 0$:

$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ from \: eqaution \: (3) \right\}$

$\psi_{1} = A \left[ e^{ik_{1}x} + \left( \frac{k_{1} - k_{2}}{k_{1} +k_{2}} \right) e^{-ik_{1}x} \right] \qquad(33)$

ii.) In region $(II)$: $x \gt 0$:

$\psi_{2} (x) = G e^{ i k_{2} \: x} \qquad \left\{ from \: eqaution \: (28) \right\}$

$\psi_{2} (x) = \left(\frac{2k_{1}}{k_{1} +k_{2}}\right) A e^{ i k_{2} \: x} \qquad (34)$

C.) Expression for the Probability Current Densities:

(i.) In region $(I)$:

a.) The probabilty current density $S_{1}$ for the incident beam of particle is given by

$S_{i} =(Incident \: wave \: function)(Complex \: conjugate \: of \: incident \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{i} =(A e^{ik_{1}x})(A e^{ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} e^{ik_{1}x} e^{-ik_{1}x} \frac{\hbar k_{1}}{m}$

$S_{i} =A A^{*} \frac{\hbar k_{1}}{m}$

$S_{i} = | A |^{2} \frac{\hbar k_{1}}{m} \qquad(35)$

b.) The probability current density $S_{r}$ for the reflected beam of particles is given by:

$S_{r} =(Reflected \: wave \: function)(Complex \: conjugate \: of \: reflected \: wave \: function) \frac{\hbar k_{1}}{m}$

$S_{r} =(B e^{-ik_{1}x})(B e^{-ik_{1}x})^{*} \frac{\hbar k_{1}}{m}$

$S_{r} = | B |^{2} \frac{\hbar k_{1}}{m} \qquad(36)$

Hence the net probability current density in the region $(I)$ is given by

$S=S_{i} - S_{r}$

$S=\frac{\hbar k_{1}}{m} \left(| A |^{2} - | B |^{2} \right) \qquad(37)$

From equation $(32)$

$|B|^{2}=\left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right)^{2} |A|^{2}$

Substitute the above equation value in equation $(37)$

$S=\frac{\hbar k_{1}}{m} \left(| A |^{2} - \left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right)^{2} |A|^{2} \right)$

$S=\frac{\hbar k_{1}}{m} | A |^{2} \left[ 1 - \left(\frac{k_{1} - k_{2}}{k_{1} +k_{2}}\right)^{2} \right]$

$S=\frac{\hbar k_{1}}{m} |A|^{2} \left[ \frac{4 k_{1} k_{2}}{\left(k_{1} +k_{2} \right)^{2}} \right]$

$S=\frac{4 k_{1} k_{2}}{\left(k_{1} +k_{2}\right)^{2}} \left( \frac{\hbar k_{1}}{m} \right) | A |^{2} \qquad(38)$

(ii.) In region $(II)$:

The probability current density $S_{t}$ for the transmitted beam of particles in region $(II)$ is given by

$S_{t}= \left( G e^{ i k_{2} \: x} \right) \left( G e^{ i k_{2} \: x} \right)^{*} \frac{\hbar k_{2}}{m} $

$S_{t}= \frac{\hbar k_{2}}{m} |G|^{2} \qquad(39)$

From equation $(31)$, we have

$|G|^{2}=\left(\frac{2k_{1}}{k_{1} +k_{2}}\right)^{2} |A|^{2}$

So substitute the value of the above equation in equation $(39)$, then we get

$S_{t}= \frac{\hbar k_{2}}{m} \left(\frac{2k_{1}}{k_{1} +k_{2}}\right)^{2} |A|^{2}$

$S_{t}= \frac{4k^{2}_{1}}{\left(k_{1} +k_{2}\right)^{2}} \left( \frac{\hbar k_{2}}{m} \right) |A|^{2} \qquad(40)$

The equation $(38)$ and equation $(40)$ shows that $S=S_{t}$. i.e. The net probability density in the direction from left to right in the region $(I)$ is equal to the probability current density in the region $(II)$.

D.) Reflection and Transmission Coefficients:

(i.)Reflection Coefficients:

The reflection coefficient $R$ is defined as the ratio of the probability current density $S_{r}$ for the reflected beam of particles to the probability current density $S_{i}$ for the incident beam of particles. Thus it is given by

$R=\frac{S_{r}}{S_{i}}$

$R=\frac{| B |^{2} \frac{\hbar k_{1}}{m}}{ | A |^{2} \frac{\hbar k_{1}}{m} }$

$R=\frac{| B |^{2} }{| A |^{2}}$

Now using the equation $(32)$ we get

$R=\frac{\left( k_{1} -k_{2} \right)}{\left( k_{1} + k_{2} \right)} \qquad(41)$

(ii) Transmission Coefficients:

The transmission coefficient $T$ is defined as the ratio of the probability current density $S_{t}$ for the transmitted beam of the particle to the probability current density $S_{i}$ for the incident beam. Thus it is given by

$T=\frac{S_{t}}{S_{i}} $

$T=\frac{| G |^{2} \frac{\hbar k_{2}}{m}}{ | A |^{2} \frac{\hbar k_{1}}{m} }$

$T=\frac{| G |^{2} k_{2}}{ | A |^{2} k_{1} }$

Now using equation $(31)$, we get

$T= \frac{k_{2}}{k_{1}} \left( \frac{2 k_{1}}{k_{1} + k_{2}} \right)^{2}$

$T= \frac{k_{2}}{k_{1}} \frac{4 k^{2}_{1}}{\left( k_{1} + k_{2} \right)^{2}} \qquad(42)$

Adding the equation $(41)$ and equation $(42)$ it is easily verified that

$R+T=1 \qquad(43)$

Read More