A hydrogen-like atom consists of a very small positively-charged nucleus and an electron revolving in a stable circular orbit around the nucleus.
The radius of electrons in stationary orbits:
Let the charge, mass, velocity of the electron and the radius of the orbit is respectively $e$, $m$, and $v$ and $r$. The $+ze$ is the positive charge on the nucleus where $Z$ is the atomic number of the atom. As We know that when an electron revolves around the nucleus then the centripetal force on an electron is provided by the electrostatic force of attraction between the nucleus and an electron, we have
$\frac{mv^{2}}{r}=\frac{1}{4 \pi \epsilon_{\circ}} \frac{(Ze)(e)}{r^{2}}$
$mv^{2}=\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} \qquad(1)$
According to the first postulate of Bohr's model of the atom, the angular momentum of the electron is
$mvr=n \frac{h}{2 \pi} \qquad(2)$
Where $n \: (=1,2,3,.....)$ is quantum number.
Now squaring equation $(2)$ and dividing by equation $(1)$, we get
$r=n^{2} \frac{h^{2} \epsilon_{\circ}}{\pi m Z e^{2}} \qquad(3)$
The above equation is for the radii of the permitted orbits. From the above equation, this concluded that
$r \propto n^{2}$
Since, $n =1,2,3,.....$ it follows that the radii of the permitted orbits increased in the ratio $1:4:9:16:,.....$ from the first orbit.
Bohr's Radius:
For Hydrogen Atom $(z=1)$, The radius of the atom of the first orbit $(n=1)$ will be
$r_{1}= \frac{h^{2} \epsilon_{\circ}}{\pi m e^{2}}$
This is called Bohr's radius and its value is $0.53 A^{\circ}$. Since $r \propto n^{2}$, the radius of the second orbit of the hydrogen atom will be $( 4 \times 0.53 A^{\circ}) $ and that of the third orbit $9 \times 0.53 A^{\circ}$
The velocity of electrons in stationary orbits:
The velocity of the electron in permitted orbits can be obtained by the formula of equation $(2)$
$v=n\frac{h}{2 \pi m r}$
Now put the value of $r$ in above eqaution from equation $(3)$, we get
$v=\frac{Ze^{2}}{2 h \epsilon_{\circ}} \left( \frac{1}{n} \right) \quad(4)$
Thus $v \propto \frac{1}{n}$
This shows that the velocity of the electron is maximum in the lowest orbit $n=1$ and as goes on higher orbits velocity decreases.
For Hydrogen Atom $(z=1)$, The velocity of electron to move in the first orbit $(n=1)$ is
$v_{1}=\frac{e^{2}}{2h\epsilon_{\circ}}$
Its value is $2.19 \times 10^{6} m/sec$
Note:
$\frac{v_{1}}{c}= \frac{2.19 \times 10^{6}}{3 \times 10^{8}} =\frac{1}{137}$
Thus, $\frac{v_{1}}{c}$ or $\frac{e^{2}}{2h\epsilon_{\circ}}$ is a pure number. It is called the "Fine Structure Constant" and is denoted by $\alpha$
The energy of electrons in stationary orbits:
The total energy $E$ of a moving electron in an orbit is the sum of kinetic energies and potential energies. The kinetic energy of moving the electron in a stationary orbit is:
$K=\frac{1}{2} m v^{2}$
Now susbtitute the value of $v$ from equation $(1)$, we get
$K=\frac{ze^{2}}{8 \pi \epsilon_{\circ} r}$
The potential energy of a moving electron in an orbit of radius $r$ due to the electrostatic attraction between nucleus and electron is given by
$U=\frac{1}{4 \pi \epsilon_{\circ}} \frac{(Ze)(-e)}{r}$
$U=-\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} $
The total energy of the electron is
$E=K+U$
$E=\frac{ze^{2}}{8 \pi \epsilon_{\circ} r} -\frac{Ze^{2}}{4 \pi \epsilon_{\circ} r} $
$E=-\frac{ze^{2}}{8 \pi \epsilon_{\circ} r}$
Subtituting the value of $r$ in above equation from equation $(3)$, we get
$E=-\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{2}} \left( \frac{1}{n^{2}} \right) \qquad(5)$
This is the equation for the energy of the electron in the $n^{th}$ orbit.
Suppose, Excited state energy is $E_{2}$ and lower state energy is $E_{1}$. So the energy difference between these two states is:
$E_{2}- E_{1}= \frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{2}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}} \right) \qquad(6)$
According to the third postulate of Bohr's Atomic model, the frequency $\nu$ of the emitted electromagnetic wave:
$\nu=\frac{E_{2}- E_{1}}{h}$
$\nu=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right)$
The corresponding wavelength $\lambda$ of the emitted electromagnetic radiation is given by
$\frac{c}{\lambda}=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right)$
$\frac{1}{\lambda}=\frac{mz^{2}e^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(7)$
Where $\frac{1}{\lambda}$ is called "wave number" (i.e. number of waves per unit length). In the last equation$(7)$, the quantity $\frac{m e^{4}}{8 \epsilon^{2}_{\circ} c h^{3}}$ is a constant an it is known as "Rydberg Constant (R)". That is
$R = \frac{me^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} \qquad(8)$
So equation $(7)$ can be written as
$\frac{1}{\lambda}=z^{2} R \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(9)$
This is Bohr's formula for hydrogen and hydrogen-like atoms $(He^{+}, Li^{++},.......)$.
For hydrogen $Z=1$
$\frac{1}{\lambda}= R \left( \frac{1}{n_{1}^{2}} -\frac{1}{n_{2}^{2}}\right) \qquad(10)$
The value of the Rydberg Constant is
$R = \frac{me^{4}}{8 \epsilon^{2}_{\circ} c h^{3}} = 1.090 \times 10^{7} m^{-1}$
This value fairly agrees with empirical value $(1.097 \times 10^{7} m^{-1})$ obtained experimentally by Balmer.
The total energy in terms of Rydberg's Constant:
The $E$ expression can be written in terms of Rydberg's constant $R$ in a simplified form. So from equation $(5)$ and $(8)$ we get
$E=-Z^{2}\frac{Rhc}{n^{2}} \qquad(11)$
Putting the known values of $R$, $h$ and $c$ taking $1 eV =1.6 \times 10^{-19} \: J$ then we get
$E=-Z^{2}\frac{13.6}{n^{2}} \: eV \qquad(12)$
For a Hydrogen atom, $Z=1$
$E=-\frac{13.6}{n^{2}} \: eV \qquad(12)$
Bohr's Model of Atom
Bohr's Atomic Model Postulates:
Prof Neil in 1913 Bohr solve the difficulties of Ernest Rutherford's atomic model by applying Planck's quantum theory, For this, he proposed the following three Postulates:
1.) Electrons can revolve only in those orbits in which their angular momentum is an integral multiple of $\frac{h}{2 \pi}$. These orbits have discrete energy and definite radii. So it is called the "stable orbits". If the mass of the electron is $m$ and it is revolving with velocity $v$ in an orbit of radius $r$, then its angular momentum will be $mvr$. According to Bohr's postulate,
$mvr=\frac{nh}{2\pi}$
Where $h$ is Planck's universal constant
This Bohr's equation is called the "Bohr's quantization Condition"
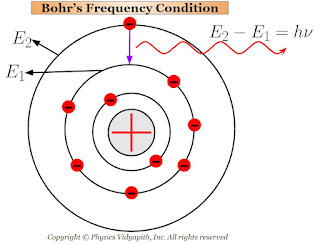
2.) When the electrons revolve in stable orbits then they do not radiate the energy in spite of their acceleration toward the center of the orbit. Hence atom remains stable and is said to exist in a stationary state.
3.) When the atoms receive energy from outside, then one (or more) of their outer electrons leaves their orbit and goes to some higher orbit. These states of the atoms are called the "excited states".
The electrons in the higher orbit stay only for $10^{-8} \: sec$ and return back to anyone lower orbit. While returning back of electrons to lower orbits, they radiate energy in the form of electromagnetic waves.
This radiated energy can be calculated by the energy difference of the electron between the two orbits (i.e. one is higher orbit and the other is lower orbit). If the energy of electron in the higher orbit is $E_{2}$ and that in the lower orbit is $E_{1}$ then net energy difference between the orbits:
$E=E_{2} - E_{1}$
$h \nu=E_{2} - E_{1} \qquad \left( \because E=h\nu \right)$
$\nu=\frac{E_{2} - E_{1}}{h}$
This Bohr's equation is called the "Bohr's frequency condition".
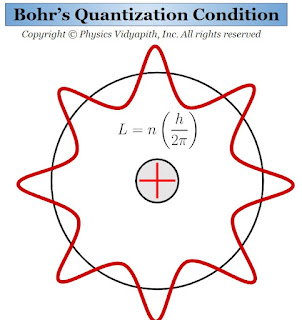
Bohr's Quantization Condition
The Quantization Condition in Bohr Theory of Hydrogen Atom:
$L=\frac{nh}{2 \pi}$
For the angular momentum L, the electron moves arbitrarily only in a stationary circular orbit. According to De Broglie's hypothesis, this condition can be easily obtained. For this purpose, there are following assumptions given below:
1.) The motion of the electron in a stationary circular orbit is represented by a standing matter-wave. If the wavelength of the wave is $\lambda$ then the De Broglie relation
$\lambda=\frac{h}{mv} \qquad(1)$
Where
$m \rightarrow$ The mass of the electron and
$v \rightarrow$ The Velocity in the orbit.
2.) The circular orbit contains an integral number of wavelengths, i.e.
$2 \pi r_{n}= n \lambda $
$\frac{2 \pi r_{n}}{\lambda}= n \qquad(2)$
Where $n=1,2,3............$ and $r_{n}$ is the radius of the orbit.
Substituting the value of $\lambda$ in equation$(2)$
$\frac{2 \pi r_{n} m v}{h} =n$
$mvr_{n} =\frac{nh}{2\pi}$
$L=\frac{nh}{2\pi}$
Which is Bohr's quantization condition.
$m \rightarrow$ The mass of the electron and
$v \rightarrow$ The Velocity in the orbit.
Drawbacks of Old Quantum Theory
Planck's quantum hypothesis with its application and extension to explain the black body radiation like the photo-electric effect, the Compton effect, the variation of specific heat of solid with temperature and the spectrum of hydrogen is now called the Old quantum theory. Through these phenomena are successfully explained by the theory, there are numerous drawbacks of the theory. A few of them are as follows.
1.) Bohr's quantization rules are arbitrary. The theory does not provide a physical explanation for the assumptions.
2.) The old quantum theory cannot be applied to explain the spectra of helium and of more complex atoms.
3.) It can provide only a qualitative and incomplete explanation of the intensities of the spectral lines.
4.) It can not explain the dispersion of light.
5.) The theory of non-harmonic vibrations of systems cannot be applied to explain the vibrations of systems.
One dimensional Step Potential Barrier for a Particle
$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ from \: eqaution \: (3) \right\}$
$\psi_{2} (x) = C e^{- \beta \: x} \qquad \left\{ from \: eqaution \: (5) \right\}$
$S_{i} =(Incident \: wave \: function)(Complex \: conjugate \: of \: incident \: wave \: function) \frac{\hbar k_{1}}{m}$
$S_{r} =(Reflected \: wave \: function)(Complex \: conjugate \: of \: reflected \: wave \: function) \frac{\hbar k_{1}}{m}$
$B = \left(\frac{k_{1} - i \beta}{k_{1} + i \beta} \right)A \qquad \left\{ From \: equation \: (9) \right\}$
$S_{t}= -\frac{i \hbar}{2m} \left[C^{*} e^{-\beta x} \frac{\partial C e^{-\beta x}}{\partial x} - C e^{-\beta x} \frac{\partial C^{*} e^{-\beta x}}{\partial x} \right]$
$S_{t}= -\frac{i \hbar}{2m} \left[CC^{*} e^{-\beta x} \frac{\partial e^{-\beta x}}{\partial x} - CC^{*} e^{-\beta x} \frac{\partial e^{-\beta x}}{\partial x} \right]$
$S_{t}= -\frac{i \hbar}{2m} \left[CC^{*} e^{-\beta x} (-\beta) e^{-\beta x} - CC^{*} e^{-\beta x} (-\beta) e^{-\beta x} \right]$
$S_{t}= -\frac{i \hbar}{2m} \left[-CC^{*} e^{-2\beta x} (\beta) + CC^{*} e^{-2\beta x} (\beta) \right]$
$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ From \: equation (3) \right\}$
$\psi_{1} (x) = A e^{ik_{1}x} + B e^{-ik_{1}x} \qquad \left\{ from \: eqaution \: (3) \right\}$
$\psi_{2} (x) = G e^{ i k_{2} \: x} \qquad \left\{ from \: eqaution \: (28) \right\}$
$S_{i} =(Incident \: wave \: function)(Complex \: conjugate \: of \: incident \: wave \: function) \frac{\hbar k_{1}}{m}$
$S_{r} =(Reflected \: wave \: function)(Complex \: conjugate \: of \: reflected \: wave \: function) \frac{\hbar k_{1}}{m}$
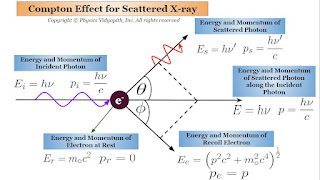
Description of Compton Effect : Experiment Setup, Theory, Theoretical Expression, Limitation, Recoil Electron
$p^{2}c^{2} + m_{\circ}^{2}c^{4} = h^{2} \left( \nu - \nu' \right)^{2} + m_{\circ}^{2}c^{4} + 2 h \left( \nu - \nu' \right) m_{\circ}c^{2}$
$\frac{p^{2}c^{2}}{h^{2}}\: cos^{2}\phi + \frac{p^{2}c^{2}}{h^{2}}\: sin^{2}\phi = \left(\nu - \nu'\: cos\theta \right)^{2}+ \nu'^{2}\: sin^{2}\theta $
$\frac{p^{2}c^{2}}{h^{2}} \left(sin^{2}\phi + cos^{2}\phi \right) = \left(\nu - \nu'\: cos\theta \right)^{2}+ \nu'^{2}\: sin^{2}\theta $
$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2}\: cos^{2}\theta - 2 \nu \nu' \:cos\theta + \nu'^{2}\: sin^{2}\theta $
$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2} \left(sin^{2}\theta + cos^{2}\theta \right) - 2 \nu \nu' \:cos\theta $
$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2} - 2 \nu \nu'+ 2 \nu \nu' - 2 \nu \nu' \:cos\theta $
$ \left( \nu - \nu' \right)^{2} + \frac{2m_{\circ}c^{2}}{h} \left( \nu - \nu' \right) = \left(\nu - \nu' \right)^{2} + 2 \nu \nu'\left(1 - cos\theta \right)$
$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} sec^{2}\phi - \left( 1 + \alpha \right)^{2}$
$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} sec^{2}\phi - \left( 1 + \alpha^{2}+ 2\alpha \right)$
$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} sec^{2}\phi - 1 - \alpha^{2} - 2\alpha $
Inadequacy of classical mechanics
Classical mechanics is a branch of physics that deals with the motion of macroscopic bodies or objects $(i.e \: the \: size \: range \: greater \: then \: 10^{-8}m)$ under the influence of forces. While it was groundbreaking when first developed by Sir Isaac Newton in the 17th century, it has certain limitations that were discovered over time. In this answer, we will discuss these limitations in more detail:
- Classical Mechanics is not applicable to extremely small objects: Classical mechanics assumes that particles have a definite position and momentum, which is not true in the quantum world. This limitation became apparent in the early 20th century with the discovery of quantum mechanics. Quantum mechanics is a branch of physics that deals with the behavior or motion of particles on an atomic and subatomic level $(i.e \: the \: size \: range \: is \: in \: between \: 10^{-8}m \: to \: 10^{-15}m)$ i.e microscopic particles. It has been successful in explaining phenomena such as the photoelectric effect, blackbody radiation, and the behavior of electrons in atoms, which cannot be explained by classical mechanics.
- Classical Mechanics is not applicable to objects moving at very high speeds: Classical mechanics assumes that the speed of an object can be infinite, it is not true in the relativistic world. The theory of relativity which was developed by Albert Einstein in the early 20th century, explains the behavior of objects moving at high speeds (i.e. equal to the speed of light). The theory of relativity has been successful in predicting phenomena such as time dilation, length contraction, and the equivalence of mass and energy.
- Classical Mechanics can not well explain the behavior of systems with many particles: Classical mechanics is not well suited for dealing with systems that have many particles. This is because it is difficult to solve the equations of motion for systems with many particles, and the behavior of the system can become chaotic. The theory of statistical mechanics, developed in the late 19th century, addresses this limitation by using probability distributions to describe the behavior of large systems.
- Classical Mechanics can not explain the behavior of objects that are very far apart or have very high masses: Newton's law of gravity works well for objects that are close together, but it fails to explain the behavior of objects that are extremely far apart or have very high masses, such as black holes and galaxies. The theory of general relativity, developed by Einstein in the early 20th century, provides a better explanation of the behavior of objects with very high masses and gravitational fields.
- Classical Mechanics assumes determinism: Classical mechanics assumes that the universe is deterministic, meaning that the future state of a system can be predicted with complete accuracy if the initial state is known. However, this assumption has been challenged by the theory of chaos, which suggests that small changes in the initial state of a system can lead to unpredictable and chaotic behavior in the future.
Intensity of a wave
Definition of Intensity of a wave:
If the energy $E$ is delivered in the time $t$ rom area $A$ perpendicular to the wave propagation, then
$I=\frac{E}{At} \qquad{1}$
Unit: $Joule/m^{2}-sec$ or $watt/m^{2}$
Dimensional formula: $[MT^{-3}]$
We know that the total mechanical energy of a vibrating particle is
$E=\frac{1}{2}m \omega^{2} a^{2}$
Where $\omega$ is the angular frequency and $a$ is the amplitude of the wave.
$E=\frac{1}{2}m (2\pi n)^{2} a^{2} \qquad \left( \omega=2\pi n \right)$
$E=2 \pi^{2} m n^{2} a^{2} \qquad(2)$
Where $m$ is the mass of the vibrating particle.
Now substitute the value of $E$ from equation $(2)$ to equation $(1)$. So the intensity of the wave
$I=\frac{2 \pi^{2} m n^{2} a^{2}}{At} \qquad(3)$
If the wave travels the distance $x$ in time $t$ with velocity $v$, Then
$t=\frac{x}{v}$
Now substitute the value of the above equation in equation $(3)$
$I=\frac{2 \pi^{2} m v n^{2} a^{2}}{Ax}$
$I=\frac{2 \pi^{2} m v n^{2} a^{2}}{V}$
Where $V$ is the volume of the corresponding medium during the wave propagation in time $t$.
$I=2 \pi^{2} \rho v n^{2} a^{2} \qquad \left(\because \rho=\frac{m}{V} \right)$
It is clear that for wave propagation in a medium with a constant velocity, i.e. wave's intensity is directly proportional to the square of amplitude and frequency both.
$I\propto a^{2}$ and $I \propto n^{2}$
In a medium, the energy per unit area per unit time delivered perpendicuar to the direction of the wave propagation s caled the intensity of the wave. It is denoted by $I$.
Difference between sound waves and light waves
Sound Waves:
Sound waves are mechanical waves in nature.
They need a medium to propagate and so cannot be produced in a vacuum.
They can move in all types of mediums as solid liquid or gas whether they are transparent or not.
They propagate in the form of longitudinal waves.
The particle of the medium vibrates along the direction of the propagation and so contraction and rarefaction are formed there.
These are three-dimensional waves.
These waves do not show a polarization effect.
For a normal human being the audible frequency range is $20$ to $20000 Hertz$.
The speed of the sound waves is more in a dense medium than in a rare medium.
Light waves:
light waves are electromagnetic waves in nature.
They don't need any medium and so can produce and propagate in a vacuum.
Their velocity in a vacuum is the maximum of value $3 \times 10^{8} m/s$
They can move in a transparent medium only.
They propagate in the form of transverse waves.
The electric field and magnetic field vibration are perpendicular to the direction of wave propagation.
These wave waves are also three-dimensional waves.
These waves source the polarization effect.
For a normal human being the visible frequency range is $4 \times 10^{18} Hz$ to $8 \times 10^{14} Hz$.
The speed of light is more in rare mediums than in dense ones.
Momentum wave function for a free particle
A non-relativistic free particle of mass $m$ moving in the positive $x$-direction with speed $v_{x}$ has kinetic energy
$E=\frac{1}{2} m v^{2}_{x}$
and momentum
$p_{x}=mv_{x}$
The energy and momentum are associated with a wave of wavelength $\lambda$ and frequency $\nu$ given by
$\lambda = \frac{h}{p_{x}}$
and
$\nu=\frac{E}{h}$
The propagation constant $k_{x}$ of the wave is
$k_{x}= \frac{2\pi}{\lambda}=\frac{2\pi}{\left(\frac{h}{p_{x}} \right)}=\frac{p_{x}}{\left(\frac{h}{2\pi} \right)}=\frac{p_{x}}{\hbar}$
and the angular frequency $\omega$ is
$\omega = 2\pi \nu = \frac{2\pi E}{\hbar}=\frac{E}{\hbar}$
A plane wave traveling along the $x$ axis in the positive direction may be represented by
$\psi(x,t)=A e^{-i\left(k_{x} \: x - \omega t\right)}$
Now subtitute the value of $\omega$ and $k_{x}$ in above equation then we get
$\psi(x,t)=A e^{i\left( \frac{p_{x}}{\hbar} \: x - \frac{E}{\hbar} \: t\right)}$
$\psi(x,t)=A e^{\frac{i}{\hbar}\left( p_{x} \: x - E \: t\right)}$
The superposition of a number of such waves of propagation number slightly different from an average value traveling simultaneously along the same line in the positive $x$- direction forms a wave packet of small extension. By Fourier's theorem the eave packet may be expressed by
The function $\psi(x,t)$ is called the momentum wave function for the motion of the free particle in one dimension.
The amplitude $A(p_{x})$ of the $x$-component of the momentum is given by the Fourier tranform
In three dimension the wave function is represented by
Where $d^{3}\overrightarrow{p}=dp_{x} \: dp_{y} \: dp_{z}$ is the volume element in the momentum space. In equation $(1)$, equation $(2)$ and equation $(3)$ $\frac{1}{\sqrt{2 \pi \hbar}}$ and $\frac{1}{(2 \pi \hbar)^{3/2}}$ are normalization constants.
$\psi(x,t) = \frac{1}{\sqrt{2 \pi \hbar}} \int_{-\infty}^{+\infty} A (p_{x}) e^{\frac{i}{\hbar}\left( p_{x} \: x - E \: t \right)} \: \: dp_{x} \qquad(1)$
$A(p)=\frac{1}{\sqrt{2 \pi \hbar}} \int_{-\infty}^{+\infty} \psi (x,t) e^{-\frac{i}{\hbar}\left( p_{x} \: x - E \: t \right)} \: \: dx \qquad(2)$
$\psi(\overrightarrow{r},t) = \frac{1}{(2 \pi \hbar)^{3/2}} \int_{-\infty}^{+\infty} A (\overrightarrow{p}) e^{\frac{i}{\hbar}\left( \overrightarrow{p} . \overrightarrow{r} - E \: t \right)} \: \: d^{3}\overrightarrow{p} \qquad(3)$
Schrodinger's equation for the complex conjugate waves function
Derivation:
The time dependent Schrodinger quation for the wave function function $psi(x,y,z,t)$ is
$-\frac{\hbar^{2}}{2m}\nabla^{2} \psi + V\psi=i\hbar\frac{\partial \psi}{\partial t} \qquad(1)$
Since wave function, $\psi$ is complex quantity i.e.
$\psi=\psi_{1}+i \: \psi_{2} \qquad(2)$
Where $\psi_{1}$ and $\psi_{2}$ are real functions of $x,y,z,t$. Substituting this form for $\psi$ in equation $(1)$, we get
$-\frac{\hbar^{2}}{2m}\nabla^{2} \left( \psi_{1}+i \: \psi_{2} \right) + V\left( \psi_{1}+i \: \psi_{2} \right)
\\ \qquad
= i\hbar\frac{\partial }{\partial t} \left( \psi_{1}+i \: \psi_{2} \right)$
Equation real and imaginary parts on either side of this equation, we obtain the following two equations:
$-\frac{\hbar^{2}}{2m}\nabla^{2} \psi_{1} + V\psi_{1}=-\hbar\frac{\partial \psi_{2}}{\partial t} \qquad(3)$
$-\frac{\hbar^{2}}{2m}\nabla^{2} \psi_{2} + V\psi_{2}=\hbar\frac{\partial \psi_{1}}{\partial t} \qquad(4)$
Mutiplying equation $(4)$ by $-i$ and adding it to equation $(3)$, we get
$-\frac{\hbar^{2}}{2m}\nabla^{2} \left( \psi_{1} - i \: \psi_{2} \right) + V\left( \psi_{1} - i \: \psi_{2} \right)
\\ \qquad
= -i\hbar\frac{\partial }{\partial t} \left( \psi_{1} - i \: \psi_{2} \right) \qquad(5)$
The complex conjugate of wave function $\psi^{*}$ is
$\psi^{*}=\psi^{*}_{1} - i \: \psi^{*}_{2} \qquad(6)$
Therefore, The equation $(5)$ can be written as
$-\frac{\hbar^{2}}{2m}\nabla^{2} \psi^{*} + V \psi^{*} =-i \hbar \frac{\partial \psi^{*}}{\partial t}$
This is the equation for complex conjugate wave function $\psi^{*}$.
Probability Current Density for a free particle in Quantum Mechanics
1.) Derivation of Probability Current Density for a free particle:
Let a particle of mass $m$ is moving in the positive $x$- direction in the region from $x_{1}$ to $x_{2}$.
For the one-dimensional motion of the particle, the wave function is $psi(x,t)$ Let $dA$ be the area of the cross-section of the region.
The probability of finding a particle in the region is
$\int_{x_{1}}^{x_{2}} \psi(x,t) \: \psi^{*}(x,t) \: dx \: dA \qquad(1)$
and the probability density of finding the particle in the region is
$P=\psi(x,t) \: \psi^{*}(x,t) \qquad(2)$
If the probability of finding the particle in the region decreases with time, the rate of decrease of the probability that the particle is in the region from $x_{1}$ to $x_{2}$ per unit area is called the probability current density out of the region. Therefore, the probability current density $S_{2} - S_{1}$ out of the region in the positive $x$-direction is given by
$S_{2} - S_{1} = - \frac{1}{dA} \left[- \frac{d}{dt} \int_{x_{1}}^{x_{2}} P \: dx \: dA \right]$
$S_{2} - S_{1} = - \frac{\partial}{\partial t} \int_{x_{1}}^{x_{2}} P \: dx $
$S_{2} - S_{1} = - \frac{\partial}{\partial t} \int_{x_{1}}^{x_{2}} \psi(x,t) \: \psi^{*}(x,t) \: dx \qquad(3)$
And the probability of current density at position $x$ is
$S = - \frac{\partial}{\partial t} \int \psi(x,t) \: \psi^{*}(x,t) \: dx \qquad(4)$
1.1) Show that: $S = \frac{i \hbar}{2m} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right]$
Proof:
According to the Schrodinger equation for wave function $\psi(x,t)$ and $\psi^{*}(x,t)$ are
$i \hbar \frac{\partial \psi}{\partial t} =- \frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi}{\partial x^{2}} + V \psi \qquad(1.1.1)$
The complex conjugate of the wave function
$-i \hbar \frac{\partial \psi^{*}}{\partial t} = -\frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi^{*}}{\partial x^{2}} + V \psi^{*} \qquad(1.1.2)$
Multiplying equation $(1.1.1)$ by $\psi^{*}$ and equation $(1.1.2)$ by $\psi$, we get
$i \hbar \psi^{*} \frac{\partial \psi}{\partial t} =- \frac{\hbar^{2}}{2m} \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} + \psi^{*} V \psi \quad(1.1.3)$
$-i \hbar \psi \frac{\partial \psi^{*}}{\partial t} = -\frac{\hbar^{2}}{2m} \psi \frac{\partial^{2} \psi^{*}}{\partial x^{2}} + \psi V \psi^{*} \quad(1.1.4)$
Now subtracting equation $(1.1.4)$ and equation $(1.1.3)$, we get
$i \hbar \left( \psi^{*} \frac{\partial \psi}{\partial t} + \psi \frac{\partial \psi^{*}}{\partial t} \right) =-\frac{\hbar^{2}}{2m} \left[ \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} - \psi \frac{\partial^{2} \psi^{*}}{\partial x^{2}} \right]$
$i \hbar \frac{\partial}{\partial t} \left( \psi \psi^{*} \right) =-\frac{\hbar^{2}}{2m} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right]$
$ \frac{\partial}{\partial t} \left( \psi \psi^{*} \right) =\frac{i\hbar}{2m} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right] \quad(1.1.5)$
We know that
$S = - \frac{\partial}{\partial t} \int \psi(x,t) \: \psi^{*}(x,t) \: dx $
Now substitute the value of equation $(9)$ in the above equation that can be written as
$ S = -\frac{i\hbar}{2m} \int \frac{\partial}{\partial x} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right] dx $
$ S = -\frac{i\hbar}{2m} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right] $
1.2) Show That The probability current density for a free particle is equal to the product of its probability density and its speed.
Proof:
For a free particle that is moving in the positive $x$-axis direction and the momentum $p_{x}$ at position $x$ is given by
$\frac{\hbar}{i} \frac{\partial \psi}{\partial x} = p_{x} \psi$
$ \frac{\partial \psi}{\partial x} = \frac{i}{\hbar} p_{x} \psi \qquad(1.2.1)$
and
$-\frac{\hbar}{i} \frac{\partial \psi^{*}}{\partial x} = p_{x} \psi^{*}$
$ \frac{\partial \psi^{*}}{\partial x} = - \frac{i}{\hbar} p_{x} \psi^{*} \qquad(1.2.2)$
We know that
$ S = -\frac{i\hbar}{2m} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right] $
Now substitute the value of equation $(1.2.1)$ and equation $(1.2.2)$ in the above equation, we get
$ S = -\frac{i\hbar}{2m} \left[ \psi^{*} \frac{i}{\hbar} p_{x} \psi + \psi \frac{i}{\hbar} p_{x} \psi^{*}\right] $
$ S = \frac{1}{2m} \left[ \psi^{*} p_{x} \psi + \psi p_{x} \psi^{*}\right] $
$ S = \frac{1}{m} \left( \psi \psi^{*} p_{x} \right)$
$ S = \frac{ p_{x} }{m} \left( \psi \psi^{*}\right) \qquad(1.2.3) $
Now put $p_{x}= m v_{x}$ in equation $(1.2.3)$
$ S = \frac{m v_{x} }{m} \left( \psi \psi^{*}\right)$
$ S = \left( \psi \psi^{*}\right) v_{x}$
Now put $p_{x}= \hbar k_{x}$ in equation $(1.2.3)$
$ S = \frac{ \hbar \: k_{x} }{m} \left( \psi \psi^{*}\right) $
Ehrenfest's Theorem and Derivation
Ehrenfest's Theorem Statement:
The theorem states that
Proof of theorem:
The proof of the theorem for one-dimensional motion of a particle by showing that
1) $\frac{d \left < x \right >}{dt} = \frac{\left < p_{x} \right > }{m}$
2) $\frac{d \left < p_{x} \right >}{dt} = \left < F_{x} \right >$
1.) To Show that: $\frac{d \left < x \right > }{dt} = \frac{\left < p_{x} \right > }{m}$
Let $x$ is the position coordinate of a particle of mass $m$, at time $t$
The expectation value of position $x$ of a particle is given by
$\left < x \right > = \int_{- \infty}^{+ \infty} \psi^{*} (x,t) . x \: \psi (x,t) dx \qquad (1)$
Differentiating the above equation $(1)$ with respect to $t$
$\frac{d \left < x \right > }{dt} = \int_{- \infty}^{+ \infty} x \frac{\partial (\psi \psi^{*})}{\partial t} dx \qquad(2)$
We know the probablity current density
$\frac{\partial (\psi \psi^{*})}{\partial t} = \frac{i \hbar}{2m} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right] \qquad(3)$
Now substitute the above eqaution$(3)$ in eqaution $(2)$
$\frac{d \left < x \right > }{dt} = \frac{i \hbar}{2m} \int_{- \infty}^{+ \infty} x \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right] dx $
Integrating the right-hand side by parts of the above equation, we get
$\frac{d \left < x \right > }{dt} = \frac{i \hbar}{2m} \left[ x \left( \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right) \right]^{+\infty}_{-\infty} \\
\qquad
- \frac{i \hbar}{2m} \int_{- \infty}^{+ \infty} \left( \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right) dx $
As $x$ approaches either $+ \infty$ or $-\infty$, $\psi$ and $\frac{\partial \psi}{\partial x}$ approach zero, and therefore the first term becomes zero.
Hence we get
$\frac{d \left < x \right > }{dt} = - \frac{i \hbar}{2m} \int_{- \infty}^{+ \infty} \left( \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right) dx
\\
\qquad\qquad\qquad\qquad\qquad\qquad ---(4)$
The expectation value of $p_{x}$ is given by
$ \left < p_{x} \right > = \int_{- \infty}^{+ \infty} \psi^{*} \frac{\hbar}{i} \frac{\partial \psi}{\partial x} $
$ \int_{- \infty}^{+ \infty} \psi^{*} \frac{\partial \psi}{\partial x} dx = \frac{i}{\hbar}\left < p_{x} \right > \qquad(5)$
Similarly
$ \int_{- \infty}^{+ \infty} \psi \frac{\partial \psi^{*}}{\partial x} dx = - \frac{i}{\hbar}\left < p_{x} \right > \qquad(6)$
Substituting the values of these integrals in equation $(4)$
$\frac{d \left < x \right > }{dt} = - \frac{i \hbar}{2m} \left[ \frac{i}{\hbar}\left < p_{x} \right > + \frac{i}{\hbar}\left < p_{x} \right >\right] $
$\frac{d \left < x \right > }{dt} = - \frac{\left < p_{x} \right >}{m} \qquad(7)$
This is the first result of Ehrenfest's Theorem.
2) To show that: $\frac{d \left < p_{x} \right >}{dt} = \left < F_{x} \right >$
We know that the expectation value of the momentum $p_{x}$ is given by
$ \left < p_{x} \right > = \int_{- \infty}^{+ \infty} \psi^{*} \frac{\hbar}{i} \frac{\partial \psi}{\partial x} $
$ \left < p_{x} \right > =\frac{\hbar}{i} \int_{- \infty}^{+ \infty} \psi^{*} \frac{\partial \psi}{\partial x} \qquad(8)$
Differentiating the equation $(8)$ with respect to $t$, we get
$\frac{d \left < p_{x} \right >}{dt} = \frac{\hbar}{i} \int_{- \infty}^{+ \infty} \left[ \frac{\partial \psi^{*}}{\partial t} \frac{\partial \psi}{\partial x} + \psi^{*} \frac{\partial^{2} \psi}{\partial x \partial t} \right] $
$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left[-i \hbar \frac{\partial \psi^{*}}{\partial t} \frac{\partial \psi}{\partial x} - i\hbar \psi^{*} \frac{\partial^{2} \psi}{\partial x \partial t} \right]
\\
\qquad\qquad\qquad\qquad\qquad\qquad ---(9)$
Now the time-dependent Schrodinger equations for $\psi$ and $\psi^{*}$ are
$i \hbar \frac{\partial \psi}{\partial t} =- \frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi}{\partial x^{2}} + V \psi \qquad(10)$
The complex conjugate of Schrodinger function
$-i \hbar \frac{\partial \psi^{*}}{\partial t} = -\frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi^{*}}{\partial x^{2}} + V \psi^{*} \qquad(11)$
Differentiating the equation $(10)$ with respect to $x$
$i \hbar \frac{\partial^{2} \psi}{\partial x \partial t} = - \frac{\hbar^{2}}{2m} \frac{\partial^{3} \psi}{\partial x^{3}} + \frac{\partial (V \psi)}{\partial x} \qquad(12)$
Now substitute the value of $-i \hbar \frac{\partial \psi^{*}}{\partial t}$ and $i \hbar \frac{\partial^{2} \psi}{\partial x \partial t}$ in the equation $(9)$, we get
Now put $\frac{\partial (V \psi)}{\partial x}= \left\{ \psi \frac{\partial V }{\partial x}+ V\frac{\partial \psi}{\partial x} \right\}$ in above equation:
$\frac{d \left < p_{x} \right >}{dt} = -\frac{\hbar^{2}}{2m} \int_{- \infty}^{+ \infty} \frac{\partial}{\partial x} \left( \frac{\partial \psi^{*}}{\partial x}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} \right) dx + \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \left\{ \psi \frac{\partial V }{\partial x}+ V\frac{\partial \psi}{\partial x} \right\} \right) dx$
As $x$ approaches either $+ \infty $ or $-\infty$ and $\frac{\partial \psi}{\partial x}$ is zero. Therefore the first term of the above equation on the right-hand side will be zero.
$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} - \psi \frac{\partial V }{\partial x} \psi^{*} dx$
$\frac{d \left < p_{x} \right >}{dt} = - \int_{- \infty}^{+ \infty} \psi \frac{\partial V }{\partial x} \psi^{*} dx$
$\frac{d \left < p_{x} \right >}{dt} = -\left < \frac{\partial V }{\partial x} \right > $
Here the $\left < \frac{\partial V }{\partial x} \right >$ is the average value or expectation value of potential gradient and the negative value of the potential gradient is equal to the average value or expectation value of force $\left < F_{x} \right >$ along the $x$ direction.
$\frac{d \left < p_{x} \right >}{dt} = \left < F_{x} \right > $
This is the second result of Ehrenfest theorem and it represents Newton's second law of motion. Thus if the expectation values of dynamical quantities for a particle are, considered, quantum mechanics given the equations of classical mechanics.
Quantum mechanics gives the same results as classical mechanics for a particle for which average or expectation values of dynamical quantities are involved.
$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left[ \left( -\frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi^{*}}{\partial x^{2}} + V \psi^{*} \right) \frac{\partial \psi}{\partial x} - \psi^{*} \left( - \frac{\hbar^{2}}{2m} \frac{\partial^{3} \psi}{\partial x^{3}} + \frac{\partial (V \psi)}{\partial x} \right) \right]$
$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left[-\frac{\hbar^{2}}{2m} \left( \frac{\partial^{2} \psi^{*}}{\partial x^{2}}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{3} \psi}{\partial x^{3}} \right) - \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial (V \psi)}{\partial x} \right) \right] dx$
$\frac{d \left < p_{x} \right >}{dt} = -\frac{\hbar^{2}}{2m} \int_{- \infty}^{+ \infty} \left( \frac{\partial^{2} \psi^{*}}{\partial x^{2}}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{3} \psi}{\partial x^{3}} \right) dx + \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial (V \psi)}{\partial x} \right) dx$
$\frac{d \left < p_{x} \right >}{dt} = -\frac{\hbar^{2}}{2m} \int_{- \infty}^{+ \infty} \frac{\partial}{\partial x} \left( \frac{\partial \psi^{*}}{\partial x}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} \right) dx + \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial (V \psi)}{\partial x} \right) dx$
$\frac{d \left < p_{x} \right >}{dt} = -\frac{\hbar^{2}}{2m} \left[ \frac{\partial \psi^{*}}{\partial x}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} \right]_{- \infty}^{+ \infty} + \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \left\{ \psi \frac{\partial V }{\partial x}+ V\frac{\partial \psi}{\partial x} \right\} \right) dx$
$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \left\{ \psi \frac{\partial V }{\partial x}+ V\frac{\partial \psi}{\partial x} \right\} \right) dx$
$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial V }{\partial x} \psi^{*} - V \psi^{*} \frac{\partial \psi}{\partial x} \right) dx$
Popular Posts
-
Angle of Acceptance → "If incident angle of light on the core for which the incident angle on the core-cladding interface equals t...
-
Let $S$ be a point monochromatic source of light of wavelength $\lambda$ placed at the focus of collimating lens $L_{1}$. The light beam is ...
-
Maxwell's Equations: Maxwell's equation of the electromagnetic wave is a collection of four equations i.e. Gauss's law of elec...
-
Derivation of interference of light due to a wedge-shaped thin film: Interference of light due to wedge-shaped thin film The wedge...
-
Let a plane wavefront be incident normally on slit $S_{1}$ and $S_{2}$ of equal $e$ and separated by an opaque distance $d$.The diffracted l...
Study-Material
Categories
Alternating Current Circuits
(10)
Atomic and Molecular Physics
(4)
Biomedical
(1)
Capacitors
(6)
Classical Mechanics
(12)
Current carrying loop in magnetic field
(5)
Current Electricity
(10)
Dielectric Materials
(1)
Electromagnetic Induction
(3)
Electromagnetic Wave Theory
(23)
Electrostatic
(22)
Energy Science and Engineering
(2)
Error and Measurement
(2)
Gravitation
(10)
Heat and Thermodynamics
(3)
Kinematics Theory Of Gases
(1)
Laser System & Application
(15)
Magnetic Effect of Current
(9)
Magnetic Substances
(3)
Mechanical Properties of Fluids
(4)
Nanoscience & Nanotechnology
(4)
Nuclear Physics
(7)
Numerical Problems and Solutions
(1)
Optical Fibre
(5)
Optics
(25)
Photoelectric Effect
(3)
Quantum Mechanics
(33)
Relativity
(8)
Semiconductors
(2)
Superconductors
(1)
Topic wise MCQ
(9)
Units and Dimensions
(1)
Waves
(5)