Description of Compton Effect : Experiment Setup, Theory, Theoretical Expression, Limitation, Recoil Electron

The Compton Effect

1	Compton Experiment Setup
2	Theory of the Compton Effect
3	Theoretical Derivation of Compton Effect (Equation of Compton Shift)
4	Limitation of Compton Effect
5	Compton Recoil Electron- 5(a)Relation between $\theta$ and $\phi$ 5(b) Kinetic Energy of the Recoil Electron

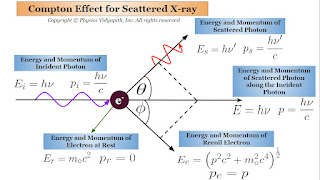
1.) Compton Experiment Setup:

The Compton effect is used to verify the particle nature of matter by applying the photoelectric effect. The setup of the Compton experiment as shown in the figure below which consists of the following parts

i.) X-ray source

ii.) Collimator

iii.) Target

iv.) Bragg's Spectrometer

i.) X-ray Source: The X-ray source is used to produce the monochromatic X-ray

ii.) Collimators: The collimators consist of slits that are used to pass the photon in the same direction.

iii.) Target: The target is made up of low atomic number material (i.e. Beryllium, Graphite, Aluminium) in which the monochromatic x-ray is incident and scattered in all directions.

iv.) Braggs Spectrometer: The Braggs spectrometer is used to measure the intensity of these scattered photons of monochromatic X-ray at different angles by the analyzing crystal and ionization chamber.

Working:

When the monochromatic X-ray is produced through an X-ray source and this monochromatic X-ray passes through slit $S_{1}$ and $S_{2}$ (i.e. Collimator). This slit $S_{1}$ and $S_{2}$ passes only the photon of a monochromatic X-ray beam in one direction. Now this beam is incident on graphite block (i.e. Target) and scattered in all directions. Now the intensity of the scattered beam at different angles is measured by a Braggs spectrometer. The major measured intensity by the Braggs spectrometer at different angles is shown in the figure below.

2.) Theory of the Compton Effect:

To explain the effect, Compton applied Einstein's quantum theory of light with the assumption that incident photons possess momentum. The postulates on which the theory is based are as follows.

i.) A beam of monochromatic X-ray is consist of a stream of photons having energy $h\nu$ and momentum $\frac{h\nu}{c}$. These photons travel in the direction of the beam with the speed of light.

ii.) The scattering of X-rays by atoms of graphite element is the result of elastic collisions between photons and electrons. This is an elastic collision so the energy and momentum will be conserved (i.e. in such a collision there is no loss of kinetic energy).

Note: The outer shell electron is loosely bound with the atom and required a very small amount of energy to leave the atom but the X-ray photons have very high energy. So the loosely bound electron of the atom leaves atom the permanently. Therefore for the X-ray loosely bound electrons can be considered as free electrons at rest.

3.) Theoretical Derivation of Compton Effect (Equation of Compton Shift):

Let us consider

The energy of the incident photon $E_{i}=h\nu$

The momentum of the incident photon $p_{i}=\frac{h\nu}{c}$

The energy of the scattered photon $E_{s}=h\nu'$

The momentum of the scattered photon $p_{s}=\frac{h\nu'}{c}$

The relativistic energy of the recoil electron $E_{e}=\left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right)^\frac{1}{2}$

The momentum of the recoil electron $p_{e}=p$

The energy of an electron at rest $E_{r}=m_{\circ}c^{2}$

The momentum of an electron at rest $p_{r}=0$

According to the energy conservation principle,

The total energy of an electron and an X-ray photon before the collision = The total energy of an electron and an X-ray photon after the collision

$E_{i}+E_{r}= E_{e}+E_{s}$

$h\nu + m_{\circ}c^{2} = \left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right)^\frac{1}{2} + h\nu'$

$\left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right)^\frac{1}{2} = h\nu - h\nu' + m_{\circ}c^{2}$

$\left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right)^\frac{1}{2} = h \left( \nu - \nu' \right) + m_{\circ}c^{2}$

Square the above equation

$\left( p^{2}c^{2} + m_{\circ}^{2}c^{4} \right) = \left[ h \left( \nu - \nu' \right) + m_{\circ}c^{2} \right]^{2}$

$p^{2}c^{2} + m_{\circ}^{2}c^{4} = h^{2} \left( \nu - \nu' \right)^{2} + m_{\circ}^{2}c^{4} + 2 h \left( \nu - \nu' \right) m_{\circ}c^{2}$

$p^{2}c^{2} = h^{2} \left( \nu - \nu' \right)^{2} + 2 h \left( \nu - \nu' \right) m_{\circ}c^{2}$

$\frac{p^{2}c^{2}}{h^{2}} = \left( \nu - \nu' \right)^{2} + \frac{2m_{\circ}c^{2}}{h} \left( \nu - \nu' \right) \qquad(1)$

Momentum is a vector quantity and it is conserved for elastic collision in each of two mutually perpendicular directions.

Total momentum along the direction of the incident photon:

$p\: cos\phi + \frac{h\nu'}{c} \: cos\theta=\frac{h\nu}{c}$

$p\: cos\phi =\frac{h\nu}{c} - \frac{h\nu'}{c} \: cos\theta$

$\frac{pc}{h}\: cos\phi =\nu - \nu'\: cos\theta \qquad(2)$

Total momentum at the right angle to the direction of the incident photon:

$p\:sin\phi=\frac{h\nu'}{c}sin\theta$

$\frac{pc}{h}\: sin\phi =\nu'\: sin\theta \qquad(3)$

To eliminate $\phi$, square the equation $(2)$ and equation $(3)$ and then add them. This gives

$\frac{p^{2}c^{2}}{h^{2}}\: cos^{2}\phi + \frac{p^{2}c^{2}}{h^{2}}\: sin^{2}\phi = \left(\nu - \nu'\: cos\theta \right)^{2}+ \nu'^{2}\: sin^{2}\theta $

$\frac{p^{2}c^{2}}{h^{2}} \left(sin^{2}\phi + cos^{2}\phi \right) = \left(\nu - \nu'\: cos\theta \right)^{2}+ \nu'^{2}\: sin^{2}\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \left(\nu - \nu'\: cos\theta \right)^{2}+ \nu'^{2}\: sin^{2}\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2}\: cos^{2}\theta - 2 \nu \nu' \:cos\theta + \nu'^{2}\: sin^{2}\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2} \left(sin^{2}\theta + cos^{2}\theta \right) - 2 \nu \nu' \:cos\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2} - 2 \nu \nu' \:cos\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \nu^{2} + \nu'^{2} - 2 \nu \nu'+ 2 \nu \nu' - 2 \nu \nu' \:cos\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \left(\nu - \nu' \right)^{2} + 2 \nu \nu' - 2 \nu \nu' \:cos\theta $

$\frac{p^{2}c^{2}}{h^{2}} = \left(\nu - \nu' \right)^{2} + 2 \nu \nu'\left(1 - cos\theta \right) \quad(4) $

Equation $(1)$ and equation $(4)$ left-hand sides are equal, So equate their right-hand sides, then we get

$ \left( \nu - \nu' \right)^{2} + \frac{2m_{\circ}c^{2}}{h} \left( \nu - \nu' \right) = \left(\nu - \nu' \right)^{2} + 2 \nu \nu'\left(1 - cos\theta \right)$

$ \frac{2m_{\circ}c^{2}}{h} \left( \nu - \nu' \right) = 2 \nu \nu'\left(1 - cos\theta \right)$

$ \frac{\left( \nu - \nu' \right)}{\nu\nu'} = \frac{h}{m_{\circ}c^{2}} \left(1 - cos\theta \right)$

$ \frac{1}{\nu'}-\frac{1}{\nu} = \frac{h}{m_{\circ}c^{2}} \left(1 - cos\theta \right) \qquad(5)$

$ \frac{c}{\nu'}-\frac{c}{\nu} = \frac{hc}{m_{\circ}c^{2}} \left(1 - cos\theta \right)$

$ \frac{c}{\nu'}-\frac{c}{\nu} = \frac{h}{m_{\circ}c} \left(1 - cos\theta \right)$

$ \lambda'-\lambda = \frac{h}{m_{\circ}c} \left(1 - cos\theta \right) $

$ \Delta \lambda = \lambda'-\lambda = \frac{h}{m_{\circ}c} \left(1 - cos\theta \right) \qquad(6)$

$ \Delta \lambda = \lambda'-\lambda = \frac{2h}{m_{\circ}c} cos^{2}\theta \qquad(7)$

Here the equation $(6)$ and equation $(7)$ is the expression for the Compton Shift in the wavelength of the X-rays, scattered by electrons in a low atomic number material.

The quantity $\frac{h}{2m_{\circ}c}$ is called the "Compton wavelength" of the electron and denoted by $\lambda_{e}$. The numerical value of $\frac{h}{2m_{\circ}c}$ is $0.2426 \times 10^{-11}$ or $0.02426 A^{\circ}$. Now substitute this value in the above equation $(6)$ and equation $(7)$. Therefore

$ \Delta \lambda = \lambda'-\lambda = \lambda_{e} \left(1 - cos\theta \right) \: A^{\circ}$

$ \Delta \lambda = \lambda'-\lambda = 0.02426 \left(1 - cos\theta \right) \: A^{\circ}$

$ \Delta \lambda = \lambda'-\lambda = 2 \lambda_{e} \: cos^{2}\theta \: A^{\circ}$

$ \Delta \lambda = \lambda'-\lambda = 0.04852 \: cos^{2}\theta \: A^{\circ}$

Thus, this theoretical expression derived by Compton is in excellent agreement with this experimental result.

The expression $\Delta \lambda$ leads to the following conclusion:

i.) The wavelength of the radiation scattered at different angles $\theta$ is always greater than the wavelength of the incident radiation.

ii.) The wavelength shifts $\Delta \lambda$ is independent of the wavelength of the incident X-ray, and at a fixed angle of scattering it is the same for all substances containing unbound electrons at rest.

iii.) The wavelength shift increases with the angle of scattering $\theta$ and it has a maximum value equal to $\frac{2h}{m_{\circ}c}$ when $\theta=180^{\circ}$.

4.) Limitation of Compton Effect:

i.) The Compton theory does not explain the presence of X-rays of the same wavelength in the scattered radiation, as the incident rays.

An explanation for this unmodified scattered radiation is as follows:

The incident X-ray photons collide with loosely bound outer electrons and also with tightly bound inner electrons of the atm. During a collision of a photon with tightly bound electrons, the electron is not detached from the atom. Consequently the entire atom recoils. In such a collision the Compton shift of the wavelength is given by replacing $m_{\circ}$ by the mass of the atom in equation $(7)$. Calculations show that this shift is so small that it can not be detected because the mass of an atom is usually several thousand times greater than the mass of the electron at rest.

For Example, The Graphite scattered the mass $M$ of the atom is

$M=12 \times 1840 \times m_{\circ}$

The maximum value of the Compton shift due to the collision of photons with bound electrons of graphite atoms is

$\Delta \lambda = \frac{2h}{Mc} \: sin^{2} \frac{\theta}{2}$

$\Delta \lambda = \frac{2}{12 \times 1840} \left( \frac{h}{m_{\circ}c} \right) \: sin^{2} \frac{180^{\circ}}{2}$

$\Delta \lambda = 9.058 \times 10^{-5} \times 0.02426 A^{\circ}$

$\Delta \lambda = 2.197 \times 10^{-6} A^{\circ}$

Thus the $\Delta \lambda$ is negligible.

ii.) It has been observed that the intensity of the modified X-rays is greater than that of unmodified X-rays for low atomic number materials. But for heavier materials i.e. high atomic number materials the reverse observation has been obtained. These results are not explained by the Compton theory.

5.) Compton Recoil Electron:

To study the direction $\phi$ of ejection of the recoil electron and its energy we derive the following expression

5(a) Relation between $\theta$ and $\phi$:

From the Compton theory, from equation $(5)$ we have

$ \frac{1}{\nu'}-\frac{1}{\nu} = \frac{h}{m_{\circ}c^{2}} \left(1 - cos\theta \right) $

$ \frac{\nu}{\nu'}-1 = \frac{h \nu}{m_{\circ}c^{2}} \left(1 - cos\theta \right) $

Let $\alpha =\frac{h \nu}{m_{\circ}c^{2}}$, then above equation can be written as

$ \frac{\nu}{\nu'}-1 = \alpha \left(1 - cos\theta \right) $

$ \frac{\nu}{\nu'} = 1 + \alpha \left(1 - cos\theta \right) \qquad(8) $

Now from equation $(2)$ and equation $(3)$

$\frac{pc}{h}\: cos\phi =\nu - \nu'\: cos\theta$

$\frac{pc}{h}\: sin\phi =\nu'\: sin\theta $

Now divide the above equation:

$cot\phi = \frac{\nu - \nu'\: cos\theta}{\nu'\: sin\theta}$

$cot\phi = \frac{1}{sin \theta} \left ( \frac{\nu}{\nu'} - cos \theta \right)$

Now substitute the value $\frac{\nu}{\nu'}$ form equation $(8)$ in above equation

$cot\phi = \frac{1}{sin \theta} \left[ 1 + \alpha \left(1 - cos\theta \right) - cos \theta \right]$

$cot\phi = \frac{\left( 1 + \alpha \right) \left( 1 - cos\theta \right)}{sin \theta}$

$cot\phi = \frac{\left( 1 + \alpha \right) \left( 2 sin^{2}\frac{\theta}{2} \right)}{2 sin \frac{\theta}{2} cos\frac{\theta}{2}} $

$cot\phi = \frac{\left( 1 + \alpha \right) \left( sin\frac{\theta}{2} \right)}{cos\frac{\theta}{2}} $

$cot\phi = \left( 1 + \alpha \right) tan\frac{\theta}{2} \qquad(9)$

This equation shows that the maximum value of $\phi=90^{\circ}$, when $\theta=0^{\circ}$. Therefore, the recoil electrons ejected at angles $\phi$ less than $90^{\circ}$.

5(b) Kinetic Energy of the Recoil Electron:

The kinetic energy of recoil electron $(E)$ is the difference between the kinetic energy of incident photon $(h\nu)$ and the kinetic energy of the scattered photon $(h\nu')$. i.e

$E=h\nu-h\nu' \qquad(10)$

Now from equation $(8)$

$ \frac{\nu}{\nu'} = 1 + \alpha \left(1 - cos\theta \right) $

$ \nu' = \frac{\nu}{1 + \alpha \left(1 - cos\theta \right)} $

Now subtitute the value of $\nu'$ in equation $(10)$, so we get

$E=h\nu-\frac{h \nu}{1 + \alpha \left(1 - cos\theta \right)}$

$E=h\nu \left[1-\frac{1}{1 + \alpha \left(1 - cos\theta \right)} \right]$

$E=h\nu \left[\frac{1 + \alpha \left(1 - cos\theta \right) -1}{1 + \alpha \left(1 - cos\theta \right)} \right]$

$E=h\nu \left[\frac{\alpha \left(1 - cos\theta \right)}{1 + \alpha \left(1 - cos\theta \right)} \right] \qquad(11)$

$E=h\nu \left[\frac{\alpha \left(2sin^{2}\frac{\theta}{2} \right)}{1 + \alpha \left(2sin^{2}\frac{\theta}{2} \right)} \right]$

$E=h\nu \left[\frac{2\alpha}{cosec^{2} \frac{\theta}{2} +2 \alpha} \right] \qquad(12)$

The right-hand side of the above equation can be expressed in terms of $\phi$. Now from equation $(9)$

$cot\phi = \left( 1 + \alpha \right) tan\frac{\theta}{2}$

$\frac{1}{tan \phi}= \left( 1 + \alpha \right) \frac{1}{cot \frac{\theta}{2}}$

$cot \frac{\theta}{2}= \left( 1 + \alpha \right) \: tan \phi $

Now squaring the above equation

$cot^{2} \frac{\theta}{2}= \left( 1 + \alpha \right)^{2} \: tan^{2} \phi $

$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} \left( sec^{2}\phi -1 \right) $

$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} sec^{2}\phi - \left( 1 + \alpha \right)^{2}$

$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} sec^{2}\phi - \left( 1 + \alpha^{2}+ 2\alpha \right)$

$cosec^{2} \frac{\theta}{2} - 1 = \left( 1 + \alpha \right)^{2} sec^{2}\phi - 1 - \alpha^{2} - 2\alpha $

$cosec^{2} \frac{\theta}{2} + 2\alpha = \left( 1 + \alpha \right)^{2} sec^{2}\phi - \alpha^{2} $

Now substitute the value of the above equation in equation $(12)$, then we get

$E=h\nu \left[\frac{2\alpha}{\left( 1 + \alpha \right)^{2} sec^{2}\phi - \alpha^{2}} \right] $

$E=h\nu \left[\frac{2\alpha \: cos^{2}\phi}{\left( 1 + \alpha \right)^{2} - \alpha^{2} \: cos^{2}\phi} \right] $

The experimental value of $E$ of recoil electrons determined by Compton and Simon in $1925$ and by Bless in $1927$ agreed well with the theoretical value.

The study of the Compton effect leads to the conclusion that radiant energy in its interaction with matter behaves as a stream of discrete particles (Photons) each having energy $h\nu$ and momentum $\frac{h\nu}{c}$. In other words, radiant energy is quantized. Therefore the Compton effect is considered a decisive phenomenon in support of the quantization of energy.

Read More

Inadequacy of classical mechanics

Classical mechanics is a branch of physics that deals with the motion of macroscopic bodies or objects $(i.e \: the \: size \: range \: greater \: then \: 10^{-8}m)$ under the influence of forces. While it was groundbreaking when first developed by Sir Isaac Newton in the 17th century, it has certain limitations that were discovered over time. In this answer, we will discuss these limitations in more detail:

1. Classical Mechanics is not applicable to extremely small objects: Classical mechanics assumes that particles have a definite position and momentum, which is not true in the quantum world. This limitation became apparent in the early 20th century with the discovery of quantum mechanics. Quantum mechanics is a branch of physics that deals with the behavior or motion of particles on an atomic and subatomic level $(i.e \: the \: size \: range \: is \: in \: between \: 10^{-8}m \: to \: 10^{-15}m)$ i.e microscopic particles. It has been successful in explaining phenomena such as the photoelectric effect, blackbody radiation, and the behavior of electrons in atoms, which cannot be explained by classical mechanics.
2. Classical Mechanics is not applicable to objects moving at very high speeds: Classical mechanics assumes that the speed of an object can be infinite,  it is not true in the relativistic world. The theory of relativity which was developed by Albert Einstein in the early 20th century, explains the behavior of objects moving at high speeds (i.e. equal to the speed of light). The theory of relativity has been successful in predicting phenomena such as time dilation, length contraction, and the equivalence of mass and energy.
3. Classical Mechanics can not well explain the behavior of systems with many particles: Classical mechanics is not well suited for dealing with systems that have many particles. This is because it is difficult to solve the equations of motion for systems with many particles, and the behavior of the system can become chaotic. The theory of statistical mechanics, developed in the late 19th century, addresses this limitation by using probability distributions to describe the behavior of large systems.
4. Classical Mechanics can not explain the behavior of objects that are very far apart or have very high masses: Newton's law of gravity works well for objects that are close together, but it fails to explain the behavior of objects that are extremely far apart or have very high masses, such as black holes and galaxies. The theory of general relativity, developed by Einstein in the early 20th century, provides a better explanation of the behavior of objects with very high masses and gravitational fields.
5. Classical Mechanics assumes determinism: Classical mechanics assumes that the universe is deterministic, meaning that the future state of a system can be predicted with complete accuracy if the initial state is known. However, this assumption has been challenged by the theory of chaos, which suggests that small changes in the initial state of a system can lead to unpredictable and chaotic behavior in the future.

In summary, while classical mechanics is still useful for understanding the behavior of macroscopic objects, its limitations have led to the development of new theories, such as quantum mechanics, relativity, statistical mechanics, and chaos theory, which can explain the behavior of the universe at different scales and levels of complexity.

Read More

Intensity of a wave

Definition of Intensity of a wave:

In a medium, the energy per unit area per unit time delivered perpendicuar to the direction of the wave propagation s caled the intensity of the wave. It is denoted by $I$.

If the energy $E$ is delivered in the time $t$ rom area $A$ perpendicular to the wave propagation, then

$I=\frac{E}{At} \qquad{1}$

Unit: $Joule/m^{2}-sec$ or $watt/m^{2}$

Dimensional formula: $[MT^{-3}]$

We know that the total mechanical energy of a vibrating particle is

$E=\frac{1}{2}m \omega^{2} a^{2}$

Where $\omega$ is the angular frequency and $a$ is the amplitude of the wave.

$E=\frac{1}{2}m (2\pi n)^{2} a^{2} \qquad \left( \omega=2\pi n \right)$

$E=2 \pi^{2} m n^{2} a^{2} \qquad(2)$

Where $m$ is the mass of the vibrating particle.

Now substitute the value of $E$ from equation $(2)$ to equation $(1)$. So the intensity of the wave

$I=\frac{2 \pi^{2} m n^{2} a^{2}}{At} \qquad(3)$

If the wave travels the distance $x$ in time $t$ with velocity $v$, Then

$t=\frac{x}{v}$

Now substitute the value of the above equation in equation $(3)$

$I=\frac{2 \pi^{2} m v n^{2} a^{2}}{Ax}$

$I=\frac{2 \pi^{2} m v n^{2} a^{2}}{V}$

Where $V$ is the volume of the corresponding medium during the wave propagation in time $t$.

$I=2 \pi^{2} \rho v n^{2} a^{2} \qquad \left(\because \rho=\frac{m}{V} \right)$

It is clear that for wave propagation in a medium with a constant velocity, i.e. wave's intensity is directly proportional to the square of amplitude and frequency both.

$I\propto a^{2}$ and $I \propto n^{2}$

Read More

Difference between sound waves and light waves

Sound Waves:

Sound waves are mechanical waves in nature.

They need a medium to propagate and so cannot be produced in a vacuum.

They can move in all types of mediums as solid liquid or gas whether they are transparent or not.

They propagate in the form of longitudinal waves.

The particle of the medium vibrates along the direction of the propagation and so contraction and rarefaction are formed there.

These are three-dimensional waves.

These waves do not show a polarization effect.

For a normal human being the audible frequency range is $20$ to $20000 Hertz$.

The speed of the sound waves is more in a dense medium than in a rare medium.

Light waves:

light waves are electromagnetic waves in nature.

They don't need any medium and so can produce and propagate in a vacuum.

Their velocity in a vacuum is the maximum of value $3 \times 10^{8} m/s$

They can move in a transparent medium only.

They propagate in the form of transverse waves.

The electric field and magnetic field vibration are perpendicular to the direction of wave propagation.

These wave waves are also three-dimensional waves.

These waves source the polarization effect.

For a normal human being the visible frequency range is $4 \times 10^{18} Hz$ to $8 \times 10^{14} Hz$.

The speed of light is more in rare mediums than in dense ones.

Read More

Momentum wave function for a free particle

A non-relativistic free particle of mass $m$ moving in the positive $x$-direction with speed $v_{x}$ has kinetic energy

$E=\frac{1}{2} m v^{2}_{x}$

and momentum

$p_{x}=mv_{x}$

The energy and momentum are associated with a wave of wavelength $\lambda$ and frequency $\nu$ given by

$\lambda = \frac{h}{p_{x}}$

and

$\nu=\frac{E}{h}$

The propagation constant $k_{x}$ of the wave is

$k_{x}= \frac{2\pi}{\lambda}=\frac{2\pi}{\left(\frac{h}{p_{x}} \right)}=\frac{p_{x}}{\left(\frac{h}{2\pi} \right)}=\frac{p_{x}}{\hbar}$

and the angular frequency $\omega$ is

$\omega = 2\pi \nu = \frac{2\pi E}{\hbar}=\frac{E}{\hbar}$

A plane wave traveling along the $x$ axis in the positive direction may be represented by

$\psi(x,t)=A e^{-i\left(k_{x} \: x - \omega t\right)}$

Now subtitute the value of $\omega$ and $k_{x}$ in above equation then we get

$\psi(x,t)=A e^{i\left( \frac{p_{x}}{\hbar} \: x - \frac{E}{\hbar} \: t\right)}$

$\psi(x,t)=A e^{\frac{i}{\hbar}\left( p_{x} \: x - E \: t\right)}$

The superposition of a number of such waves of propagation number slightly different from an average value traveling simultaneously along the same line in the positive $x$- direction forms a wave packet of small extension. By Fourier's theorem the eave packet may be expressed by

$\psi(x,t) = \frac{1}{\sqrt{2 \pi \hbar}} \int_{-\infty}^{+\infty} A (p_{x}) e^{\frac{i}{\hbar}\left( p_{x} \: x - E \: t \right)} \: \: dp_{x} \qquad(1)$

The function $\psi(x,t)$ is called the momentum wave function for the motion of the free particle in one dimension.

The amplitude $A(p_{x})$ of the $x$-component of the momentum is given by the Fourier tranform

$A(p)=\frac{1}{\sqrt{2 \pi \hbar}} \int_{-\infty}^{+\infty} \psi (x,t) e^{-\frac{i}{\hbar}\left( p_{x} \: x - E \: t \right)} \: \: dx \qquad(2)$

In three dimension the wave function is represented by

$\psi(\overrightarrow{r},t) = \frac{1}{(2 \pi \hbar)^{3/2}} \int_{-\infty}^{+\infty} A (\overrightarrow{p}) e^{\frac{i}{\hbar}\left( \overrightarrow{p} . \overrightarrow{r} - E \: t \right)} \: \: d^{3}\overrightarrow{p} \qquad(3)$

Where $d^{3}\overrightarrow{p}=dp_{x} \: dp_{y} \: dp_{z}$ is the volume element in the momentum space. In equation $(1)$, equation $(2)$ and equation $(3)$ $\frac{1}{\sqrt{2 \pi \hbar}}$ and $\frac{1}{(2 \pi \hbar)^{3/2}}$ are normalization constants.

Read More

Schrodinger's equation for the complex conjugate waves function

Derivation:

The time dependent Schrodinger quation for the wave function function $psi(x,y,z,t)$ is

$-\frac{\hbar^{2}}{2m}\nabla^{2} \psi + V\psi=i\hbar\frac{\partial \psi}{\partial t} \qquad(1)$

Since wave function, $\psi$ is complex quantity i.e.

$\psi=\psi_{1}+i \: \psi_{2} \qquad(2)$

Where $\psi_{1}$ and $\psi_{2}$ are real functions of $x,y,z,t$. Substituting this form for $\psi$ in equation $(1)$, we get

$-\frac{\hbar^{2}}{2m}\nabla^{2} \left( \psi_{1}+i \: \psi_{2} \right) + V\left( \psi_{1}+i \: \psi_{2} \right) \\ \qquad = i\hbar\frac{\partial }{\partial t} \left( \psi_{1}+i \: \psi_{2} \right)$

Equation real and imaginary parts on either side of this equation, we obtain the following two equations:

$-\frac{\hbar^{2}}{2m}\nabla^{2} \psi_{1} + V\psi_{1}=-\hbar\frac{\partial \psi_{2}}{\partial t} \qquad(3)$

$-\frac{\hbar^{2}}{2m}\nabla^{2} \psi_{2} + V\psi_{2}=\hbar\frac{\partial \psi_{1}}{\partial t} \qquad(4)$

Mutiplying equation $(4)$ by $-i$ and adding it to equation $(3)$, we get

$-\frac{\hbar^{2}}{2m}\nabla^{2} \left( \psi_{1} - i \: \psi_{2} \right) + V\left( \psi_{1} - i \: \psi_{2} \right) \\ \qquad = -i\hbar\frac{\partial }{\partial t} \left( \psi_{1} - i \: \psi_{2} \right) \qquad(5)$

The complex conjugate of wave function $\psi^{*}$ is

$\psi^{*}=\psi^{*}_{1} - i \: \psi^{*}_{2} \qquad(6)$

Therefore, The equation $(5)$ can be written as

$-\frac{\hbar^{2}}{2m}\nabla^{2} \psi^{*} + V \psi^{*} =-i \hbar \frac{\partial \psi^{*}}{\partial t}$

This is the equation for complex conjugate wave function $\psi^{*}$.

Read More

Probability Current Density for a free particle in Quantum Mechanics

1.) Derivation of Probability Current Density for a free particle:

Let a particle of mass $m$ is moving in the positive $x$- direction in the region from $x_{1}$ to $x_{2}$.

For the one-dimensional motion of the particle, the wave function is $psi(x,t)$ Let $dA$ be the area of the cross-section of the region.

The probability of finding a particle in the region is

$\int_{x_{1}}^{x_{2}} \psi(x,t) \: \psi^{*}(x,t) \: dx \: dA \qquad(1)$

and the probability density of finding the particle in the region is

$P=\psi(x,t) \: \psi^{*}(x,t) \qquad(2)$

If the probability of finding the particle in the region decreases with time, the rate of decrease of the probability that the particle is in the region from $x_{1}$ to $x_{2}$ per unit area is called the probability current density out of the region. Therefore, the probability current density $S_{2} - S_{1}$ out of the region in the positive $x$-direction is given by

$S_{2} - S_{1} = - \frac{1}{dA} \left[- \frac{d}{dt} \int_{x_{1}}^{x_{2}} P \: dx \: dA \right]$

$S_{2} - S_{1} = - \frac{\partial}{\partial t} \int_{x_{1}}^{x_{2}} P \: dx $

$S_{2} - S_{1} = - \frac{\partial}{\partial t} \int_{x_{1}}^{x_{2}} \psi(x,t) \: \psi^{*}(x,t) \: dx \qquad(3)$

And the probability of current density at position $x$ is

$S = - \frac{\partial}{\partial t} \int \psi(x,t) \: \psi^{*}(x,t) \: dx \qquad(4)$

1.1) Show that: $S = \frac{i \hbar}{2m} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right]$

Proof:

According to the Schrodinger equation for wave function $\psi(x,t)$ and $\psi^{*}(x,t)$ are

$i \hbar \frac{\partial \psi}{\partial t} =- \frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi}{\partial x^{2}} + V \psi \qquad(1.1.1)$

The complex conjugate of the wave function

$-i \hbar \frac{\partial \psi^{*}}{\partial t} = -\frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi^{*}}{\partial x^{2}} + V \psi^{*} \qquad(1.1.2)$

Multiplying equation $(1.1.1)$ by $\psi^{*}$ and equation $(1.1.2)$ by $\psi$, we get

$i \hbar \psi^{*} \frac{\partial \psi}{\partial t} =- \frac{\hbar^{2}}{2m} \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} + \psi^{*} V \psi \quad(1.1.3)$

$-i \hbar \psi \frac{\partial \psi^{*}}{\partial t} = -\frac{\hbar^{2}}{2m} \psi \frac{\partial^{2} \psi^{*}}{\partial x^{2}} + \psi V \psi^{*} \quad(1.1.4)$

Now subtracting equation $(1.1.4)$ and equation $(1.1.3)$, we get

$i \hbar \left( \psi^{*} \frac{\partial \psi}{\partial t} + \psi \frac{\partial \psi^{*}}{\partial t} \right) =-\frac{\hbar^{2}}{2m} \left[ \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} - \psi \frac{\partial^{2} \psi^{*}}{\partial x^{2}} \right]$

$i \hbar \frac{\partial}{\partial t} \left( \psi \psi^{*} \right) =-\frac{\hbar^{2}}{2m} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right]$

$ \frac{\partial}{\partial t} \left( \psi \psi^{*} \right) =\frac{i\hbar}{2m} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right] \quad(1.1.5)$

We know that

$S = - \frac{\partial}{\partial t} \int \psi(x,t) \: \psi^{*}(x,t) \: dx $

Now substitute the value of equation $(9)$ in the above equation that can be written as

$ S = -\frac{i\hbar}{2m} \int \frac{\partial}{\partial x} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right] dx $

$ S = -\frac{i\hbar}{2m} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right] $

1.2) Show That The probability current density for a free particle is equal to the product of its probability density and its speed.

Proof:

For a free particle that is moving in the positive $x$-axis direction and the momentum $p_{x}$ at position $x$ is given by

$\frac{\hbar}{i} \frac{\partial \psi}{\partial x} = p_{x} \psi$

$ \frac{\partial \psi}{\partial x} = \frac{i}{\hbar} p_{x} \psi \qquad(1.2.1)$

and

$-\frac{\hbar}{i} \frac{\partial \psi^{*}}{\partial x} = p_{x} \psi^{*}$

$ \frac{\partial \psi^{*}}{\partial x} = - \frac{i}{\hbar} p_{x} \psi^{*} \qquad(1.2.2)$

We know that

$ S = -\frac{i\hbar}{2m} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*}}{\partial x} \right] $

Now substitute the value of equation $(1.2.1)$ and equation $(1.2.2)$ in the above equation, we get

$ S = -\frac{i\hbar}{2m} \left[ \psi^{*} \frac{i}{\hbar} p_{x} \psi + \psi \frac{i}{\hbar} p_{x} \psi^{*}\right] $

$ S = \frac{1}{2m} \left[ \psi^{*} p_{x} \psi + \psi p_{x} \psi^{*}\right] $

$ S = \frac{1}{m} \left( \psi \psi^{*} p_{x} \right)$

$ S = \frac{ p_{x} }{m} \left( \psi \psi^{*}\right) \qquad(1.2.3) $

Now put $p_{x}= m v_{x}$ in equation $(1.2.3)$

$ S = \frac{m v_{x} }{m} \left( \psi \psi^{*}\right)$

$ S = \left( \psi \psi^{*}\right) v_{x}$

Now put $p_{x}= \hbar k_{x}$ in equation $(1.2.3)$

$ S = \frac{ \hbar \: k_{x} }{m} \left( \psi \psi^{*}\right) $

Read More

Ehrenfest's Theorem and Derivation

Ehrenfest's Theorem Statement:

The theorem states that

Quantum mechanics gives the same results as classical mechanics for a particle for which average or expectation values of dynamical quantities are involved.

Proof of theorem:

The proof of the theorem for one-dimensional motion of a particle by showing that

1) $\frac{d \left < x \right >}{dt} = \frac{\left < p_{x} \right > }{m}$

2) $\frac{d \left < p_{x} \right >}{dt} = \left < F_{x} \right >$

1.) To Show that: $\frac{d \left < x \right > }{dt} = \frac{\left < p_{x} \right > }{m}$

Let $x$ is the position coordinate of a particle of mass $m$, at time $t$

The expectation value of position $x$ of a particle is given by

$\left < x \right > = \int_{- \infty}^{+ \infty} \psi^{*} (x,t) . x \: \psi (x,t) dx \qquad (1)$

Differentiating the above equation $(1)$ with respect to $t$

$\frac{d \left < x \right > }{dt} = \int_{- \infty}^{+ \infty} x \frac{\partial (\psi \psi^{*})}{\partial t} dx \qquad(2)$

We know the probablity current density

$\frac{\partial (\psi \psi^{*})}{\partial t} = \frac{i \hbar}{2m} \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right] \qquad(3)$

Now substitute the above eqaution$(3)$ in eqaution $(2)$

$\frac{d \left < x \right > }{dt} = \frac{i \hbar}{2m} \int_{- \infty}^{+ \infty} x \frac{\partial}{\partial x} \left[ \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right] dx $

Integrating the right-hand side by parts of the above equation, we get

$\frac{d \left < x \right > }{dt} = \frac{i \hbar}{2m} \left[ x \left( \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right) \right]^{+\infty}_{-\infty} \\ \qquad - \frac{i \hbar}{2m} \int_{- \infty}^{+ \infty} \left( \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right) dx $

As $x$ approaches either $+ \infty$ or $-\infty$, $\psi$ and $\frac{\partial \psi}{\partial x}$ approach zero, and therefore the first term becomes zero.

Hence we get

$\frac{d \left < x \right > }{dt} = - \frac{i \hbar}{2m} \int_{- \infty}^{+ \infty} \left( \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial \psi^{*} }{\partial x} \right) dx \\ \qquad\qquad\qquad\qquad\qquad\qquad ---(4)$

The expectation value of $p_{x}$ is given by

$ \left < p_{x} \right > = \int_{- \infty}^{+ \infty} \psi^{*} \frac{\hbar}{i} \frac{\partial \psi}{\partial x} $

$ \int_{- \infty}^{+ \infty} \psi^{*} \frac{\partial \psi}{\partial x} dx = \frac{i}{\hbar}\left < p_{x} \right > \qquad(5)$

Similarly

$ \int_{- \infty}^{+ \infty} \psi \frac{\partial \psi^{*}}{\partial x} dx = - \frac{i}{\hbar}\left < p_{x} \right > \qquad(6)$

Substituting the values of these integrals in equation $(4)$

$\frac{d \left < x \right > }{dt} = - \frac{i \hbar}{2m} \left[ \frac{i}{\hbar}\left < p_{x} \right > + \frac{i}{\hbar}\left < p_{x} \right >\right] $

$\frac{d \left < x \right > }{dt} = - \frac{\left < p_{x} \right >}{m} \qquad(7)$

This is the first result of Ehrenfest's Theorem.

2) To show that: $\frac{d \left < p_{x} \right >}{dt} = \left < F_{x} \right >$

We know that the expectation value of the momentum $p_{x}$ is given by

$ \left < p_{x} \right > = \int_{- \infty}^{+ \infty} \psi^{*} \frac{\hbar}{i} \frac{\partial \psi}{\partial x} $

$ \left < p_{x} \right > =\frac{\hbar}{i} \int_{- \infty}^{+ \infty} \psi^{*} \frac{\partial \psi}{\partial x} \qquad(8)$

Differentiating the equation $(8)$ with respect to $t$, we get

$\frac{d \left < p_{x} \right >}{dt} = \frac{\hbar}{i} \int_{- \infty}^{+ \infty} \left[ \frac{\partial \psi^{*}}{\partial t} \frac{\partial \psi}{\partial x} + \psi^{*} \frac{\partial^{2} \psi}{\partial x \partial t} \right] $

$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left[-i \hbar \frac{\partial \psi^{*}}{\partial t} \frac{\partial \psi}{\partial x} - i\hbar \psi^{*} \frac{\partial^{2} \psi}{\partial x \partial t} \right] \\ \qquad\qquad\qquad\qquad\qquad\qquad ---(9)$

Now the time-dependent Schrodinger equations for $\psi$ and $\psi^{*}$ are

$i \hbar \frac{\partial \psi}{\partial t} =- \frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi}{\partial x^{2}} + V \psi \qquad(10)$

The complex conjugate of Schrodinger function

$-i \hbar \frac{\partial \psi^{*}}{\partial t} = -\frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi^{*}}{\partial x^{2}} + V \psi^{*} \qquad(11)$

Differentiating the equation $(10)$ with respect to $x$

$i \hbar \frac{\partial^{2} \psi}{\partial x \partial t} = - \frac{\hbar^{2}}{2m} \frac{\partial^{3} \psi}{\partial x^{3}} + \frac{\partial (V \psi)}{\partial x} \qquad(12)$

Now substitute the value of $-i \hbar \frac{\partial \psi^{*}}{\partial t}$ and $i \hbar \frac{\partial^{2} \psi}{\partial x \partial t}$ in the equation $(9)$, we get

$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left[ \left( -\frac{\hbar^{2}}{2m} \frac{\partial^{2} \psi^{*}}{\partial x^{2}} + V \psi^{*} \right) \frac{\partial \psi}{\partial x} - \psi^{*} \left( - \frac{\hbar^{2}}{2m} \frac{\partial^{3} \psi}{\partial x^{3}} + \frac{\partial (V \psi)}{\partial x} \right) \right]$

$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left[-\frac{\hbar^{2}}{2m} \left( \frac{\partial^{2} \psi^{*}}{\partial x^{2}}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{3} \psi}{\partial x^{3}} \right) - \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial (V \psi)}{\partial x} \right) \right] dx$

$\frac{d \left < p_{x} \right >}{dt} = -\frac{\hbar^{2}}{2m} \int_{- \infty}^{+ \infty} \left( \frac{\partial^{2} \psi^{*}}{\partial x^{2}}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{3} \psi}{\partial x^{3}} \right) dx + \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial (V \psi)}{\partial x} \right) dx$

$\frac{d \left < p_{x} \right >}{dt} = -\frac{\hbar^{2}}{2m} \int_{- \infty}^{+ \infty} \frac{\partial}{\partial x} \left( \frac{\partial \psi^{*}}{\partial x}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} \right) dx + \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial (V \psi)}{\partial x} \right) dx$

Now put $\frac{\partial (V \psi)}{\partial x}= \left\{ \psi \frac{\partial V }{\partial x}+ V\frac{\partial \psi}{\partial x} \right\}$ in above equation:

$\frac{d \left < p_{x} \right >}{dt} = -\frac{\hbar^{2}}{2m} \int_{- \infty}^{+ \infty} \frac{\partial}{\partial x} \left( \frac{\partial \psi^{*}}{\partial x}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} \right) dx + \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \left\{ \psi \frac{\partial V }{\partial x}+ V\frac{\partial \psi}{\partial x} \right\} \right) dx$

$\frac{d \left < p_{x} \right >}{dt} = -\frac{\hbar^{2}}{2m} \left[ \frac{\partial \psi^{*}}{\partial x}\frac{\partial \psi}{\partial x} - \psi^{*} \frac{\partial^{2} \psi}{\partial x^{2}} \right]_{- \infty}^{+ \infty} + \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \left\{ \psi \frac{\partial V }{\partial x}+ V\frac{\partial \psi}{\partial x} \right\} \right) dx$

As $x$ approaches either $+ \infty $ or $-\infty$ and $\frac{\partial \psi}{\partial x}$ is zero. Therefore the first term of the above equation on the right-hand side will be zero.

$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi^{*} \left\{ \psi \frac{\partial V }{\partial x}+ V\frac{\partial \psi}{\partial x} \right\} \right) dx$

$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} \left( V \psi^{*} \frac{\partial \psi}{\partial x} - \psi \frac{\partial V }{\partial x} \psi^{*} - V \psi^{*} \frac{\partial \psi}{\partial x} \right) dx$

$\frac{d \left < p_{x} \right >}{dt} = \int_{- \infty}^{+ \infty} - \psi \frac{\partial V }{\partial x} \psi^{*} dx$

$\frac{d \left < p_{x} \right >}{dt} = - \int_{- \infty}^{+ \infty} \psi \frac{\partial V }{\partial x} \psi^{*} dx$

$\frac{d \left < p_{x} \right >}{dt} = -\left < \frac{\partial V }{\partial x} \right > $

Here the $\left < \frac{\partial V }{\partial x} \right >$ is the average value or expectation value of potential gradient and the negative value of the potential gradient is equal to the average value or expectation value of force $\left < F_{x} \right >$ along the $x$ direction.

$\frac{d \left < p_{x} \right >}{dt} = \left < F_{x} \right > $

This is the second result of Ehrenfest theorem and it represents Newton's second law of motion. Thus if the expectation values of dynamical quantities for a particle are, considered, quantum mechanics given the equations of classical mechanics.

Read More

Eigen value of the momentum of a particle in one dimension box or infinite potential well

Equation of eigen value of the momentum of a particle in one dimension box:

The eigen value of the momentum $P_{n}$ of a particle in one dimension box moving along the x-axis is given by

$P^{2}_{n} = 2 m E_{n}$

$P^{2}_{n} = 2 m \frac{n^{2} \pi^{2} \hbar^{2}}{2 m L^{2}} \qquad \left( \because E_{n}= \frac{n^{2} \pi^{2} \hbar^{2}}{2 m L^{2}} \right)$

$P^{2}_{n} = \frac{n^{2} \pi^{2} \hbar^{2}}{L^{2}}$

$P_{n} = \pm \frac{n \pi \hbar}{L}$

$P_{n} = \pm \frac{n h}{2L} \qquad \left( \hbar = \frac{h}{2 \pi} \right)$

The $\pm$ sign indicates that the particle is moving back and forth in the infinite potential box.

The above equation shows that eigen value of the momentum of the particle is discrete and the difference between the momentum corresponding to two consecutive energy levels is always constant and equal to $\frac{h}{2L}$

Read More

Electric field intensity due to uniformly charged solid sphere (Conducting and Non-conducting)

A.) Electric field intensity at different points in the field due to the uniformly charged solid conducting sphere:

Let us consider, A solid conducting sphere that has a radius $R$ and charge $+q$ is distributed on the surface of the sphere in a uniform manner. Now find the electric field intensity at different points due to the solid-charged conducting sphere. These different points are: 1.) Electric field intensity outside the solid conducting sphere
2.) Electric field intensity on the surface of the solid conducting sphere
3.) Electric field intensity inside the solid conducting sphere

1.) Electric field intensity outside the solid conducting sphere:

If $O$ is the center of solid conducting spherical then the electric field intensity outside of the sphere can be determined by the following steps →

1.) First, take the point $P$ outside the sphere
2.) Draw a spherical surface of radius r which passes through point $P$. This hypothetical surface is known as the Gaussian surface.
3.) Now take a small area $\overrightarrow {dA} $ around point $P$ on the Gaussian surface to find the electric flux passing through it.
4.) Now find the direction between the electric field vector and a small area vector.

Due to uniform charge distribution, the electric field intensity will be the same at every point on the Gaussian surface. So from the figure,

The direction of electric field intensity on the Gaussian surface is radially outward which is in the direction of the area vector of the Gaussian surface. i.e. ($\theta=0^{\circ}$). Here $\overrightarrow {dA}$ is a small area around point $P$ so the small electric flux $d\phi_{E}$ will pass through this small area $\overrightarrow {dA}$. so this flux can be found by applying Gauss's law in question given below:

$ d\phi_{E}= \overrightarrow {E}\cdot \overrightarrow{dA}$

$ d\phi_{E}= E\:dA\: cos\: 0^{\circ} \quad \left \{\because \theta=0^{\circ} \right \}$

$ d\phi_{E}= E\:dA \quad (1) \quad \left \{\because cos\:0^{\circ}=1 \right \}$

The electric flux passes through the entire Gaussian surface, So integrate the equation $(1)$ →

$ \oint d\phi_{E}= \oint E\:dA $

$\phi_{E}=\oint E\:dA\qquad (2)$

According to Gauss's law:

$ \phi_{E}=\frac{q}{\epsilon_{0}}\qquad (3)$

From equation $(2)$ and equation $(3)$, we can write as

$ \frac{q}{\epsilon_{0}}=\oint E\:dA$

$ \frac{q}{\epsilon_{0}}= E\oint dA$

Now substitute the area of the entire Gaussian spherical is $\oint {dA}=4\pi r^{2}$ in the above equation. So the above equation can be written as:

$ \frac{q}{\epsilon_{0}}= E(4\pi r^{2})$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}}$

From the above equation, we can conclude that the behavior of the electric field at the external point due to the uniformly charged solid conducting sphere is the same as the entire charge is placed at the center, point charge

If the surface charge density is $\sigma$, Then the total charge $q$ on the surface of a solid conducting sphere is→

$ q=4\pi R^{2}\: \sigma$

Substitute this value of charge $q$ in the above equation, so we can write the equation as:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{4\pi R^{2}\: \sigma}{r^{2}}$

$ E=\frac{\sigma}{\epsilon_{0}}\frac{R^{2}}{r^{2}}$

This equation describes the electric field intensity at the external point of the solid conducting sphere.

2.) Electric field intensity on the surface of the solid conducting sphere:

If point $P$ is placed on the surface of the solid conducting sphere i.e. ($r=R$). so electric field intensity on the surface of the solid conducting sphere can be found by putting $r=R$ in the formula of electric field intensity at the external point of the solid conducting sphere:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{R^{2}}$

$ E=\frac{\sigma}{\epsilon_{0}}$

3.) Electric field intensity inside the solid conducting sphere:

If point $P$ is placed inside the solid conducting sphere then electric field intensity will be zero because the charge is distributed uniformly on the surface of the solid sphere and there will not be any charge on the Gaussian surface. So the electric flux will be zero inside the solid sphere. i.e.

$ \phi_{E}=\oint E\:dA$

$ 0=E\oint dA \qquad\quad \left \{ \because \phi_{E}=0 \right \}$

$ E=0$

Electric field intensity distribution with distance for Conducting Solid Sphere:

Electric field intensity distribution with distance shows that the electric field is maximum on the surface of the sphere and zero inside the sphere. Electric field intensity distribution outside the sphere reduces with the distance according to $E=\frac{1}{r^{2}}$.

B.) Electric field intensity at different points in the field due to the uniformly charged solid non-conducting sphere:

Let us consider, A solid non-conducting sphere of radius R in which $+q$ charge is distributed uniformly in the entire volume of the sphere. So electric field intensity at a different point due to the solid charged non-conducting sphere:

1. Electric field intensity outside the solid non-conducting sphere
2. Electric field intensity on the surface of the solid non-conducting sphere
3. Electric field intensity inside the non-solid conducting sphere

1.) Electric field intensity outside the solid non-conducting sphere:

Let us consider, An external point $P$ which is at a distance $r$ from the center point $O$ of the sphere. The electric flux is radially outward in the sphere. So the direction of the electric field vector and the small area vector will be in the same direction i.e. ($\theta =0^{\circ}$). Here $\overrightarrow {dA}$ is a small area, the small amount of electric flux will pass through this area i.e. →

$ d\phi_{E}= \overrightarrow {E}\cdot \overrightarrow{dA}$

$ d\phi_{E}= E\:dA\: cos\: 0^{\circ} \quad \left \{\because \theta=0^{\circ} \right \}$

$ d\phi_{E}= E\:dA \qquad (1) \quad \left \{\because cos\:0^{\circ}=1 \right \}$

The electric flux passes through the entire Gaussian surface, So integrate the equation $(1)$ →

$ \phi_{E}=\oint E\:dA\qquad (2)$

According to Gauss's law:

$ \phi_{E}=\frac{q}{\epsilon_{0}}\qquad (3)$

From equation (1) and equation (2), we can write as

$ \frac{q}{\epsilon_{0}}=\oint E\:dA$

$ \frac{q}{\epsilon_{0}}= E\oint dA$

Now substitute the area of the entire Gaussian spherical surface is $\oint {dA}=4\pi r^{2}$ in the above equation. So the above equation can be written as:

$ \frac{q}{\epsilon_{0}}= E(4\pi r^{2})$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}}$

From the above equation, we can conclude that the behavior of the electric field at the external point due to the uniformly charged solid non-conducting sphere is the same as the point charge i.e. like the entire charge is placed at the center.

Since the sphere is a non-conductor so the charge is distributed in the entire volume of the sphere. So charge distribution can calculate by volume charge density →

$q=\frac{4}{3} \pi R^{3} \rho $

Substitute this value of charge $q$ in the above equation, so we can write the equation as:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{4\pi R^{3}\: \rho}{3r^{2}}$

$ E=\frac{\rho}{\epsilon_{0}}\frac{R^{3}}{3r^{2}}$

This equation describes the electric field intensity at the external point of the solid non-conducting sphere.

2.) Electric field intensity on the surface of the solid non-conducting sphere:

If point $P$ is placed on the surface of a solid non-conducting sphere i.e. ($r=R$). so electric field intensity on the surface of a solid non-conducting sphere can be found by putting $r=R$ in the formula of electric field intensity at the external point of the solid non-conducting sphere:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{R^{2}}$

$ E=\frac{\rho R}{3\epsilon_{0}}$

3.) Electric field intensity inside the solid non-conducting sphere:

If point $P$ is placed inside the sphere and the distance from the origin $O$ is $r$, the electric flux which is passing through the Gaussian surface

$ \phi_{E}= E.4\pi r^{2}$

Where $\phi_{E}=\frac{q'}{\epsilon_{0}}$

$ \frac{q'}{\epsilon_{0}}=E.4\pi r^{2}$

Where $q'$ is part of charge $q$ which is enclosed with Gaussian Surface

$ E=\frac{1}{4 \pi \epsilon_{0}} \frac{q'}{r^{2}} \qquad \qquad (4)$

The charge is distributed uniformly in the entire volume of the sphere so volume charge density $\rho$ will be the same as the entire solid sphere i.e.

$ \rho=\frac{q}{\frac{4}{3}\pi R^{3}}=\frac{q'}{\frac{4}{3}\pi r^{3}}$

$ \frac{q}{\frac{4}{3}\pi R^{3}}=\frac{q'}{\frac{4}{3}\pi r^{3}}$

$ q'=q\frac{r^{3}}{R^{3}}$

$ q'=q\left (\frac{r}{R} \right)^{3}$

Put the value of $q'$ in equation $(4)$, so

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{q}{r^{2}}\left(\frac{r}{R} \right)^{3}$

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{qr}{R^{3}}$

Where $q=\frac{4}{3} \pi R^{3} \rho $. So above equation can be written as:

$ E=\frac{1}{4\pi \epsilon_{0}}\frac{\frac{4}{3} \pi R^{3} \rho r}{R^{3}}$

$E=\frac{ \rho r}{3 \epsilon_{0}}$

Electric field intensity distribution with distance for non-conducting Solid Sphere:

Electric field intensity distribution with distance shows that the electric field is maximum on the surface of the sphere and zero at the center of the sphere. Electric field intensity distribution outside the sphere reduces with the distance according to $E=\frac{1}{r^{2}}$.

Read More

Derivation of Planck's Radiation Law

Derivation: Let $ N$ be the total number of Planck’s oscillators and $E$ be their total energy, then the average energy per Planck’s oscillator is

$ \overline{E}=\frac{E_{N}}{N} \qquad (1)$

Let there be $ N_{0}, N_{1} ,N_{2} ,N_{3},---N_{n}$ oscillator having energy $ E_{0}, E_{1}, E_{2}, -- E_{n}$ respectively.

According to Maxwell’s distribution, the number of oscillators in the $ n^{th}$ energy state is related to the number of oscillators in the ground state by

$ N_{n}=N _{0} e^{\tfrac{-nh\nu }{kt} }\qquad (2)$

Where $ n$ is a positive integer. So put $ n= 1,2,3,…….$. The above equation can be written for different energy states. i.e.

$ N_{1}= N _{0} e^{\tfrac{-h\nu }{kt} }$

$ N_{2}= N _{0} e^{\tfrac{-2h\nu }{kt} }$

$ N_{3}= N _{0} e^{\tfrac{-3h\nu }{kt} }$

$.............$

$.............$

So, the total number of Planck’s Oscillators –

$ N= N _{0} +N_{1}+N_{2}+N_{3}+.... N_{n}$

$ N= N _{0} + N_{0} e^{\tfrac{-h\nu }{kt}}+ N_{0} e^{\tfrac{-2h\nu }{kt}}+...+ N_{0}e^{\tfrac{-nh\nu }{kt}}$

$ N= N _{0}[1+e^{\tfrac{-h\nu }{kt}}+e^{\tfrac{-2h\nu }{kt}}+.... e^{\tfrac{-nh\nu }{kt}}] \qquad(3)$

Let $ x = e^{\frac{-h\nu }{kt}} \qquad (4) $

Then $ N = N_{0}[1+x+x^{2}+x^{3}+...+ x^{n}]$

$ N = \frac{N_{0}}{1-x} \qquad(5)$ [ from Binomial theorem]

Now the total energy of oscillators –

$ E_{N} = E_{0}N_{0}+ E_{1}N_{1}+ E_{2}N_{2}+...+ E_{n}N_{n}$

$ E_{N } = 0.N_{0}+ h\nu N_{0} e^{\tfrac{-h\nu }{kt}}+...+nh\nu N_{0} e^{\tfrac{-nh\nu }{kt}}$

$ E_{N } = N_{0}h\nu (e^{\tfrac{-h\nu }{kt}}+2e^{\tfrac{-2h\nu }{kt}}+...+ ne^{\tfrac{-nh\nu }{kt}})$

From equation $(4)$ put $ x = e^{\tfrac{-h\nu }{kt}}$ in above equation. i.e

$ E_{N } = N_{0}h\nu (x+2x^{2}+3x^{3}+...+nx^{n}) $

$ E_{N } = N_{0}h\nu x(1+2x+3x^{2}+....)$

$ E_{N } = \frac{N_{0}h\nu x}{(1-x)^{2}} \qquad(6)$ (from Bionomical theorem)

Now substituting the value of $N$ from equation $ (5)$ and $ E_{n}$ from equation $ (6)$  in equation $ (1)$ –

$ \overline{E}= \frac{\frac{N_{0}h\nu x}{(1-x)^{2}}}{\frac{N_{0}}{(1-x)}}$

$ \overline{E}= \frac{h\nu }{(\frac{1}{x}-1)}$

$ \overline{E}= \frac{h\nu }{e^{\tfrac{h\nu }{kt}}-1} \qquad(7)$

The number of oscillators per unit volume in wavelength range to $ ( \lambda + d\lambda )$ is $\frac{8\pi }{\lambda ^{4}} d\lambda$.

The energy per unit volume $ (E_{\lambda }d\lambda )$ in the wavelength range to $( \lambda +d\lambda ) $ is –

$ E_{\lambda}d\lambda = \frac{8\pi }{\lambda ^{4}}d\lambda \overline{E} \qquad(8)$

From equation $ (7)$ and $ (8)$ –

$ E_{\lambda}d\lambda = \frac{8\pi }{\lambda ^{4}}d\lambda \frac{h\nu }{(e^{\tfrac{h\nu}{kt}}-1)}$

$ E_{\lambda}d\lambda = \frac{8\pi hc}{\lambda ^{5}} \frac{d\lambda}{(e^{\tfrac{hc}{\lambda kt}}-1)}$

The above equation describes Planck’s radiation law and this law was able to thoroughly explain the black body radiation spectrum.

Wien’s Displacement law from Planck’s Radiation Law:

Planck’s radiation law gives the energy in wavelength region $ \lambda to \lambda +d\lambda $ as –

$ E_{\lambda}d \lambda = \frac{8\pi hc}{\lambda ^{5}}(\frac{1}{e^{\tfrac{hc}{\lambda kt}}-1})d\lambda \qquad(1)$

For shorter wavelength $ \lambda T$ will be small and hence

$ e^{\tfrac{hc}{\lambda kt}}> > 1$

Hence, for a small value of $\lambda T$ Planck’s formula reduces to -

$ E_{\lambda}d \lambda = \frac{8\pi hc}{\lambda ^{5}}(\frac{1}{e^{\tfrac{hc}{\lambda kt}}}) d\lambda$

$ E_{\lambda}d\lambda = \frac{8\pi hc}{\lambda ^{5}}e^{\tfrac{-hc}{\lambda kt}}d\lambda$

$E_{\lambda}d\lambda = A \lambda ^{-5} e^{\tfrac{-hc}{\lambda kt}}d\lambda$

Where $ A = 8\pi hc$

The above equation is Wien’s law of energy distribution verified by Planck radiation law.

Rayleigh-Jeans law from Planck’s Radiation Law:

According to Planck’s radiation law –

$ E_{\lambda}.d\lambda = \frac{8\pi hc}{\lambda ^{5}}\frac{1 }{e^{\tfrac{hc}{\lambda kt}}-1}.d\lambda$

For longer wavelength $ e^{\frac{hc}{\lambda kt}}$ is small and can be expanded as-

$ e^{\tfrac{hc}{\lambda kt}} = 1+\frac{hc}{\lambda kt}+\frac{1}{2!}(\frac{hc}{\lambda kt})^{2}+....$

Neglecting the higher-order term –

$ e^{\tfrac{hc}{\lambda kt}} = 1+\frac{hc}{\lambda kt}$

Hence for longer wavelength, Planck’s formula reduces to –

$ E_{\lambda}.d\lambda = \frac{8\pi kt}{\lambda ^{5}}[\frac{1}{1+\frac{hc}{\lambda kt}-1}]$

$ E_{\lambda}.d\lambda = \frac{8\pi kt}{\lambda ^{4}}.d\lambda$

This is Rayleigh Jean’s law verified by Planck Radiation Law.

Read More

Orthogonality of the wave functions of a particle in one dimension box or infinite potential well

Description of Orthogonality of the wave functions of a particle in one dimension box or infinite potential well:

Let $\psi_{n}(x)$ and $\psi_{m}(x)$ be the normalized wave functions of a particle in the interval $(0, L)$ corresponding to the different energy level $E_{n}$ and $E_{m}$ respectively. These wave functions are:

$\psi_{n}(x)= \sqrt{\frac{2}{L}} sin \frac{n \pi x}{L}$

$\psi_{m}(x)= \sqrt{\frac{2}{L}} sin \frac{m \pi x}{L}$

Where $m$ and $n$ are integers.

In this function are real. Therefore

$\psi_{n}^{*}(x) = \psi_{n}(x)$

$\psi_{m}^{*}(x) = \psi_{m}(x)$

Where $m=n$,

$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx = \frac{2}{L} \int_{0}^{L} sin \frac{m \pi x}{L} . sin \frac{n \pi x}{L} dx$

$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx =\frac{1}{L} \int_{0}^{L} \left[ cos \left\{ \frac{(m-n) \pi x}{L} \right\} - cos \left\{ \frac{(m+n) \pi x}{L} \right\} \right] dx $

$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx =\frac{1}{L} \left[ \frac{L}{\pi(m-n)} sin \left\{ \frac{(m-n) \pi x}{L} \right\} - \frac{L}{\pi(m+n)} sin \left\{ \frac{(m+n) \pi x}{L} \right\} \right]_{0}^{L} $

$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx =\frac{1}{L} \left[ \frac{L}{\pi(m-n)} sin \left\{ \frac{(m-n) \pi x}{L} \right\} - \frac{L}{\pi(m+n)} sin \left\{ \frac{(m+n) \pi x}{L} \right\} \right]_{0}^{L} $

$\int_{0}^{L} \psi_{n}^{*}(x) \psi_{m}^{*}(x) dx =0$

Hence, The function is mutually orthogonal in the interval $(0, L)$. These functions $\psi_{n}(x)$ and $\psi_{m}(x)$ are also normalized in this interval. The wave function, which is normalized and mutually orthogonal in an interval is said to form an orthogonal set in this interval. Since the wave function are zero outside the interval $(0, L)$, they are also orthogonal wave function in the whole range of $x$ axis in the interval $(-\infty, +\infty)$.

Read More

The electric potential at different points (like on the axis, equatorial, and at any other point) of the electric dipole

Electric Potential due to an Electric Dipole:

The electric potential due to an electric dipole can be measured at different points:

1. The electric potential on the axis of the electric dipole


2. The electric potential on the equatorial line of the electric dipole


3. The electric potential at any point of the electric dipole

1. The electric potential on the axis of the electric dipole:

Let us consider, An electric dipole AB made up of two charges of -q and +q coulomb is placed in a vacuum or air at a very small distance of $2l$. Let a point $P$ is on the axis of an electric dipole and place at a distance $r$ from the center point $O$ of the electric dipole. Now put the test charged particle $q_{0}$ at point $P$ for the measurement of electric potential due to dipole's charges.

So Electric potential at point $P$ due $+q$ charge of electric dipole→

$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{r-l}$

The electric potential at point $P$ due $-q$ charge of electric dipole→

$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{r+l}$

Electric potential is a scalar quantity. Hence the resultant potential $V$ at the point $P$ will be the algebraic sum of the potential $V_{+q}$ and $V_{-q}$. i.e. →

$ V=V_{+q}+V_{-q}$

Now substitute the value of $V_{+q}$ and $V_{-q}$ in the above equation →

$ V= \frac{1}{4\pi \epsilon_{0}} \frac{q}{r-l} -\frac{1}{4\pi \epsilon_{0}} \frac{q}{r+l}$

$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{q}{r-l} - \frac{q}{r+l} \right]$

$ V= \frac{q}{4\pi \epsilon_{0}} \left[ \frac{1}{r-l} - \frac{1}{r+l} \right]$

$ V= \frac{q}{4\pi \epsilon_{0}} \left[ \frac{ \left( r+l \right)-\left (r-l \right)}{r^{2}-l^{2}} \right]$

$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{2ql}{r^{2}-l^{2}} \right]$

$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{p}{r^{2}-l^{2}} \right] \qquad \left( \because p=2ql\right)$

If $r$ is much larger then $2l$. So $l^{2}$ can be neglected in comparison to $r^{2}$. Therefore electric potential at the point $P$ due to the electric dipole is →

$ V= \frac{1}{4\pi \epsilon_{0}} \left[ \frac{p}{r^{2}} \right] $

2. The electric potential on the equatorial line of the electric dipole:

Let us consider, An electric dipole AB made up of two charges of $+q$ and $-q$ coulomb are placed in vacuum or air at a very small distance of $2l$. Let a point $P$ be on the equatorial line of an electric dipole and place it at a distance $r$ from the center point $O$ of the electric dipole. Now put the test charged particle $q_{0}$ at point $P$ for the measurement of electric potential due to dipole's charges.

So Electric potential at point $P$ due $+q$ charge of electric dipole→

$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{BP}$

$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}}$

The electric potential at point $P$ due $-q$ charge of electric dipole→

$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{AP}$

$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}}$

$\therefore$ The resultant potential at point $P$ is

$ V=V_{+q}+V_{-q}$

$ V=\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}}-\frac{1}{4\pi \epsilon_{0}} \frac{q}{\sqrt{r^{2}+l^{2}}} $

$V=0 $

Thus, the electric potential is zero on the equatorial line of a dipole (but the intensity is not zero). So No work is done in moving a charge along this line.

3. The electric potential at any point of the electric dipole:

Let us consider, an electric dipole $AB$ of length $2l$ consisting of the charge $+q$ and $-q$. Let's take a point $P$ in general and its distance is $r$ from the center point $O$ of the electric dipole AB.

Let the distance of point $P$ from the point $A$ and Point $B$ of the dipole is $PB=r_{1}$ and $PA=r_{2}$ respectively.

So, The electric potential at point $P$ due to the $+q$ charge of the electric dipole is →

$ V_{+q}=\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{1}}$

$ V_{-q}=-\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{2}}$

The resultant potential at point $P$ is the algebraic sum of potential due to charges $+q$ and $-q$ of the dipole. That is

$ V=V_{+q}+V_{-q}$

$ V=\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{1}}-\frac{1}{4\pi \epsilon_{0}} \frac{q}{r_{2}}$

$ V=\frac{1}{4\pi \epsilon_{0}} \left(\frac{q}{r_{1}}-\frac{q}{r_{2}} \right) \qquad(1)$        

Now simplify the above equation by applying the Geometry from the figure. i.e. From the figure, Acute angle $\angle POB$, we can write as,

$ r^{2}_{1}=r^{2}+l^{2}-2rlcos\theta \qquad(2)$

$ r^{2}_{2}=r^{2}+l^{2}-2rlcos \left(\pi - \theta \right)$

$ r^{2}_{2}=r^{2}+l^{2}+2rlcos \theta \qquad(3)$

The equation $(2)$ may be expressed as →

$ r^{2}_{1}=r^{2} \left[1+ \frac{l^{2}}{r^{2}}-\frac{2l}{r}cos\theta \right] $

Taking distance $r$ much greater than the length of dipole (i.e. r>>l), so we may retain only first order term in $\frac{l}{r}$,

$ \therefore r^{2}_{1}=r^{2} \left[1- \frac{2l}{r}cos\theta \right]$

$ r_{1}=r \left[1- \frac{2l}{r}cos\theta \right]^{\frac{1}{2}}$

$ \frac {1}{r_{1}}=\frac{1}{r} \left[1- \frac{2l}{r}cos\theta \right]^{-\frac{1}{2}}$

Now applying the binomial theorem in the above equation. So we get $ \frac {1}{r_{1}}=\frac{1}{r} \left[1+ \frac{l}{r}cos\theta \right]$

Similarly,

$ \frac {1}{r_{2}}=\frac{1}{r} \left[1- \frac{l}{r}cos\theta \right]$

Substituting these values in equation $(1)$, we get

$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{q}{r} \left(1+ \frac{l}{r}cos\theta \right)-\frac{q}{r} \left(1- \frac{l}{r}cos\theta \right) \right]$

$ V=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r} \left[ \left(1+ \frac{l}{r}cos\theta \right)- \left(1- \frac{l}{r}cos\theta \right) \right]$

$ V=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r} \left[ \left(1+ \frac{l}{r}cos\theta \right)- \left(1- \frac{l}{r}cos\theta \right) \right]$

$ V=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r} \left[ \frac{2l cos\theta}{r}\right]$

$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{2ql cos\theta}{r^{2}}\right]$

But $q\times 2l=p$ (dipole moment)

$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{p cos\theta}{r^{2}}\right]$

The vector form of the above equation can be written as →

$ V=\frac{1}{4\pi\epsilon_{0}} \left[ \frac{\overrightarrow{p} \cdot \overrightarrow{r} }{r^{2}}\right]$

The above two equations hold only under the approximation that the distance of observation point $P$ is much greater than the size of the dipole.

Special Case:   

1. At axial points $\theta=0^{\circ}$,
   
   
   then $cos\theta= cos 0^{\circ}=1$,
   
   
   Therefore, $ V=\frac{1}{4\pi\epsilon_{0}} \frac{p}{r^{2}}$
  
2. At equatorial points $\theta=90^{\circ}$,
   
   
   then $cos\theta= cos 90^{\circ}=0$,
   
   
   Therefore,$ \quad V=0$

Now comparing this result with the potential due to a point-charge, we see that:     

1. In a fixed direction, that is , fixed $\theta$, $V\propto \frac{1}{r^{2}}$. here rather than $V \propto \frac{1}{r}$;
  
2. Even for a fixed distance $r$, there is now a dependence on direction, that is, on $\theta$.

Read More